[深度学习]卷积神经网络(CNN)
1.卷积神经网络CNN
1.1卷积神经网络的概念
CNN(Convolutional Neural Networks, ConvNets, 卷积神经网络)是神经网络的一种,是理解图像内容的最佳学习算法之一,并且在图像分割、分类、检测和检索相关任务中表现出色。
卷积是数学分析中的一种积分变换的方法,在图像处理中采用的是卷积的离散形式。对于图像操作来说,使用互相关运算作为卷积的基础计算方式。
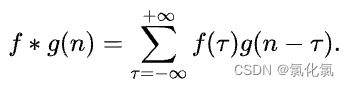
具体可以参考传送门
1.2为什么需要卷积
在入门深度学习之前,最先接触到的神经网络模型应该是全连接。那如果对一张图片(224*224)使用全连接的方式进行训练,假设其隐藏层有100个神经元,其参数量量为:
224 ∗ 224 ∗ 100 = 5017600 \\224*224*100=5017600\\ 224∗224∗100=5017600
全连接需要我们将一张图片展开成(n,)形状,会破环这张图片的空间信息
但如果我们使用卷积神经网络,其卷积核为5×5,卷积一次后参数量为25,图像大小为220*220,再用全连接计算得到参数量为
220 ∗ 220 ∗ 100 + 25 = 4840025 \\220*220*100+25=4840025\\ 220∗220∗100+25=4840025
但卷积层内部的卷积核不只有一个,通常由多个卷积核组合起来,每个卷积核的每个元素都对应一个权重系数核一个偏差量。对图片进行卷积操作就是把卷积核与原图片做点积操作,可以理解为相似度的比较,每个卷积核就为网络学习到的特征。打个比方,判断一张图片是否为车子,它的底层特征为像素。假设我们的卷积模型设置了10个核,它们的特征可能代表[颜色,形状,轱辘,车窗,方向盘,人…]等待,通过核在原图上进行匹配进而综合判断该图片是否为车子。
实际上,深度卷积神经网络就是去求解这千千万万个核的这么一种网络。这些核不是凭借我们的经验随便定义的,而是通过不断的学习更新得来的,深度卷积神经网络就是不断地去学习,最终求得这些核。而神经网络的不易解释性就在于此,随着模型的复杂,抽象出的核千千万万,我们难以去解释每个核的具体含义,也难以介绍每个中间层和中间结点的含义
2.卷积的运算
2.1卷积核(Kernel)
以二维为例,给定一个图像:X ∈ R^{M×N}
给定一个图像:X ∈ R^{M×N},和一个卷积核:
W∈ R^{U×V},卷积计算公式为

卷积运算是指以一定间隔滑动卷积核的窗口,将各个位置上卷积核的元素和输入的对应元素相乘,然后再求和(有时将这个计算称为乘积累加运算),将这个结果保存到输出的对应位置。卷积运算如下所示:![[深度学习]卷积神经网络(CNN)_第1张图片](http://img.e-com-net.com/image/info8/cb15184bc6ce449690d8c5f69c39a8aa.jpg)
经过卷积之后图像尺寸变小,卷积输出特征图大小:
![[深度学习]卷积神经网络(CNN)_第2张图片](http://img.e-com-net.com/image/info8/2dbd2294e5724343b7dc9bf97da06e70.jpg)
2.2 填充(Padding)
在使用pytorch的时候,定义一个卷积层使用nn.Conv2d(),我们看到其超参数中有个padding=,通常这个参数的值设置为0,1,2。那这个参数到底有什么用呢?
在进行卷积层的处理之前,有时候要向输入数据的周围填入固定的数据(比如0),使用填充的目的是使输出尺寸和输入尺寸保持一致。如果不调整尺寸,经过多次卷积之后,输出尺寸会变得很小,导致边缘信息丢失,所以进行填充,也让每个输入方块都能作为卷积窗口的中心
注意,padding填的0,1,2,指的是在输入尺寸周围填充多少圈,而不是指填充的数值
o u t out out=[( n h n_h nh- k h k_h kh+ 2 p h 2p_h 2ph+1), ( n w n_w nw- k w k_w kw+ 2 p w 2p_w 2pw+1)]
p p p通常取(k-1)/2 (此时输出大小和输入大小相同)
例如:一个尺寸5*5的特征图,卷积核大小为3*3,若想保持输出大小不变,需要填充值为多少?
答:padding=(k-1)/2=1
上图gif即为此题解释。
2.3 步幅(stride)
步幅是设置nn.Conv2d()的另一个重要参数,其作用就是卷积核在输入特征图的采样间隔。但这有什么用呢?不妨让我们先引出这一个问题
例如:给定输入大小224*224,在使用5*5卷积核的情况下,需要多少层才能降到4*4呢?
答:55次,这样的权重数将会为55*5*5.
显然这样的计算量是我们不想要的,那么如何减少计算量呢?这就是stride的目的。如下图是stride=2的卷积核计算过程。![[深度学习]卷积神经网络(CNN)_第4张图片](http://img.e-com-net.com/image/info8/58cf0ad8a7ab48b1ac0eaf7979f39746.gif)
其输出特征图大小计算公式为:
o u t = ( n − k + s ) s out=\frac{(n-k+s)}{s} out=s(n−k+s)
2.4 总结
综合上面三个超参数,我们常使用的的输出特征计算公式:
o u t = ( n + 2 p − k + s ) s out=\frac{(n+2p-k+s)}{s} out=s(n+2p−k+s)
三个重要超参数总结:
卷积核大小(kernel_size):小卷积核比大卷积核能减少卷积参数,增强网络容量和复杂度.常使用的卷积核和大小为3*3,5*5
填充(padding):使输出特征图大小与输入相同,每个输入方块都作为卷积窗口的中心
步幅(stride):减少输入参数的数目,减少计算量
3.pytorch代码讲解
基础的讲解可以看看这两篇blog传送门1和c传送门2
以下内容为一些拓展部分
3.1 卷积的权重
torch.nn.Conv2d在函数调用后会自动初始化卷积核的weight和偏置bias。查看及修改weight,bias的方法
import torch
from torch import nn
#这里已将weight和bias初始化
conv = nn.Conv2d(in_channels=2,out_channels=1,kernel_size=3)
conv.weight, conv.bias
#(Parameter containing:
tensor([[[[ 0.0569, 0.1721, 0.1553],
[ 0.1638, 0.1793, 0.0428],
[ 0.1925, 0.1297, 0.0609]],
[[ 0.0363, 0.1484, 0.1257],
[ 0.0374, 0.0282, -0.1510],
[ 0.1836, 0.0151, 0.1023]]]], requires_grad=True),
Parameter containing:
tensor([-0.1692], requires_grad=True))
#
#手动设定
#获取conv.weight.data以及conv.bias.data属性,后续调用torch.tensor的不同方法即可进行修改
conv.weight.data.zero_(),conv.bias.data.zero_()
#
(Parameter containing:
tensor([[[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]]]], requires_grad=True),
Parameter containing:
tensor([0.], requires_grad=True))
#
3.2 padding_mode
padding一般情况下,卷积核的大小是奇数,为了使得图像边缘的像素也要参与卷积计算,就需要在图像or特征图的边缘进行填充,padding指定为几,则会填充几行的数。具体的填充数由填充方式决定(padding_mode),填充方式有constant(常量填充,默认情况下是0填充),reflect(反射填充)、replicate(复制填充)、circular(循环填充)
3.2.1 zeros填充
在输入特征图周围填充一层0。
x = torch.reshape(torch.range(1,48),(1,3,4,4))
x
#tensor([[[[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.],
[13., 14., 15., 16.]],
[[17., 18., 19., 20.],
[21., 22., 23., 24.],
[25., 26., 27., 28.],
[29., 30., 31., 32.]],
[[33., 34., 35., 36.],
[37., 38., 39., 40.],
[41., 42., 43., 44.],
[45., 46., 47., 48.]]]])
#
conv = nn.Conv2d(3,3,1,stride=1,padding=1,padding_mode='zeros')
out = conv(x)
out
#
tensor([[[[ 0.4905, 0.4905, 0.4905, 0.4905, 0.4905, 0.4905],
[ 0.4905, -5.4124, -5.3716, -5.3307, -5.2899, 0.4905],
[ 0.4905, -5.2490, -5.2082, -5.1673, -5.1265, 0.4905],
[ 0.4905, -5.0857, -5.0448, -5.0040, -4.9631, 0.4905],
[ 0.4905, -4.9223, -4.8814, -4.8406, -4.7997, 0.4905],
[ 0.4905, 0.4905, 0.4905, 0.4905, 0.4905, 0.4905]],
[[-0.3463, -0.3463, -0.3463, -0.3463, -0.3463, -0.3463],
[-0.3463, -3.3164, -3.3875, -3.4586, -3.5297, -0.3463],
[-0.3463, -3.6008, -3.6719, -3.7430, -3.8141, -0.3463],
[-0.3463, -3.8852, -3.9563, -4.0274, -4.0984, -0.3463],
[-0.3463, -4.1695, -4.2406, -4.3117, -4.3828, -0.3463],
[-0.3463, -0.3463, -0.3463, -0.3463, -0.3463, -0.3463]],
[[-0.5141, -0.5141, -0.5141, -0.5141, -0.5141, -0.5141],
[-0.5141, 0.9534, 0.7417, 0.5301, 0.3184, -0.5141],
[-0.5141, 0.1068, -0.1049, -0.3165, -0.5282, -0.5141],
[-0.5141, -0.7398, -0.9515, -1.1631, -1.3748, -0.5141],
[-0.5141, -1.5864, -1.7981, -2.0097, -2.2214, -0.5141],
[-0.5141, -0.5141, -0.5141, -0.5141, -0.5141, -0.5141]]]],
grad_fn=)
#
看out的输出结果,发现每个通道周围一圈的数值都是一样的,但按理来说应该为0.导致这样的结果是因为输入结果给默认加上了偏置bias.
可以用conv.bias查看偏置值或初始定义conv =nn.Conv2d(3,3,1,stride=1,padding=1,padding_mode='zeros',bias=False)删除偏置.
re = out-conv.bias.reshape(3,1,1)
print(re)
#
tensor([[[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 7.5260, 8.3309, 9.1359, 9.9408, 0.0000],
[ 0.0000, 10.7457, 11.5507, 12.3556, 13.1605, 0.0000],
[ 0.0000, 13.9654, 14.7704, 15.5753, 16.3802, 0.0000],
[ 0.0000, 17.1852, 17.9901, 18.7950, 19.5999, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
[[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 4.3597, 4.7229, 5.0861, 5.4493, 0.0000],
[ 0.0000, 5.8126, 6.1758, 6.5390, 6.9022, 0.0000],
[ 0.0000, 7.2654, 7.6286, 7.9918, 8.3550, 0.0000],
[ 0.0000, 8.7182, 9.0814, 9.4446, 9.8078, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
[[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, -9.0218, -8.9538, -8.8858, -8.8178, 0.0000],
[ 0.0000, -8.7497, -8.6817, -8.6137, -8.5456, 0.0000],
[ 0.0000, -8.4776, -8.4096, -8.3415, -8.2735, 0.0000],
[ 0.0000, -8.2055, -8.1374, -8.0694, -8.0014, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]],
grad_fn=)
#
3.2.2 reflect(反射填充)
conv = nn.Conv2d(3,3,1,stride=1,padding=1,padding_mode='reflect',bias=False)
conv.weight.data = torch.ones(3,3,1,1)
out = conv(x)
out
3.2.3 replicate(复制填充)
3.2.4 circular(循环填充)
3.3 如何搭建CNN神经网络
!!!这部分很重要
搭建网络主要框架:
- 定义模型函数(nn.Module)
- 定义网络层,通常格式为卷积-激活层-池化层 (激活层与池化层后续文章会介绍)
- 前向传播 forward将前面网络贯彻
class CNN(nn.Module):
def __init__(self):
super(CNN,self).__init__()
# 输入为[1,28,28]
self.conv1 = nn.Sequential(
nn.Conv2d(in_channels=1,out_channels=16,kernel_size=3,padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2)
)
# [16,14,14]
self.conv2 = nn.Sequential(
nn.Conv2d(in_channels=16,out_channels=32,kernel_size=3,padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2)
)
#[32,7,7]
self.output = nn.Linear(in_features=32*7*7,out_features=10)
def forward(self,x):
x = self.conv1(x)
x = self.conv2(x)
x = x.view(x.size(0),-1) # 保留batch,将后面的乘在一起
x = self.output(x)
return x
以手写数字识别为例
import torchvision
import torch.utils.data as Data
from torch.utils.data import DataLoader
# 定义参数
learing_rate=1e-3
epoches=10
batch_size = 64
# 下载训练集和测试集
train_data = torchvision.datasets.MNIST(
root = "./dataset/mnist",
train=True, # True为下载训练数据集,False为下载测试数据集
transform = torchvision.transforms.ToTensor(), # 将PIL,Image从(H*W*C)转为(C*H*W)的tensor,并归一化
download=True
)
test_data = torchvision.datasets.MNIST(
root = "./dataset/mnist",
train=False,
transform = torchvision.transforms.ToTensor(), # 将PIL,Image从(H*W*C)转为(C*H*W)的tensor,并归一化
download=True
)
# 构建DataLoader
train_loader = DataLoader(dataset=train_data,batch_size=batch_size,shuffle=True,num_workers=3)
test_loader = DataLoader(dataset=test_data,batch_size=batch_size,shuffle=False,num_workers=3)
2.定义优化器optimizer=torch.optim.xxx(net.parameters(),lr=xxx),
3.再定义损失函数(自己写class或者直接用官方的,loss_function=nn.CrossEntropyLoss()或者其他。
4.在定义完之后,开始一次一次的循环:
①先清空优化器里的梯度信息,opt.zero_grad();
②再将input传入,output=net(input) ,正向传播
③算损失,loss=loss_function(target,output) ##这里target就是参考标准值GT,需要自己准备,和之前传入的input一一对应
④误差反向传播,loss.backward()
⑤更新参数,optimizer.step()
# 模型训练
cnn = CNN()
# 定义优化器和损失函数
optimizer = torch.optim.Adam(cnn.parameters(),lr=learing_rate)
loss_function = nn.CrossEntropyLoss()
# 开始训练
for epoch in range(epoches):
print("进行第{}个epoch".format(epoch))
running_loss = 0.
running_acc = 0.
for step,(img,label) in enumerate(train_loader):
predict = cnn(img)
loss = loss_function(predict,label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if step % 50 == 0:
count=0
correct_num=0
acc=0
for step,(img,label) in enumerate(test_loader):
test_predict = cnn(img)
pred_y = torch.max(test_predict,1)[1]
correct_num = (pred_y==label).sum().item() # 将tensor转int
acc += correct_num
count+=len(label)
acc_rate = acc/count
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % acc_rate)
![[深度学习]卷积神经网络(CNN)_第3张图片](http://img.e-com-net.com/image/info8/df34027d354c4551be5dea89904c1024.gif)
![[深度学习]卷积神经网络(CNN)_第5张图片](http://img.e-com-net.com/image/info8/2ce73052202d4c899c7fa14ec667df90.jpg)
![[深度学习]卷积神经网络(CNN)_第6张图片](http://img.e-com-net.com/image/info8/9e750fc78e11471dad740daf1f3181ec.jpg)
![[深度学习]卷积神经网络(CNN)_第7张图片](http://img.e-com-net.com/image/info8/1f8f7daa0a5749ee9fc418b0c0606641.jpg)