GAMES101笔记 Lecture03 Transformation

Transoformation(变换)

Why stuty transformation(为什么要学习变换呢?)

2D transformations(2D变换)

Scale transformation(缩放变换)

写成数学形式：
$x^{\prime }=sx$
$y^{\prime }=sy$
在这里，$s=0.5$。
写成矩阵形式，结果如下：
$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$

在这里，我们称矩阵$\left[\begin{array}{ll}s& 0\\ 0& s\end{array}\right]$为缩放矩阵。
如果缩放不是均匀的：

此时变换可以写成如下形式：
$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}{s}_x& 0\\ 0& s_y\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$

缩放矩阵：$\left[\begin{array}{ll}{s}_x& 0\\ 0& s_y\end{array}\right]$

Reflection Matrix(反射矩阵)

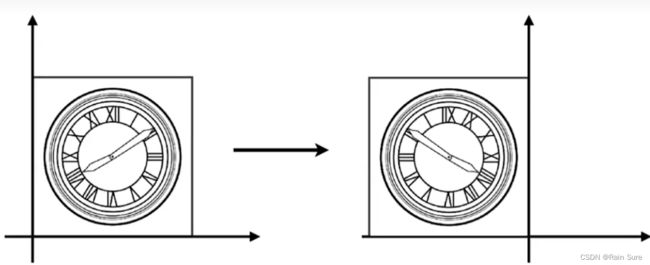
坐标变换$x^{\prime }=-x,y^{\prime }=y$

Shear Matrix(切变矩阵)

提示：

• 竖直方向上的位移始终为$0$；
• 当$y=0$时，水平方向的位移为$0$；
• 当$y=1$时，水平方向位移是$a$；

变换方程为：$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$

Rotate transformation(旋转变换)

默认是绕着原点$(0,0)$，逆时针旋转。

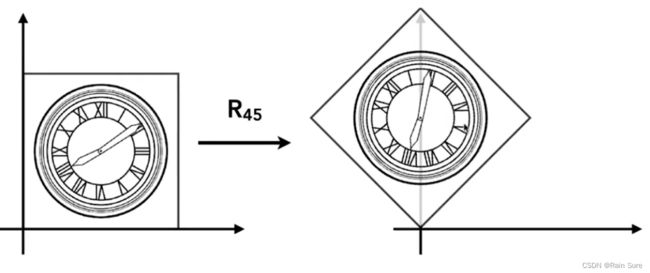
逆时针旋转角度$\theta$的旋转矩阵如下：
$R_{\theta }=\left[\begin{array}{ll}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$

Linear Transforms = Matrices(线性变换 = 矩阵)

通过上面几个变换的例子，我们发现无论哪种变换，我们均可以写成矩阵的形式，因为它们都是线性变换：
$x^{\prime }=ax+by$
$y^{\prime }=cx+dy$

变换方程如下：

$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$

Homogeneous coordinates(齐次坐标)

Translation(平移) 引入齐次坐标

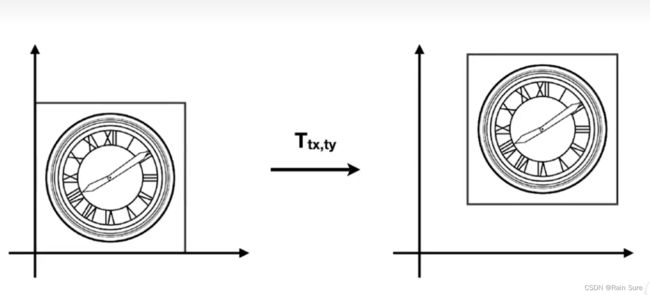
平移变换就不好写成两个矩阵相乘的形式，只能写成下面的形式：
$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]+\left[\begin{array}{l}{t}_x\\ t_y\end{array}\right]$

因为，平移操作并不属于线性变换。

但是，我们并不希望将平移当作一种特殊的情况考虑。
有没有一种特殊方式来表示全部变换呢？

Solution: Homogenous Coordinates(解决方法：齐次坐标)

添加一个新的维度：

• 2D point = $(x,y,1{)}^T$
• 2D vector = $(x,y,0{)}^T$

现在使用矩阵来表示平移变换，变换方程如下：
[ x ′ y ′ w ′ ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y 1 ] = [ x + t x y + t y 1 ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ w^{\prime} \end{array}\right]=\left[\begin{array}{ll} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{l} x + t_{x} \\ y + t_{y} \\ 1 \end{array}\right] ​x′y′w′​ ​= ​100​010​tx​ty​1​ ​ ​xy1​ ​= ​x+tx​y+ty​1​ ​

向量具有平移不变性，这就是为什么向量的第三维是$0$，可以有效地保证其在平移时保持不变。

[ x y w ] \left[\begin{array}{l} x \\ y \\ w \end{array}\right] ​xyw​ ​ 表示的点都是 [ x / w y / w 1 ] , w ≠ 0 \left[\begin{array}{l} x / w \\ y / w \\ 1 \end{array}\right], w\ne0 ​x/wy/w1​ ​,w=0。

在齐次坐标下，合法的操作：

• vector + vector = vector
• point - point = vector
• point + vector = point
• point + point = 两个点的中点

Affine Transformations(仿射变换)

放射变换等于线性变换加上一次平移变换

$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]+\left[\begin{array}{l}{t}_x\\ t_y\end{array}\right]$

使用齐次坐标，变换方程如下：
[ x ′ y ′ w ′ ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y 1 ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ w^{\prime} \end{array}\right]=\left[\begin{array}{ll} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] ​x′y′w′​ ​= ​100​010​tx​ty​1​ ​ ​xy1​ ​

现在可以使用一个方程来表示全部变换了，唯一的代价就是多了一维，增加了空间。

Inverse Transform(逆变换)

变换矩阵$M$的逆矩阵$M^{-1}$在几何意义下也是逆变换。

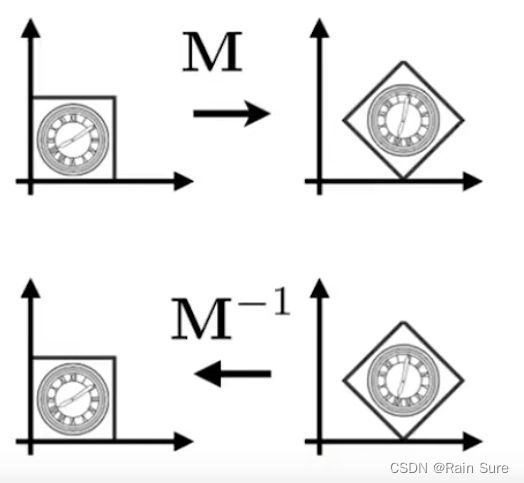
Composing Transforms(组合变换)

变换的顺序是影响最后的结果的，因为矩阵乘法不满足交换律。

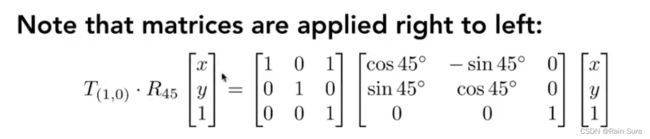
变换矩阵是从右到左进行应用的。

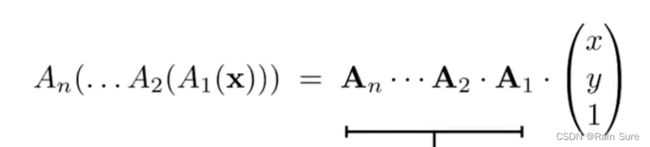
Decomposing Complex Transforms(分解复杂的变换)

如果绕着一个指定的顶点$c$进行旋转：

1. 首先将中心移动到原点。
2. 旋转。
3. 再将其移动回原来的位置。

变换表示如下：
$T(c)\ast R(\alpha )\ast T(-c)$

3D Transforms(三维的变换)

使用齐次坐标进行表示：

• 3D point = $(x.y,z,1{)}^T$
• 3D vector = $(x,y,z,0{)}^T$

$(x,y,z,w)(w\ne 0)$，表示的点为$(x/w,y/w,z/w)$

使用下面$4\times 4$的矩阵来进行仿射变换：
( x ′ y ′ z ′ 1 ) = ( a b c t x d e f t y g h i t z 0 0 0 1 ) ⋅ ( x y z 1 ) \left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{lllc} a & b & c & t_{x} \\ d & e & f & t_{y} \\ g & h & i & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right) ​x′y′z′1​ ​= ​adg0​beh0​cfi0​tx​ty​tz​1​ ​⋅ ​xyz1​ ​

参考资源

GMAES101 Lecture03