CNN卷积神经网络实现手写数字识别（基于tensorflow）

1.1卷积神经网络简介

卷积网络的核心思想是将：
局部感受野
权值共享（或者权值复制）
时间或空间亚采样

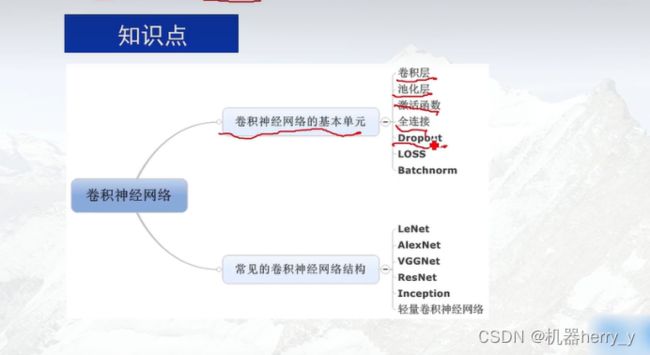
卷积神经网络（Convolutional Neural Networks，简称：CNN）是深度学习当中一个非常重要的神经网络结构。它主要用于用在图像图片处理，视频处理，音频处理以及自然语言处理等等。

早在上世纪80年代左右，卷积神经网络的概念就已经被提出来了。但其真正的崛起却是在21世纪之后，21世纪之后，随着深度学习理论的不断完善，同时，由计算机硬件性能的提升，计算机算力的不断发展，给卷积神经网络这种算法提供了应用的空间。著名的AlphaGo，手机上的人脸识别，大多数都是采用卷积神经网络。因此可以说，卷积神经网络在如今的深度学习领域，有着举足轻重的作用。

在了解卷积神经网络之前，我们务必要知道：什么是神经网络（Neural Networks），关于这个，我们已经在深度学习简介的 第二部分有所介绍。这里就不赘述了。在了解了神经网络的基础上，我们再来探究：卷积神经网络又是什么呢？当中的“卷积”这个词，又意味着什么呢？

1.2 神经网络

1.2.1 神经元模型

人工神神经网络(neural networks)方面的研究很早就已出现，今天“神经网络” 已是一个相当大的、多学科交叉的学科领域.各相关学科对神经网络的定义多种多样。简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应” 。
神经网络中最基本的成分是神经元(neuron)模型,即上述定义中的“简单单元”，在生物神经网络中,每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阈值”(threshold),那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。在这个模型中，神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值将与神经元的间值进行比较，然后通过激活函数处理，产生神经元输出。

1.2.2 神经网络模型

神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

1.3 卷积神经网络

1.3.1卷积的概念

卷积神经网络与普通神经网络的区别在于，卷积神经网络包含了一个由卷积层和子采样层（池化层） 构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元连接。在CNN的一个卷积层中，通常包含若干个特征图(featureMap)，每个特征图由一些矩形排列的的神经元组成，同一特征图的神经元共享权值，这里共享的权值就是卷积核。卷积核一般以随机小数矩阵的形式初始化，在网络的训练过程中卷积核将学习得到合理的权值。共享权值（卷积核）带来的直接好处是减少网络各层之间的连接，同时又降低了过拟合的风险。子采样也叫做池化（pooling），通常有均值子采样（mean pooling）和最大值子采样（max pooling）两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度，减少了模型的参数。

过滤器图像中，可以看到一些斑块是暗的，而其他斑块是亮的。
像素值的范围从 0 到 255。
0 对应于全黑，255 对应于白色。这意味着暗色块的权重低于亮色块。
当输入图像发生仿射变换时，白块将更负责激活图像的该部分。
当对权重与像素值进行元素乘积时，模型将更多地关注权重值更多的图像区域。


什么是特征图：
当图像像素值经过过滤器后得到的东西就是特征图，也就是说，在卷积层上看到的：图像经过卷积核后的内容，这一操作也就是所谓的卷积操作。
**特征图：**可以看到不同的过滤器在创建图像的特征图时关注不同的方面。
一些特征图专注于图像的背景。
一些特征图专注于图像的轮廓。
一些过滤器会专注于背景较暗但猫的图像较亮的特征图。
这是由于过滤器的相应权重。
从左边图中可以清楚地看出，在深层，神经网络可以看到输入图像的非常详细的特征图

随着图像在各个层中前进，图像中的细节会慢慢消失。它们看起来像噪音，但在这些特征图中肯定有一种人眼无法检测到的模式，但神经网络可以。
当图像到达最后一个卷积层（第 48 层）时，人类不可能分辨出里面有一只猫。但这些最后一层输出对于在卷积神经网络中基本上形成分类层的完全连接的神经元非常重要。

卷积层有很多卷积核，通过做越来越多的卷积，提取到的图像特征会越来越抽象

1.3.2 卷积的计算过程

假设我们输入的是551的图像，中间的那个331是我们定义的一个卷积核（简单来说可以看做一个矩阵形式运算器），通过原始输入图像和卷积核做运算可以得到绿色部分的结果，怎么样的运算呢？实际很简单就是我们看左图中深色部分，处于中间的数字是图像的像素，处于右下角的数字是我们卷积核的数字，只要对应相乘再相加就可以得到结果。例如图

图中最左边的三个输入矩阵就是我们的相当于输入d=3时有三个通道图，每个通道图都有一个属于自己通道的卷积核，我们可以看到输出（output）的只有两个特征图意味着我们设置的输出d=2，有几个输出通道就有几层卷积核（比如图中就有FilterW0和FilterW1），这意味着我们的卷积核数量就是输入d的个数乘以输出d的个数（图中就是2*3=6个），其中每一层通道图的计算与上文中提到的一层计算相同，再把每一个通道输出的输出再加起来就是绿色的输出数字。

1. 卷积层的作用
卷积层的作用是提取输入图片中的信息，这些信息被称为图像特征，这些特征是由图像中的每个像素通过组合或者独立的方式所体现，比如图片的纹理特征，颜色特征。

这里的卷积操作是通过卷积核对每个通道的矩阵从左到右（卷积核一般是3x3的矩阵）从上至下进行互相关运算（先是从左到右，再是从上至下，所以卷积操作也会保留位置信息），就像一个小的窗口一样，从左上角一步步滑动到右下角，滑动的步长是个超参数，互相关运算的意思就是对应位置相乘再相加，最后把三个通道的值也对应加起来得到一个值
2. 池化层的作用
池化层的作用是对卷积层中提取的特征进行挑选，用于减少特征数据量。
常见的池化操作有最大池化和平均池化，池化层是由n×n大小的矩阵窗口滑动来进行计算的，类似于卷积层，只不过不是做互相关运算，而是求n×n大小的矩阵中的最大值、平均值等。
如图，对特征图进行最大池化和平均池化操作：

最大值池化可提取图片纹理，均值池化可保留背景特征

3. 全连接层的作用
池化层的后面一般接着全连接层，全连接层将池化层的所有特征矩阵转化成一维的特征大向量，全连接层一般放在卷积神经网络结构中的最后，用于对图片进行分类，到了全连接层，我们的神经网络就要准备输出结果了，如下图所示，倒数第二列的向量就是全连接层的数据

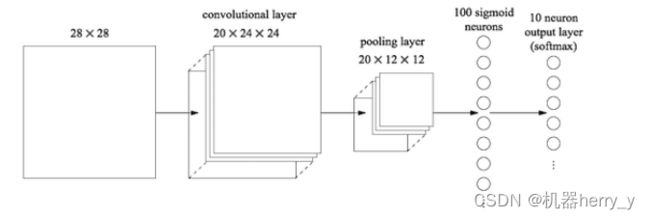
从池化层到全连接层会进行池化操作，数据会进行多到少的映射，进行降维，也就是为什么上图从20×12×12变成100个神经元了，数据在慢慢减少，说明离输出结果越来越近，从全连接层到输出层会再一次减少数据，变成更加低维的向量，这个向量的维度就是需要输出的类别数。然后将这个向量的每个值转换成概率的表示，这个操作一般叫做softmax，softmax使得向量中每个值范围在(0,1)之间，它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。
因为从卷积层过来的数据太多了，全连接层的作用主要是对数据进行降维操作，不然数据骤降到输出层，可能会丢失一些图像特征的重要信息。

1.3.3 感受野

卷积网络在学习过程中保持了图像的空间结构，也就是说最后一层的激活值（feature map）总和原始图像具有空间上的对应关系，具体对应的位置以及大小，可以用感受野来度量。

感受野（Receptive Field）：卷积神经网络各输出层每个像素点在原始图像上的映射区域大小。
下图为感受野示意图：

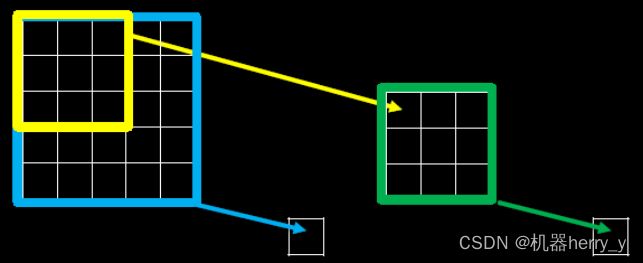
当我们采用尺寸不同的卷积核时，最大的区别就是感受野的大小不同，所以经常会采用多层小卷积核来替换一层大卷积核，在保持感受野相同的情况下减少参数量和计算量。
例如十分常见的用2层3 * 3卷积核来替换1层5 * 5卷积核的方法，如下图所示。

1.3.4 步长和参数量

**步长：**每次卷积核移动的大小。

如何计算卷积核的参数量？

1.4 卷积神经网络的全过程图示

1.5模型训练 与 结果分析(含代码)

可视化分析

**
**

训练次数

模型拟合度

准确率分析

**完整代码：**

import datetime
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import pandas as pd
from sklearn.metrics import precision_score

def image_transform(x_train, x_test):
    # 将28*28图像转成32*32的格式
    x_train = np.pad(x_train, ((0, 0), (2, 2), (2, 2)), 'constant', constant_values=0)
    x_test = np.pad(x_test, ((0, 0), (2, 2), (2, 2)), 'constant', constant_values=0)

    # 数据类型转换 -> 换成tf需要的
    x_train = x_train.astype('float32')
    x_test = x_test.astype('float32')

    # 数据正则化 -> 转换成(0,1)之间
    x_train /= 255
    x_test /= 255

    # 数据维度转换 四维 [n,h,w,c] n -> number, h -> 高度, w -> 宽度, c -> 通道
    x_train = x_train.reshape(x_train.shape[0], 32, 32, 1)
    x_test = x_test.reshape(x_test.shape[0], 32, 32, 1)
    # print(x_test.shape)
    return x_train, x_test

def train_model(x_train, y_train, batch_size, num_epochs):
    '''
    构建模型，训练模型
    返回训练好的模型

    参数：
    ——————————————
    x_trian:训练集
    y_trian:训练集标签
    batch_size:批大小
    num_epochs:训练次数
    filters:卷积核个数
    kernel_size:卷积核大小
    padding:填充方式
    activation：激活函数
    input_shape:输入数据格式
    pool_size：池化大小
    strides:步长
    units：输出的维数
    '''
    model = tf.keras.models.Sequential([
        # 第一卷积层
        tf.keras.layers.Conv2D(filters=36, kernel_size=(5, 5), padding='valid', activation=tf.nn.relu,
                               input_shape=(32, 32, 1)),
        # 第二层池化层 平均池化
        tf.keras.layers.AveragePooling2D(pool_size=(2, 2), strides=(2, 2), padding='same'),
        # 第三层卷积层
        tf.keras.layers.Conv2D(filters=36, kernel_size=(5, 5), padding='valid', activation=tf.nn.relu),
        # 第四层池化层 平均池化
        tf.keras.layers.AveragePooling2D(pool_size=(2, 2), strides=(2, 2), padding='same'),
        # 扁平化层 将多维数据转化一维数据
        tf.keras.layers.Flatten(),
        # 第五层 全连接层  激活函数是relu
        tf.keras.layers.Dense(units=128, activation=tf.nn.relu),
        # Dropout 层 随机舍弃神经元的比例
        tf.keras.layers.Dropout(0.3),
        # 准确率 0.3 => 99.12% 0.5  =>  99.04%
        # 第六层 全连接层  激活函数是relu
        tf.keras.layers.Dense(units=64, activation=tf.nn.relu),
        tf.keras.layers.Dropout(0.3),
        # 第七层 全连接层  激活函数是softmax
        tf.keras.layers.Dense(units=10, activation=tf.nn.softmax)
    ])
    # 优化器
    adam_optimizer = tf.keras.optimizers.Adam(learning_rate, )
    # 编译模型
    model.compile(optimizer=adam_optimizer,
                  loss=tf.keras.losses.sparse_categorical_crossentropy,
                  metrics=['acc'])
    # 模型开始训练
    start_time = datetime.datetime.now()
    # 训练模型
    history = model.fit(x=x_train, y=y_train, batch_size=batch_size, epochs=num_epochs,
                        validation_data=(x_test, y_test))

    # 模型结束训练
    end_time = datetime.datetime.now()
    time_cost = end_time - start_time
    print('时间花费：', time_cost)
    # 检查模型拟合情况
    plt.plot(history.epoch, history.history.get('acc'), label='acc')
    plt.plot(history.epoch, history.history.get('val_acc'), label='val_acc')
    plt.legend()

    return model
if name == '__name__':
    # 定义参数 ：
    num_epochs = 20
    batch_size = 128
    learning_rate = 0.001
    # 检查数据格式
    # print(x_train[0])

    # 读取数据
    data = pd.read_csv('F:\S\\train.csv')
    x_train = data.iloc[:, 1:]
    x_train = np.array(x_train).reshape(42000, 28, 28)
    y_train = np.array(data.iloc[:, 0])
    data1 = pd.read_csv('F:\S\\test.csv')
    x_test = data1.iloc[:, 1:]
    x_test = np.array(x_test).reshape(28000, 28, 28)
    y_test = np.array(data1.iloc[:, 0])
    
    # 数据转换和模型训练
    x_train, x_test = image_transform(x_train, x_test)
    model = train_model(x_train, y_train, batch_size, num_epochs)
    
    # 参数量表
    print(model.summary())
    
    # 预测结果分析
    image_index = 1888
    pred = model.predict(x_test[image_index].reshape(1, 32, 32, 1), )
    print('预测结果', pred.argmax())
    print(model.evaluate(x_test, y_test, verbose=2))
    # 数据可视化
    for i in range(25):
        plt.subplot(5, 5, i + 1)
        plt.imshow(x_test[i].reshape(32, 32))