LeetCode - 15 三数之和
目录
题目来源
题目描述
示例
提示
题目解析
算法源码
题目来源
15. 三数之和 - 力扣(LeetCode)
题目描述
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示
- 3 <= nums.length <= 3000
- -10^5 <= nums[i] <= 10^5
题目解析
本题需要从nums数组中找出所有和为0的三元组,且找出的三元组不能重复。
本题可以分解为两部分逻辑:
- 找到和为0的三元组
- 三元组去重
找和为0的三元组,最简单的方法就是三重for暴力枚举,时间复杂度O(n^3),n = nums.length(),结合备注的nums长度,可以得出暴力法会超时。
因此,我们需要一种更优的算法。
当前最优算法思路为:
首先,将nums数组进行升序,
然后,利用三个指针 i, l, r 来选择三个数,如果i, l,r指针指向的三数之和为0,则找到一个符合要求的三元组。
三指针指向的元素值的大小关系:nums[i] <= nums[l] <= nums[r]
上面三指针的运动逻辑其实可以概括,
首先确定三元组的最小值nums[i],然后找到一个与之匹配的nums[l],nums[r]
这样的话,就将三指针运动 转为了 双指针运动。
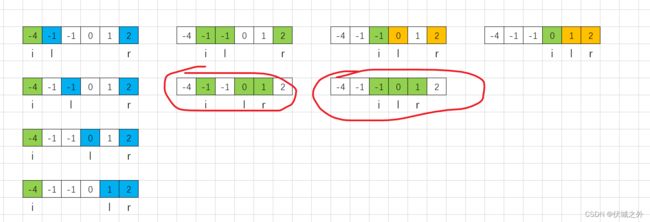
我们通过下面 示例1 图示来理解运动过程:
nums = [-1,0,1,2,-1,-4] 经过升序后,变为nums = [-4,-1,-1,0,1,2]
如上图,我们分别找了:
- 三元组中最小值为-4,即 i 固定指向 0
- 三元组中最小值为-1,即 i 固定指向 1
- 三元组中最小值为-1,即 i 固定指向 2
- 三元组中最小值为0,即 i 固定指向 3
的三元组情况。而针对上面情况,初始时l,r指针固定为:
- l = i + 1
- r = nums.length - 1
由于nums已经升序,因此,如果i, l, r三元组之和sum
- sum > 0,则说明三元组之和大了,我们应该减小它,此时
- i 指针是固定的,因此不能移动 i 指针
- l 指针只能向右移动,因为 l 不能比 i 小,但是 l 指针右移只会增大三元组之和,因此不能移动 l 指针
- r 指针只有向左移动,而 r 指针向左移动的话,会导致nums[r]减少,因此三元组之和也会减少,所以我们左移 r 指针,即r--,可以减少三元组之和
- sum < 0,则说明三元组之和小了,我们应该增大它,此时我们应该右移 l 指针,即 l++,来增大三元组之和
- sum == 0,则说明当前i, l, r指向的三个数就是一个和为0的三元组
上面就是找和为0的三元组的逻辑。
下面就是去重逻辑的实现了
我们通过示例一可以发现,三指针运动过程中,产生了重复的三元组,如下图所示
那么如何才能去重呢?
最简单的方法,其实就是将所有和为0的三元组求出后,对比去重,但是效率非常低,不推荐。
更高效的去重策略是,发现规律,通过上面图示,我们可以发现:
重复的两个三元组,如果基于后面一个来看的话,那么变化的只有 i 指针,且nums[i] == nums[i-1],而l,r位置未发生改变。
如果我们把nums[i]和nums[i-1]看出一个整体的话,那么这两个重复二元组就是同一个。
且他们对于的l,r指针的运动逻辑也是一致的。因此后续会产生重复的二元组。
因此,我们可得去重结论,如果 num[i] == nums[i-1],则后续的l,r指针运动就可以不做了,因为会产生重复的二元组。
如果上面的 i 指针会产生重复二元组外,对于 l, r 指针同样会产生重复二元组。
比如下面例子:
上面例子中,产生了多个重复的三元组
但是实际上,
如果 nums[l] == nums[l+1],则可以直接 l++
如果 nums[r] == nums[r-1],则可以直接 r--
即运动过程如下:
即 nums[l] == nums[l+1] 的话,则 i, l, r 其实和 i, l+1,r 三元组是重复的,因此,我们可以直接跳过l+1的三元组,选择l++
nums[r] == nums[r-1] 的话,则i ,l , r其实和i, l, r-1 三元组是重复的,因此,我们可以直接跳过r-1的三元组,选择r--
另外本题还有一个剪枝优化,
如果 nums[i] > 0的话,由于nums[i]是三元组中最小值,因此nums[i] > 0的话,则nums[l],nums[r]必然也大于0,三元组之和也大于0。
并且nums已经升序,因此nums[i+1]>0也是必然的,即nums[i+1]对应的三元组也是大于0的。
因此如果nums[i] > 0了,则可以直接break掉整个三指针运动。
JS算法源码
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function (nums) {
const ans = [];
nums.sort((a, b) => a - b);
for (let i = 0; i < nums.length - 2; i++) {
// 剪枝
if (nums[i] > 0) break;
// 去重
if (i > 0 && nums[i] == nums[i - 1]) continue;
let l = i + 1;
let r = nums.length - 1;
while (l < r) {
const sum = nums[i] + nums[l] + nums[r];
if (sum > 0) {
r--;
} else if (sum < 0) {
l++;
} else {
ans.push([nums[i], nums[l], nums[r]]);
// 去重
while (l + 1 < r && nums[l] == nums[l + 1]) l++;
// 去重
while (r - 1 > l && nums[r] == nums[r - 1]) r--;
l++;
r--;
}
}
}
return ans;
};
三数之和 - 提交记录 - 力扣(LeetCode)
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
class Solution {
public List> threeSum(int[] nums) {
List> ans = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length - 2; i++) {
// 剪枝优化
if (nums[i] > 0) break;
// 去重
if (i > 0 && nums[i] == nums[i - 1]) continue;
int l = i + 1;
int r = nums.length - 1;
while (l < r) {
int sum = nums[i] + nums[l] + nums[r];
if (sum > 0) {
r--;
} else if (sum < 0) {
l++;
} else {
ArrayList tmp = new ArrayList<>();
Collections.addAll(tmp, nums[i], nums[l], nums[r]);
ans.add(tmp);
// 去重
while (l + 1 < r && nums[l] == nums[l + 1]) l++;
// 去重
while (r - 1 > l && nums[r] == nums[r - 1]) r--;
l++;
r--;
}
}
}
return ans;
}
}
三数之和 - 提交记录 - 力扣(LeetCode)
Python算法源码
class Solution(object):
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
ans = []
nums.sort()
for i in range(len(nums) - 2):
# 剪枝
if nums[i] > 0:
break
# 去重
if i > 0 and nums[i] == nums[i - 1]:
continue
l = i + 1
r = len(nums) - 1
while l < r:
total = nums[i] + nums[l] + nums[r]
if total > 0:
r -= 1
elif total < 0:
l += 1
else:
ans.append([nums[i], nums[l], nums[r]])
# 去重
while l + 1 < r and nums[l] == nums[l + 1]:
l += 1
# 去重
while r - 1 > l and nums[r] == nums[r - 1]:
r -= 1
l += 1
r -= 1
return ans三数之和 - 提交记录 - 力扣(LeetCode)