LeetCode04.寻找两个正序数组的中位数

题目描述：给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。
题目链接
由中位数的性质可知：
奇数的情况：（len+1）/2是中位数 由于向下取整，所以相当于是到len/2+1个数是中位数
偶数的情况：第len/2，len/2+1的平均数是中位数

方法一：合并

算法思想： 合并数组，开辟一个大小为（m+n）/2+1的nums空间，将nums1和nums2有序合并于nums中，对于总数为奇数的，中位数为nums中的最后一个元素，对于总数为偶数的，为nums中倒数第一个和倒数第二个元素的平均数

代码实现：

double findMedianSortedArrays1(vector<int>& nums1, vector<int>& nums2){
    int n1=nums1.size(),n2=nums2.size();
    int len=n1+n2;
    vector<int> nums(len/2+1);
    int p1=0,p2=0;
    for(int i=0;i<nums.size();i++){
   		//放nums1[p1]的情况：1.nums2中的元素都已经放完了  2.当p1未越界并且nums1[p1]
        if(p2>=n2||p1<n1&&nums1[p1]<nums2[p2]){    
            nums[i]=nums1[p1++];
        }
        else if(p1>=n1||p2<n2&&nums2[p2]<=nums1[p1]){
            nums[i]=nums2[p2++];
        }
    }
    if(len%2){
        return nums[len/2];
    }
    else{
        return (nums[len/2]+nums[len/2-1])/2.0;      //除以2.0才会变成小数
    }
}

复杂度： 空间O(M+N) ， 时间：O(M+N)

方法二：依次往后数

算法思想： 和方法一相同，在两个数组中从小到大挨个数，数到中位数，只是不用把数过的数放到数组，减少空间复杂度，用两个变量保存最后得到的中位数就可。

double findMedianSortedArrays2(vector<int>& nums1, vector<int>& nums2) {
    //一个挨着一个数
    //奇数数够(n1+n2)/2个，第(n1+n2)/2+1（m1）返回
    //偶数数够(n1+n2)/2-1,将第(n1+n2)/2（m2）和(n1+n2)/2+1（m1）均值返回
    int n1=nums1.size(),n2=nums2.size();
    int len=n1+n2;
    double m1=-1,m2=-1;  //m2用于记录当是偶数时的第(n1+n2)/2个数
    int p1=0,p2=0;
    for(int i=1;i<=len/2+1;i++){
        m2=m1;
        if(p2>=n2||p1<n1&&nums1[p1]<nums2[p2]){
            m1=nums1[p1++];
        }
        else{
            m1=nums2[p2++];
        }
    }
    if(len%2){
        return m1;
    }
    else{
        return (m1+m2)/2;
    }
}

复杂度： 空间O(1) ， 时间：O(M+N)

方法三：切割数组

算法： 由中位数的特性：以中位数为中心，我们可以将其分为前后元素数目相等的两部分。
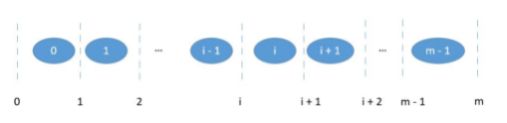
对于一个大小为m数组：可在0~m之间进行切割，当某时的切割刚好可以使得左右元素相等，则找到了中位数。
对于奇数：可以选择找切割完后前边元素多于后边元素一个的位置，中位数就是前边元素的最大值（切割位置的前一个数）
对于偶数：切割完后可使左右两边相等，中位数就为前边部分的最大值和后边元素最小值的平均值。
选择下次的切割位置我们可以用二分法来找，所以对于单个数组找中位数，最终的切割位置可以直接被找到

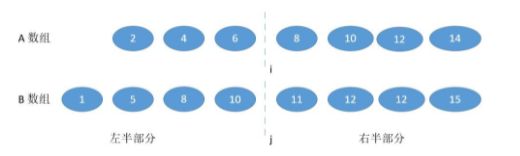
针对本题目在两个数组中找元素，原理相同，在两个数组中分别找切割位置，使得两个数组切割位置的左边元素数目之和等于右边元素数目之和。
在对nums1和nums2分别在i和j之间进行切割：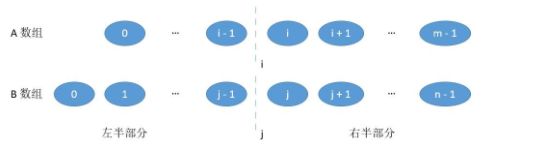
结合中位数的性质，切割位置需满足以下条件：

1. 数目：偶数：i+j=m-i+n-j，奇数：i+j=m-i+n-j+1(左边多一个)
   即：j=(m+n+1)/2-i （偶数加一向下取整相当于没加）
2. 关系：MAX(A[i-1],B[j-1])<=MIN(A[i],B[j])
   由于数组有序，所以本来就有A[i-1]<=A[i]，B[j-1]<=B[j]
   因此条件就变为A[i-1]<=A[i]，B[j-1]<=B[j]
   在开始找切割位置时，我们要保证一直满足数目的条件，因此二分法改变i的值，同时通过公式计算出j，直到满足关系条件。

值得注意的是：在满足等式j=(m+n+1)/2-i时有一个暗含的隐藏条件，i取值在0到m
，j是由j=(m+n+1)/2-i算出的，所以当i取极值（在边界）时，同时也要保证算出来的j不可以越界，即：
当i=0时： 0<= j=(m+n+1)/2 <=n ------>m<=n-1
当i=m时： 0<= j=(m+n+1)/2-m <=n------> m<=n+1
即： m
所以在进行以下处理时，我们要将短的数组作为二分找i的地方，所以当nums1.length>nums2.length时我们要将nums1和nums2换一下位置

在寻找满足条件的切割位置时，可将遇到的场景分为以下四种情况：

1. 当A[i-1]>B[j]时，A的切割位置要向左移，i减小，j增加，为防止越界，在比较时要保证i>0,j

2. 当B[j-1]>A[i]时，A的切割位置要向右移，i增加，j减小，为防止越界，在比较时要保证i0;

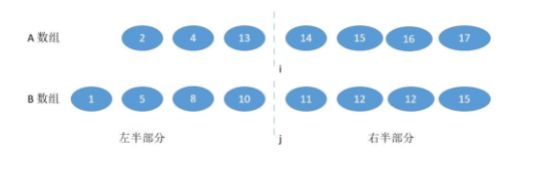
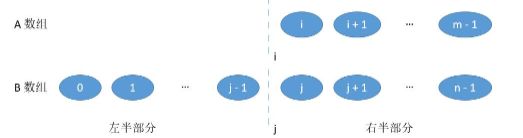
3. 处理最左端边界：即i=0或j=0，即切在了最前面。此时
   当i=0时，左边最大值为B[j-1] ，右边最小值为MIN(A[i],B[j])
   当j=0时，左边最大值为A[i-1]，右边最小值为MIN(A[i],B[j])
   

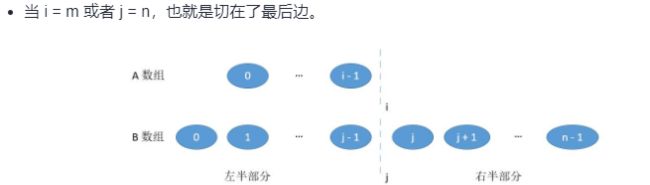
4. 处理右边界：即i=m或j=n，即切在了最后面。此时
   当i=m时，右边最小值为B[j],左边最大值为MAX(A[i-1],B[j-1])
   当j=n时，右边最小值为A[i],左边最大值为MAX(A[i-1],B[j-1])
   

对于循环结束条件：
二分查找结束：即满足关系条件,可以确定下来左边最大值和右边最小值
（和二分结束条件一样，begin>end）

//基于这个思路自己写的菜狗代码
double findMedianSortedArrays3_1(vector<int>& nums1, vector<int>& nums2){
    int m=nums1.size(),n=nums2.size();
    //交换两个数组的处理方式。。RRRR
    if(m>n){
        return findMedianSortedArrays3_1(nums2,nums1);
    }
    int begini=0,endi=m-1;
    int i=(begini+endi+1)/2;
    int j=(m+n+1)/2-i;
    int maxL=-1,minR=-1;

    while(i==0||i==m||j==0||j==n||nums1[i-1]>nums2[j]||nums2[j-1]>nums1[i]){
        //情况1：i要往后，j要往前  防止越界条件：i>0,j
        if(i>0&&j<n&&nums1[i-1]>nums2[j]){
            endi=i-1;
            i=(begini+endi+1)/2;
            j=(m+n+1)/2-i;
        }
            //情况2：i要往前，j要往后  防止越界条件：j>0,i
        else if(i<m&&j>0&&nums2[j-1]>nums1[i]){
            begini=i+1;
            i=(begini+endi+1)/2;
            j=(m+n+1)/2-i;
        }
        //情况3.1：i=0，到达前边界
        if(i==0){
            if((m+n)%2){
                return nums2[j-1];
            }
            else{
                if(j>=n){
                    minR=nums1[0];
                }
                else if(m==0){
                    minR=nums2[j];
                }
                else{
                    minR=min(nums1[0],nums2[j]);
                }

                return (nums2[j-1]+minR)/2.0;
            }
        }
        //情况3.2：j=0，到达前边界
        if(j==0){
            if((m+n)%2){
                return nums1[i-1];
            }
            else{
                if(i>=m){
                    minR=nums2[0];
                }
                else if(n==0){
                    minR=nums1[i];
                }
                else{
                    minR=min(nums2[0],nums1[i]);
                }

                return (nums1[i-1]+minR)/2.0;
            }
        }
        //情况4.1：i=m，到达后边界
        if(i==m){
            maxL=max(nums1[m-1],nums2[j-1]);
            if((m+n)%2){
                return maxL;
            }
            else{
                return (maxL+nums2[j])/2.0;
            }
        }
        //情况4.2：j=n，到达后边界
        if(j==n){
            maxL=max(nums1[i-1],nums2[n-1]);
            if((m+n)%2){
                return maxL;
            }
            else{
                return (maxL+nums1[i])/2.0;
            }
        }


    }
    maxL=max(nums1[i-1],nums2[j-1]);
    minR=min(nums1[i],nums2[j]);
    if((m+n)%2){
        return maxL;
    }
    else{
        return (maxL+minR)/2.0;
    }

}

改良1： 以上代码将不同情况过于分开，导致虽然好理解但是代码非常冗余，因此看了别人的代码后，发现有很多地方是可以合并的。

1. 什么情况下时可以算是找到了中位数的？ 满足关系条件或到达边界
   所以循环体变为三部分（i向后，i向前，找到返回）
2. 左边最大值只有在处理左边界即切在了最前面，情况才会不一样，即当i=0或j=0时,LMax=B[j-1] /A[i-1]；
   右边最小值只有在处理右边界即切在了最后面，情况才会不一样，即当i=m或j=n时，RMin=A[i]/B[j]
3. 无论是奇数还是偶数，都要计算左边最大值。奇数的直接返回，偶数的话继续得右边最小值，再求平均数返回。

double findMedianSortedArrays3_2(vector<int>& nums1, vector<int>& nums2){
    int m=nums1.size(),n=nums2.size();
    if(m>=n){
        return findMedianSortedArrays3_2(nums2,nums1);   
    }
    int begini=0,endi=m;
    int i,j;
    while(begini<=endi) {
        i=(begini+endi+1)/2;
        j=(m+n+1)/2-i;
        //情况1：i要往后，j要往前  防止越界条件：i>0,j
        if (i > 0 && j < n && nums1[i - 1] > nums2[j]) {
            endi = i - 1;
        }
            //情况2：i要往前，j要往后  防止越界条件：j>0,i
        else if (i < m && j > 0 && nums2[j - 1] > nums1[i]) {
            begini = i + 1;
        }
            //情况3.找到+边界
        else {
            int maxL = -1;
            if (i == 0) { maxL = nums2[j - 1]; }
            else if (j == 0) { maxL = nums1[i - 1]; }
            else { maxL = max(nums1[i - 1], nums2[j - 1]); }

            //得出左边最大值后，如果是奇数就可以直接返回了
            if ((m + n) % 2) {
                return maxL;
            }

            int minR = -1;
            if (i == m) { minR = nums2[j]; }
            else if (j == n) { minR = nums1[i]; }
            else { minR = min(nums1[i], nums2[j]); }
            return (maxL + minR) / 2.0;
        }
    }
    return -1;      //力扣要求所有出口都要有返回值，否则也会报错
}

改良二：奇数组变偶数组，合并，加# 让奇数数组变成偶数，可以统一处理。
待完成。。

复杂度： 时间O(log (m+n))，空间O(1)

方法四：转化为在两个数组中寻找第K个小的数问题

基于这个思想，找中位数就变为
对于奇数：找数组中第(m+n)/2+1个小的数
对于偶数：找数组中第(m+n)/2个小的数和第(m+n)/2+1个小的数并求平均数

解决问题：在两个数组中找第K个小的数：
算法：
S1. 分别在A和B两个数组中找下标为begin+k/2-1进行比较，由于他们前面都有k/2-1个数，所以对于A和B中的最小值num，在两个数组标志位的前面最多只有k-2数比num小，所以num包括num所在数组之前的元素肯定都不是第K个元素，所以删掉这些不可能的数
S2. 删掉以后剩下的只有 m+n-(删掉的数目)个元素了,然后在这些书中找第k-(删掉数目)个小的元素
S3. 重复S1 直到K=1

对于删掉的数目讨论：
举个栗子：
对于nums1 {1，2} ，nums2{3，4}
在第一轮中k=2，(k-1)/2=0，则对nums1删掉（(k-1)/2+1个元素
对于nums{1}， nums2{1，2，3，4，5}
在第一轮中k=3，k/2=1,在nums1中这就可能发生越界了。因此我们把比较位置放在数组末尾，删掉也是删掉i-begini+1个元素

double findK(vector<int>& nums1, vector<int>& nums2,int k){
    int m=nums1.size(),n=nums2.size();
    int begini=0,beginj=0;
    int i,j;
    int res;
    while(k!=1){
        if(begini>=m){
            return nums2[beginj+k-1];
        }
        else if(beginj>=n){
            return nums1[begini+k-1];
        }
        i=min(begini+k/2,m)-1;   //为什么是begini+k/2-1 分别举个奇偶的例子就好
        j=min(beginj+k/2,n)-1;
        if(nums1[i]<=nums2[j]){
            k-=i-begini+1;
            begini=i+1;
        }
        else{
            k-=j-beginj+1;
            beginj=j+1;
        }
    }
    //防止k=1，但也遍历到头的情况 如 nums1{}  nums2{1}
    if(begini>=m){
        return nums2[beginj+k-1];
    }
    else if(beginj>=n){
        return nums1[begini+k-1];
    }
    return min(nums1[begini],nums2[beginj]);
}
double findMedianSortedArrays3_1(vector<int>& nums1, vector<int>& nums2){
    int m=nums1.size(),n=nums2.size();
    if((m+n)%2){
        return findK(nums1,nums2,(m+n+1)/2);
    }
    else{
        return (findK(nums1,nums2,(m+n)/2)+findK(nums1,nums2,(m+n)/2+1))/2.0;
    }
}

该方法对边界处理，下标的找寻很困难。多举几个例子。
复杂度： 时间O(log (m+n))，空间O(1)
题解例子多多

总结：
1.解题分步。
2.情况归类减少冗余。
3.本题难在边界情况的处理，要多举例子耐心。
4.算法题每次都不要忘记复杂度的分析