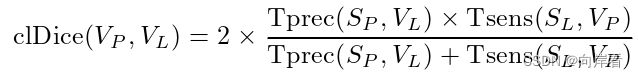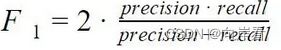clDice-一种新的分割标准-能够促进管状结构分割的连接性

clDice-a Novel Topology-Preserving Loss Function for Tubular StructureSegmentation论文总结

论文：clDice-A Novel Topology-Preserving Loss Function for Tubular Structure

源码：GitHub - jocpae/clDice

目录

一、论文背景和出发点

二、创新点

三、clDice指标

四、clDice的拓扑保证

五、使用clDice训练神经网络

六、Cost函数

七、实验

八、结论

九、代码实现cldice指标

---

一、论文背景和出发点

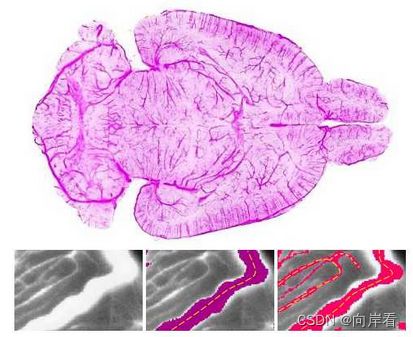
精确分割管状网络状结构，如血管、神经元或道路时，拓扑结构的连通性十分重要，在血管网络的情况下，错过连接的血管会完全改变血流动力学，为了评估这种管状网络结构中的分割，传统的基于体积的性能指标不是最优的。在类似网络拓扑提取的任务中，空间连续的正确体素预测序列比空间体积的正确预测更有意义。

因此本文提出了一种新的相似性度量系数，称为中心线Dice（short-clDice），它是在分割掩模及其（形态学）骨架的截面上计算的。

由上图可见，对于传统dice，这两种不同模型的训练效果达到了相同的数值，可见对于传统dice而言，评价分割管状网络的拓扑结构并不是最优的选择。

二、创新点

作者提出了一种新的连接感知相似性度量clDice，用于基准管状分割算法。作者展示了各种2D和3D网络分割任务的实验结果，以证明提出的相似性测度和损失函数的实际应用性。

三、clDice指标

通过观察，在测量拓扑精度易受假阳性影响，而测量拓扑灵敏度易受假阴性影响。由于希望最大限度地提高精度和灵敏度（recall），于是将clDice定义为两个度量的调和均值（也称之为F1）。

1. Tprec：计算骨架、的分数

Tprec（，）：计算骨架的分数，即拓扑精度。

Tprec（，）：计算骨架的分数，即拓扑灵敏度。对应算子公式如下：

其中，为真值mask，预测分割mask，为从中提取骨架，为从中提取骨架。

2. clDice：计算拓扑精度和拓扑灵敏度的调和均值

cldice算子公式如下：

其中，Tprec（，）为拓扑精度，Tprec（，）为拓扑灵敏度。

cldice是参考F1公式推导而成：

四、clDice的拓扑保证（推理证明）

拓扑保持：某些已存在嵌套包含了对前景和背景的同构等价的暗示，我们称之为拓扑保持。

定理1（同伦等价）：设和是某些单元复合体的连通子复合体。假设上述包含是同伦等价。如果子复形也通过包含和相关，则这些包含也必须是同伦等价。特别地，A和B是同伦等价的。

推论1：设和是两个二进制掩码都包含前景和背景骨架，的前景骨架包含在的前景中，反之亦然，背景也类似。那么和的前景是同伦等价的，它们的背景也是同伦等价的。

clDice的拓扑保证：

当且仅当clDice在(，)的前景和背景上的计算结果均为1时,才满足此推论1中的包含条件。

也就是说，clDice能够证明真值和预测掩码之间的是否具有同伦等价关系，推论出clDice能证明预测掩码是否具有和真值一样的拓扑连接性。

这个证明为clDice作为拓扑保持度量的一般解释奠定了基础。

五、使用clDice训练神经网络

1. 软骨架化（Soft-skeletonization）

目的：为了精确地从mask中提取骨架。

原理：在曲线结构上使用形态学操作（骨架化）进行细化可以保持拓扑结构。最小和最大过滤器（filters）通常用作形态膨胀和腐蚀的灰度替代方案。

方法：提出了“软骨架化”，其中应用迭代最小和最大池化作为形态侵蚀和扩张。算法1如下，描述了其计算中涉及的迭代过程。

其中，算法1中涉及的超参数k，表示迭代次数，必须大于或等于最大观测半径。

软骨骼化的详细步骤如下：

在早期迭代中，半径较小的结构被骨架化并保留，直到后来的迭代中，较厚的结构变为骨架化。这使得能够提取无参数的，被形态驱动的软骨骼。

算法2描述了它的实现。我们称之为soft-clDice。如下图所示：

其中，是来自分段网络的实值概率预测，是真值掩码，表示Hadamard乘积。

六、Cost函数

目的：实现精确分割的同时，保留拓扑结构。

方法：将soft-clDice与soft-Dice结合，得到。对应公式如下：

其中。

soft-cldice能够分割不错的拓扑结构，soft-dice能够分割不错的空间结构，二者结合。

七、实验

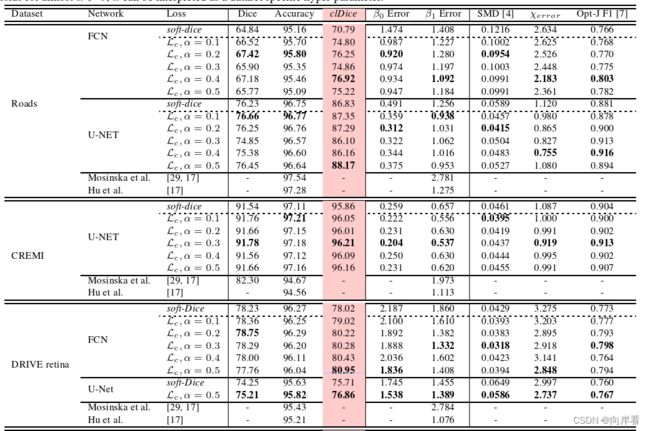
数据集：DRIVE（2D视网膜）、CREMI（3D神经元）。

网络：2D、3D U-Net 和2D、3D FCN。

评估指标：Dice、Accuracy、clDice。

由上图可见，在多种不同的数据集不同的网络中，在中使用soft-cldice训练与soft-dice相比，可以提高Accuracy分数。由此可见soft-cldice指数可以有效的提高分割的精确度。

八、结论

本文介绍了一种新的用于管状结构分割的拓扑保持相似性度量cl-Dice。本文提供了一个理论保证，即clDice同伦等价证明。接下来，在损失函数中使用clDice的可微版本，即soft-clDice，来训练最先进的2D和3D神经网络。我们发现，在soft-clDice上进行训练可以实现具有更准确的连接信息、更好的图相似性、更好的欧拉特性以及改进的Dice和准确性的分割。soft-clDice在计算上是高效的，可以很容易地部署到任何其他基于深度学习的分割任务中，例如生物医学成像中的神经元分割，工业质量控制中的裂纹检测或遥感。

九、代码实现cldice指标

cldice.py

import torch
import torch.nn as nn
from soft_skeleton import soft_skel


class soft_cldice(nn.Module):
    def __init__(self, iter_=3, smooth = 1.):
        super(soft_cldice, self).__init__()
        self.iter = iter_
        self.smooth = smooth

    def forward(self, y_true, y_pred):
        skel_pred = soft_skel(y_pred, self.iter)
        skel_true = soft_skel(y_true, self.iter)
        tprec = (torch.sum(torch.multiply(skel_pred, y_true)[:,1:,...])+self.smooth)/(torch.sum(skel_pred[:,1:,...])+smooth)
        tsens = (torch.sum(torch.multiply(skel_true, y_pred)[:,1:,...])+self.smooth)/(torch.sum(skel_true[:,1:,...])+smooth)
        cl_dice = 1.- 2.0*(tprec*tsens)/(tprec+tsens)
        return cl_dice


def soft_dice(y_true, y_pred):
    """[function to compute dice loss]

    Args:
        y_true ([float32]): [ground truth image]
        y_pred ([float32]): [predicted image]

    Returns:
        [float32]: [loss value]
    """
    smooth = 1
    intersection = torch.sum((y_true * y_pred)[:,1:,...])
    coeff = (2. *  intersection + smooth) / (torch.sum(y_true[:,1:,...]) + torch.sum(y_pred[:,1:,...]) + smooth)
    return (1. - coeff)


class soft_dice_cldice(nn.Module):
    def __init__(self, iter_=3, alpha=0.5, smooth = 1.):
        super(soft_cldice, self).__init__()
        self.iter = iter_
        self.smooth = smooth
        self.alpha = alpha

    def forward(self, y_true, y_pred):
        dice = soft_dice(y_true, y_pred)
        skel_pred = soft_skel(y_pred, self.iter)
        skel_true = soft_skel(y_true, self.iter)
        tprec = (torch.sum(torch.multiply(skel_pred, y_true)[:,1:,...])+self.smooth)/(torch.sum(skel_pred[:,1:,...])+self.smooth)    
        tsens = (torch.sum(torch.multiply(skel_true, y_pred)[:,1:,...])+self.smooth)/(torch.sum(skel_true[:,1:,...])+self.smooth)    
        cl_dice = 1.- 2.0*(tprec*tsens)/(tprec+tsens)
        return (1.0-self.alpha)*dice+self.alpha*cl_dice

 soft_skeleton.py

import torch
import torch.nn as nn
import torch.nn.functional as F


def soft_erode(img):
    if len(img.shape)==4:
        p1 = -F.max_pool2d(-img, (3,1), (1,1), (1,0))
        p2 = -F.max_pool2d(-img, (1,3), (1,1), (0,1))
        return torch.min(p1,p2)
    elif len(img.shape)==5:
        p1 = -F.max_pool3d(-img,(3,1,1),(1,1,1),(1,0,0))
        p2 = -F.max_pool3d(-img,(1,3,1),(1,1,1),(0,1,0))
        p3 = -F.max_pool3d(-img,(1,1,3),(1,1,1),(0,0,1))
        return torch.min(torch.min(p1, p2), p3)


def soft_dilate(img):
    if len(img.shape)==4:
        return F.max_pool2d(img, (3,3), (1,1), (1,1))
    elif len(img.shape)==5:
        return F.max_pool3d(img,(3,3,3),(1,1,1),(1,1,1))


def soft_open(img):
    return soft_dilate(soft_erode(img))


def soft_skel(img, iter_):
    img1  =  soft_open(img)
    skel  =  F.relu(img-img1)
    for j in range(iter_):
        img  =  soft_erode(img)
        img1  =  soft_open(img)
        delta  =  F.relu(img-img1)
        skel  =  skel +  F.relu(delta-skel*delta)
    return skel