DAY26：回溯算法（一）：回溯算法理论

课程链接：https://www.bilibili.com/video/BV1cy4y167mM/?spm_id_from=333.788

什么是回溯法

回溯法 - OI Wiki (oi-wiki.org)

回溯法是一种经常被用在 深度优先搜索（DFS） 和 广度优先搜索（BFS） 的技巧。

其本质是：走不通就回头。

回溯和递归是相辅相成的，只要有递归，就会有回溯。回溯通常都是在递归函数的下面，递归函数下面的部分就是回溯的逻辑。

二叉树在递归的过程中都会有回溯的操作，只不过有的题目用到了回溯，有的题目没有用回溯。

回溯法的效率

回溯法其实是一个纯暴力的搜索，并不是什么高效的算法。用这种算法的原因，是因为有些问题能暴力搜出来已经很好了。用for循环一层一层嵌套的话，根本搜不出来。依靠回溯法才能把结果搜出来。最多再剪枝一下。

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

回溯法用来解决哪些问题？

1.组合问题

组合问题一般是给你一个集合，例如给出{1，2，3，4}，要求在这个集合里找出大小为2的组合。这种组合包括{1，2}{1，3}{1，4}{2，3}{2，4}{3，4}。找出这些组合，就是一个组合问题。

也就是N个数里面按一定规则找出k个数的集合。

2.切割问题

切割问题通常是给一个字符串，问字符串有几种切割的方式。

或者再加限制条件，比如给你一个字符串，如何保证其子串都是回文子串？

也就是一个字符串按一定规则有几种切割方式

3.子集问题

我们继续用{1,2,3,4}来举例，1是子集，2是子集，1 3是子集，1 4也是子集……把它的子集全部列出来，就是子集问题。

这种问题用for循环嵌套其实是很困难的。

也就是一个N个数的集合里有多少符合条件的子集

3.排列问题

排列和组合的区别：组合是强调没有顺序的，但排列不是。

如果集合是{1,2}，只有一种组合，但是有两种排列，分别是{1,2}和{2,1}。排列强调元素的顺序，组合不强调元素顺序。

示例问题就是N个数按一定规则全排列，有几种排列方式

4.棋盘问题

包括N皇后，解数独，这些都是棋盘问题。这种问题用for也很难解决，必须用回溯搜索法。

如何理解回溯法？

回溯法是比较抽象的，如果想要更清晰的思路，可以将回溯法抽象成图形结构。只是脑内模拟会非常困难。

所有的回溯法都可以抽象为一个树形结构。所有回溯法都可以进行抽象。

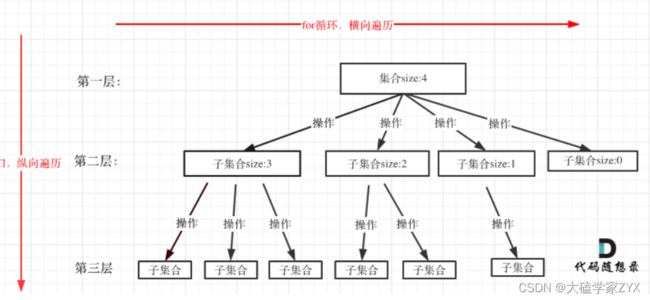
因为回溯就是一个递归的过程，递归一定是有终止的。回溯法通常可以抽象为一个N叉树，如下图所示。

树的宽度就是我们在回溯法中处理的集合大小，也就是每个节点所处理的集合大小。

在宽度上，我们通常是用for循环来进行遍历的。

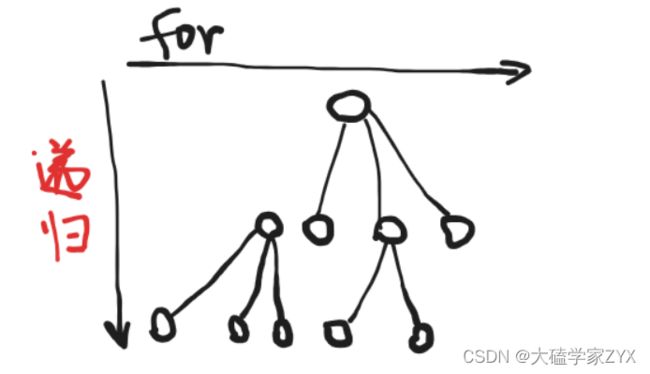
树的深度，就是递归的深度。因为递归一定是有终止的，纵方向上，就是递归来处理的。

回溯的所有问题，都可以抽象成这种树形结构。

更具体的版本：

注意图中，特意举例集合大小和孩子的数量是相等的！

回溯法的模板

一般来说，回溯法的递归函数都是没有返回值的，就是void。递归函数一般起名叫做backtracking.

参数上，回溯法的参数一般都是比较多的。不太容易一开始的时候就确定下来所有参数。

void backtracking(参数){
    //终止条件，递归一定有终止
    if(终止条件){
        //终止条件一般就是收集结果的时候，结果一般都在叶子节点
        //只有子集问题是在每一个节点都要收集
        收集结果;
        return;//不能忘记return
    }
    
    //单层搜索的逻辑，单层搜索一般是一个for循环，for遍历集合里的每一个元素
    //也可以对应这个节点所有的子节点个数
    for(选择：本层集合中元素（树中节点孩子的数量就是集合的大小）){
        //遍历每一个元素
        处理节点;例如把结果{1，2}放到一个数组里;
        //进入递归过程
         backtracking(路径，选择列表); 树形图里面一层一层往下走;
        //回溯
        回溯操作;撤销处理这个节点的情况;
        	例如找{1,2}之后，要把2弹出去重新变成1，再加入3
    }
    return;    
}

回溯法解决的问题都可以抽象为树形结构（N叉树）。