【零基础学机器学习 4】机器学习中的回归-线性回归

‍ 作者简介：程序员半夏 , 一名全栈程序员，擅长使用各种编程语言和框架，如JavaScript、React、Node.js、Java、Python、Django、MySQL等.专注于大前端与后端的硬核干货分享,同时是一个随缘更新的UP主. 你可以在各个平台找到我!
本文收录于专栏: 零基础学机器学习
专栏介绍:

本专栏将帮助您了解机器学习、其工作原理以及如何使用它。本教程包含以下内容:监督和无监督学习、线性回归、随机森林算法、朴素贝叶斯分类器、K-means聚类算法等基础学习基础知识，以及各种实战案例。

机器学习算法

机器学习算法分为三个领域：

• 监督学习
• 无监督学习
• 强化学习

这次我们只涉及监督学习，因为线性回归就属于这个领域。监督学习的两个最常见用途是：

• 回归
• 分类

回归分为三种类型：

• 简单线性回归
• 多元线性回归
• 多项式线性回归

线性回归的应用

经济预测

线性回归可用于确定国家或州在未来一个季度的经济增长。它也可以用于预测一个国家的国内生产总值（GDP）。

商品价格

线性回归可用于预测未来商品价格，无论价格是上涨还是下跌。

房屋销售

线性回归可用于估计建筑商在未来几个月内将销售的房屋数量和价格。

得分预测

基于以往的表现，线性回归可用于预测一个棒球运动员在即将到来的比赛中得分的数量。

在Python中理解线性回归

线性回归是一种统计模型，用于通过检查两个因素来预测自变量和因变量之间的关系：

1. 哪些变量特别是结果变量的重要预测因素？
2. 回归线在预测最高可能准确性方面有多重要？

为了理解“因变量”和“自变量”这两个术语，让我们以一个现实世界的例子来说明。

假设我们想根据降雨量来预测未来的农作物产量，使用的是有关过去农作物和降雨量的数据。

自变量

自变量的值不会因其他变量的影响而改变。自变量用于操作因变量。通常用“x”表示。在我们的例子中，降雨是自变量，因为我们无法控制雨水，但雨水控制着农作物 - 自变量控制着因变量。

因变量

当自变量的值发生任何变化时，该变量的值也会发生变化，如前所述。通常用“y”表示。在我们的例子中，农作物产量是因变量，它依赖于降雨量。

回归方程

具有一个自变量和一个因变量的最简单的线性回归方程是：

y = m * x + c

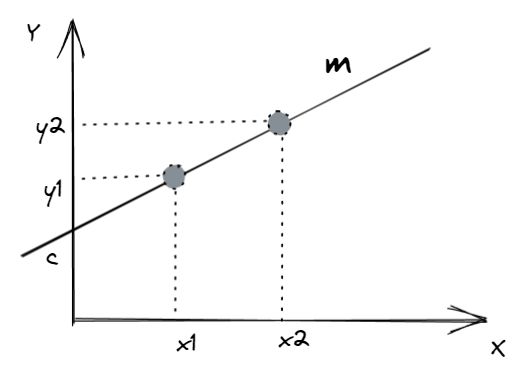
如下图所示：

我们绘制了两个点（x1，y1）和（x2，y2）。

让我们继续上面农作物产量的例子，并根据降雨量绘制农作物产量。在这里，降雨是自变量，农作物产量是因变量。

在这里，我们通过数据的中间绘制了一条直线，这条线是回归线。绿点表示的x是降雨量，在这个降雨量下的农作物产量预测就是红点代表的y值。

回归线背后的推理

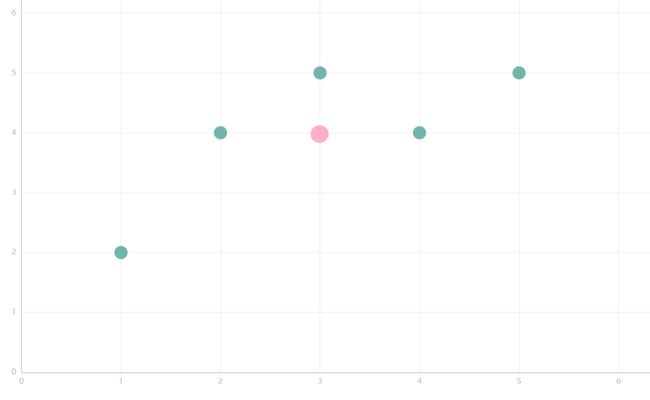
让我们考虑一个包含五行数据的样本数据集，并找出如何绘制回归线。我们将取两组数据，其中x是自变量，y是因变量：

x	y
1	2
2	4
3	5
4	4
5	5

接下来，我们计算x和y的平均值。x值的平均值为3，y值的平均值为4。

现在我们将讨论回归线方程。计算如下：

我们已经计算了x2、y2和x*y的值，以计算线的斜率和截距。计算出的值为：

m = 0.6

c = 2.2

线性方程为：

y = m*x + c

让我们使用线性方程找出相应x值的预测y值并绘制它们。

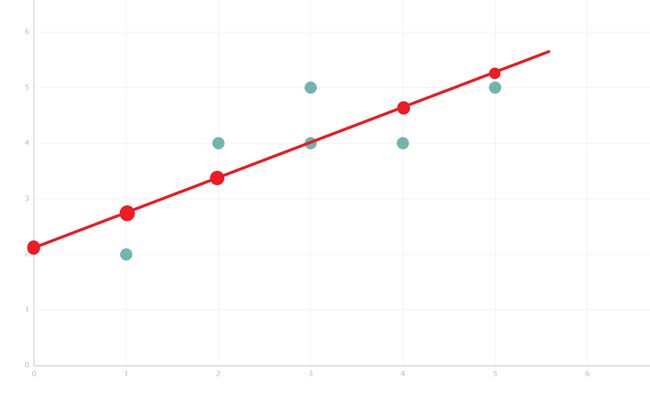在这里，绿色点表示实际的y值，红色点表示基于我们创建的模型的预测y值。实际值和预测值之间的距离称为残差或误差。最佳拟合线应该具有这些误差的最小平方和，也称为“e平方”。

您可以观察到，该回归线的平方误差和为2.4。我们检查每条线的误差，并确定具有最低e平方值的最佳拟合线。图形表示如下：

我们将线移动穿过数据点，以确保最佳拟合线在数据点和回归线之间具有最小的平方距离。

上述示例显示了最常用的最小化距离的公式。有许多方法可以最小化线和数据点之间的距离，例如使用平方误差的总和、绝对误差的总和和均方根误差。

到目前为止，我们只处理了两个值，即x和y。但在实际世界中，当你计算时只有两个值非常罕见。让我们谈谈当你有多个输入时会发生什么。

多元线性回归

在简单线性回归中，我们有以下方程式：

$$y=m\ast x+c$$
在多元线性回归中，我们有以下方程式：

$$y=m1x1+m2x2+m3x3+........+c$$
这里，我们有多个自变量x1、x2和x3，以及多个斜率m1、m2、m3等等。