机器学习之线性回归
机器学习之线性回归
一、线性回归简介
线性回归在数学上的表现可以是:y = wx + b、y = w1x1 + w2x2 + b、
y = w1x1 + w2x2 + w3x3+b…。总结来说,它是一种研究自变量和因变量的关系,是指一种预测性的建模技术。而自变量和因变量的关系简单来说就是要你求出上述公式里的参数w1、w2、w3、b等,所以我们线性回归算法的主要任务就是为了求出参数w1、w2、w3、b等。
二、线性回归的步骤
1.假设目标值(因变量y)与特征值(自变量x)之间线性关系(即满足一个多元一次方程,如:f(x)=w1x1+…+wnxn+b.)。
2.构建损失函数
3.通过损失函数的最小值,最后确定参数(最重要的一步)
三、损失函数
那么究竟什么是损失函数呢,其实就是我们所说的均方误差
我们在这里假设我目标值和特征值的线性关系为:y = wx + b。
有n组数据,目标值分别是(x):x1、x2、x3…xn。以及它们对应的特征值(y):y1、y2、y3…yn。根据我上述所说线性回归的主要任务是求出参数w、b,所以我们要怎么求出它呢???我们首先给w、b假设一个值,分别为2,1吧(随便假设)。所以我们就预测了一个模型y = 2x + 1,但这只是一个模型,它肯定是不准确的,我们用这个假设预测出的y值减去它真实的特征值(y1、y2…),它们之间就会有一个误差,我们将这每个数据的误差加起来,就可以得出一个总的误差,但这总的误差肯定也不准确,为什么这么说呢? 你看如果 (2 * x1 + 1)- y1 是一个负数,而(2 * x2 + 1)- y2是一个正数,那么它们相加起来误差反而会减小。所以我们为了避免出现这样的情况,我们就对每一组数据的误差求一个平方,这样加起来的就都是正数了,就可以反应出我们这个假设的模型对于真实数据的误差。我们管这种误差叫均方误差。用公式表示如下:
![]()
这个公式我们就是我要和大家说的损失函数(只是上述线性关系的损失函数啊,其它线性关系的损失函数以此类推)。那么我们知道损失函数或者说误差越小,我们的模型就越接近真实的特征值,那我们如何使它变小呢???
1.最小二乘法
我们还是以上面的线性关系:y = wx + b为例。我们得到了一个损失函数J(w,b),而它很明显是一个二次函数,我们现在要想让它的值变小,甚至是想求出它的最小值,按照我们常规求二次函数的最小值的方法,我们是不是该对它求导啊,而事实也是如此,我们分别对损失函数J(w,b)的两个参数w,b求偏导(注意,这里是对w,b求导,而不是对x求偏导),可以得到:
![]()
![]()
最后可以得到
![]()
![]()
但是这样上述计算量太大了,虽然可以交给机器去运算,但如果是大数据量的话我们可以考虑用以下方法
2.梯度下降法
首先你得先了解一下梯度的概念:梯度的本意是一个向量(矢量),表示某一函数(该函数一般是二元及以上的)在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
对于损失函数的图
如果我们一开始设的w值在最小值的右边,那我们尽量要往左边靠,就相当于要减去一个数,如果一开始设的w值在左边的话,那就要往右边靠,那有没有一个算式可以解决这个问题呢???
![]()
我们可以看到这个公式(先不看\alpha,先把它看作任何正数),当我设的值是w2的时候,那么它的偏导是不是个正数啊,那么我w2减去一个正数是不是就往最小值靠近了啊,同样,当我设的值是w1的时候,那么它的偏导不就是个负数吗,我w1减去一个负数,不就是加了一个正数吗,那我就向最小值靠近了一步。
公式里的alpha指的是学习率。它的作用是为了控制你往最小值靠近的“步子”的大小,如果它很大的话,那你的“步子”就大了啊,有可能就会“跨过”最小值,太小的话,又会需要“跨”很多的“步子”,所以它的设置得根据你的需要来。
![]()
面对有多个参数(w1,w2,w3…wn,b)以此类推,推出损失函数最小的时候,它们对应的值就可以了。
import matplotlib.pyplot as plt
x = [14.1,15.1,16.1,15.3,14.2,14.5,14.6,14.8,16.3,16.6,15.6,16.7,14.7,16.2,16.7,14.8,14.9,15.9,16.3,17.0,15.0,16.3,17.1,16.0,17.2,17.4,15.5,16.8,17.4,16.9]
y = [15.8,16.3,14.5,16.6,16.7,15.0,14.9,15.2,15.3,16.6,17.0,16.4,16.5,15.4,15.8,14.8,16.0,17.3,15.7,14.4,15.8,16.7,14.9,16.9,15.5,16.6,17.7,18.0,15.9,18.0]
#这里是我随便创造的数据,一共30个
#这里我将数据分为了训练集和测试集
x_train = x[0:20]
y_train = y[0:20]
x_test = x[20:]
y_test = y[20:]
#给参数w和b的初始值分别为1.0和-1.0,以及学习率为0.0001,求10000次参数
w_start = 1.0
b_start = -1.0
learn = 0.0001
times = 10000
for i in range(times):
sum_w = 0
sum_b = 0
#这里就是我们的梯度下降法,通过它,使我们的损失函数变小,求出我们要的新参数w和b
for i in range(len(x_train)):
sum_w += (y_train[i] - w_start * x_train[i]-b_start) * (-x_train[i]) #就是对w的偏导数
sum_b += (y_train[i] - w_start * x_train[i]-b_start) * (-1) #对b的偏导数
w_start = w_start - 2 * sum_w * learn #更新这么多次,如果偏导能到0的话,他就不会更新了
b_start = b_start - 2 * sum_b * learn
plt.figure(figsize=(20,8))#改变图片大小
plt.scatter(x_train, y_train)#画出我们训练集的散点图
plt.plot([i for i in range(0,20)],[(w_start * i + b_start) for i in range(0,20)])#画出我们通过梯度下降法求出来的新的参数w,b的y = wx + b的直线图
plt.show()
#下面这里是为了检测我得出的线性回归模型理想程度
#这是训练集的所有真实数据与我模型(y=wx+b)相减得出来的误差值
total_train_loss = 0
for i in range(len(x_train)):
y_hat = w_start * x_train[i] + b_start
total_train_loss += (y_train[i] - y_hat) ** 2
print(total_train_loss)
#这是测试集的所有真实数据与我模型(y=wx+b)相减得出来的误差值
total_test_loss = 0
for i in range(len(x_test)):
y_hat = w_start * x_test[i] + b_start
total_test_loss += (y_test[i] - y_hat) ** 2
print(total_test_loss)
#这样一看,感觉这个模型很不理想啊.......但没关系,这个代码主要是为了让大家更好的了解线性回归
3.正规方程
正规方程一般用在多元线性回归中,原因等你看完也就能理解为什么。所以这里不再用一元线性回归举栗子了。
同样,假设有n组数据,其中目标值(因变量)与特征值(自变量)之间的关系为:
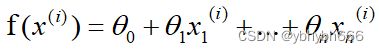
其中i表示第i组数据,这里先直接给出正规方程的公式:
![]()
推导过程如下:
记矩阵
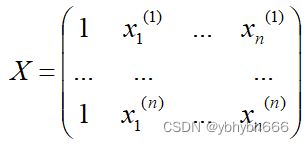
向量
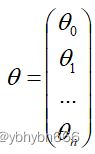

则![]()
损失函数为:
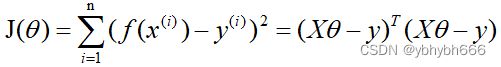
对损失函数求导并令其为0,有

解得
![]()
到此,就求出了所有系数θ。不过正规方程需要注意的是XTX,在实际中可能会出现是奇异矩阵,往往是因为特征值之间不独立。这时候需要对特征值进行筛选,剔除那些存在线性关系的特征值(好比在预测房价中,特征值1代表以英尺为尺寸计算房子,特征值2代表以平方米为尺寸计算房子,这时特征值1和特征值2只需要留1个即可)。
- 梯度下降法是通用的,包括更为复杂的逻辑回归算法中也可以使用,但是对于较小的数据量来说它的速度并没有优势
- 正规方程的速度往往更快,但是当数量级达到一定的时候,还是梯度下降法更快,因为 正规方程中需要对矩阵求逆,而求逆的时间复杂的是n的3次方
- 最小二乘法一般比较少用,虽然它的思想比较简单,在计算过程中需要对损失函数求导并令其为0,从而解出系数θ。但是对于计算机来说很难实现,所以一般不使用最小二乘法。