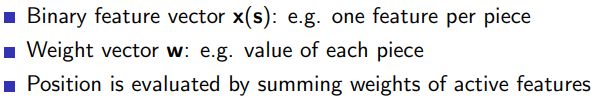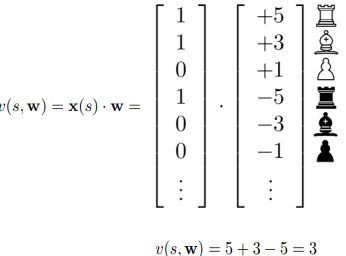David Silver Lecture 10: Classic Games
1 state of the art
1.1 Outline
1.1.1 Why Study Classic Games
1.1.2 AI In Games: state of the Art
2 Game Theory
2.1 Outline
2.1.1 Optimality in Games
2.1.2 Single-Agent and Self-Play Reinforcement Learning
2.1.3 Two-Player Zero-Sum Games
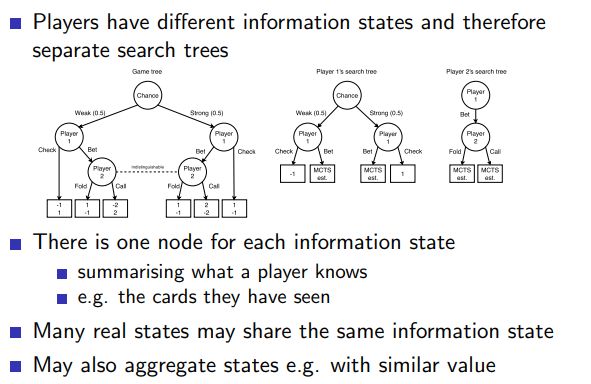
2.1.4 Perfect and Imperfect Information Games
3 Minimax Search
3.1 outline
3.1.1 Minimax
Minimax搜索是在决策理论和游戏理论中用于决定最优策略的一种方法,特别适用于对抗性的环境(例如,国际象棋或者井字游戏)。基本思想是最大化我们的最小可能回报:最大化在对手做出最佳对我们不利决策的情况下我们可以获得的收益。
Minimax搜索的核心是深度优先遍历的方式去查看所有可能的游戏结果,然后从这些结果中回溯,对每个节点做一个决策:如果节点是我们的回合,我们会选择最大的值(因为我们希望最大化我们的收益);如果节点是对手的回合,我们会选择最小的值(因为我们假设对手会尝试最大化他们的收益,从而最小化我们的收益)。
让我们来看一个简单的例子,下面是一个在井字游戏(tic-tac-toe)中使用Minimax搜索的Python代码。
在这个代码中,minimax 函数接收一个游戏板,一个深度值(用于跟踪我们正在查看的是哪个回合),和一个布尔值,用于决定我们是应该最大化(如果是我们的回合)还是最小化(如果是对手的回合)得分。这个函数首先检查游戏是否已经结束(如果我们或者对手已经赢了,或者没有剩余的空格)。如果游戏已经结束,它就返回当前得分(1表示我们赢了,-1表示我们输了,0表示平局)。如果游戏没有结束,它就遍历所有的空格,对于每一个空格,试图放置一个我们的棋子或者对手的棋子(取决于当前是谁的回合),然后递归地调用minimax 函数。在所有可能的移动中,我们选择最大的得分(如果是我们
def minimax(board, depth, is_maximizing):
score = evaluate(board)
if score == 1:
return score
if score == -1:
return score
if is_moves_left(board) == False:
return 0
if is_maximizing:
best = -1000
for i in range(3):
for j in range(3):
if board[i][j] == '_':
board[i][j] = 'x'
best = max(best, minimax(board, depth + 1, not is_maximizing))
board[i][j] = '_'
return best
else:
best = 1000
for i in range(3):
for j in range(3):
if board[i][j] == '_':
board[i][j] = 'o'
best = min(best, minimax(board, depth + 1, not is_maximizing))
board[i][j] = '_'
return best
3.1.2 Value Function in Minimax Search
3.1.3 Binary-Linear Value Function
在Minimax策略中,有一种方法可以减少搜索树的复杂度,这就是使用启发式评估函数(也被称为价值函数)。这个函数为每一个局面提供了一个估计的分值,这样我们就可以仅仅搜索到一定的深度,而不是一直搜索到游戏的终局。对于这种评估函数,我们的目标是对真实的游戏价值做出最好的猜测。
在井字游戏中,我们可以使用一个简单的评估函数,比如“行、列或对角线上我方棋子的数量减去对手棋子的数量”。这个函数值大于0表示我们正在赢,小于0表示我们正在输,等于0表示平局。
下面是使用这个评估函数的Minimax搜索的Python代码:
def evaluate(board):
# Check rows, columns and diagonals for winner
# Return 1 if we are winning, -1 if we are losing, 0 otherwise
# ...
def minimax(board, depth, is_maximizing, alpha, beta):
score = evaluate(board)
if abs(score) == 1:
return score
if is_moves_left(board) == False:
return 0
if is_maximizing:
best = -1000
for i in range(3):
for j in range(3):
if board[i][j] == '_':
board[i][j] = 'x'
best = max(best, minimax(board, depth + 1, not is_maximizing, alpha, beta))
board[i][j] = '_'
alpha = max(alpha, best)
if beta <= alpha:
break
return best
else:
best = 1000
for i in range(3):
for j in range(3):
if board[i][j] == '_':
board[i][j] = 'o'
best = min(best, minimax(board, depth + 1, not is_maximizing, alpha, beta))
board[i][j] = '_'
beta = min(beta, best)
if beta <= alpha:
break
return best
在这个代码中,evaluate函数提供了一个启发式的评估,这样我们就不必总是搜索到游戏的终局。此外,我们还引入了alpha-beta剪枝,这是一种可以显著减少搜索树大小的技术。在每一步,我们都跟踪两个值:alpha是到目前为止找到的最佳的(即,最高的)值,这个值是我们知道我们至少可以达到的;beta是到目前为止找到的最坏的(即,最低的)值,这个值是我们知道对手至多可以将我们限制到的。如果我们发现某一步的alpha大于或等于beta,那么我们就可以停止在这一步下面的搜索,因为我们已经知道这一步肯定不会被选择。
在这个代码中,Alpha-Beta剪枝主要体现在这些部分:
1.alpha = max(alpha, best):我们在Maximizer的每次迭代中更新alpha值。alpha在这里代表了在所有已经探索过的Maximizer节点中,得到的最好的(最大的)评估值。即,这是Maximizer目前至少能够达到的最大值。
2.beta = min(beta, best):我们在Minimizer的每次迭代中更新beta值。beta在这里代表了在所有已经探索过的Minimizer节点中,得到的最坏的(最小的)评估值。即,这是Minimizer目前至多能够使Maximizer降低到的最小值。
3.if beta <= alpha: break:如果在某一点,beta值(即,Minimizer所能达到的最小值)已经小于或等于alpha值(即,Maximizer所能达到的最大值),那么就不再继续在这个节点下面进行搜索,因为我们知道这个分支不可能会被实际采用(在完全理性的对手假设下)。这一步是Alpha-Beta剪枝的主要部分,通过它,我们能够避免探索那些确定不会影响结果的节点,从而显著减少搜索的复杂度。
Alpha-Beta剪枝基于的主要思想是:如果一个节点已经确保了当前玩家的得分不可能超过之前某个节点的值,那么就没有必要再探索这个节点以下的分支,我们可以“剪枝”,即忽略这部分的搜索。这种方式可以极大地提高Minimax搜索的效率,特别是在搜索树比较大的时候。
在Minimax算法中,score和best两个变量是用来评估和记录当前的游戏状态的。
首先,score的目的是评估当前的棋盘状态。这是通过调用evaluate(board)函数完成的。evaluate(board)函数返回的是一个评估值,这个值可以帮助我们了解当前局面对我们是否有利。例如,如果evaluate(board)返回的值为1,那么这表示我们正在赢得比赛,如果返回的值为-1,表示我们正在输,如果返回的值为0,表示比赛当前处于平手的状态。
然后,best的目的是记录我们在检查所有可能的下一步棋后,可以获得的最佳评估值。例如,如果我们正在进行最大化操作(也就是我们正在找可以让我们获得最大评估值的下一步棋),我们就把best初始化为一个非常小的数(例如-1000),然后对每一个可能的下一步棋,我们都把这一步棋的评估值和当前的best进行比较。如果这一步棋的评估值更大,我们就更新best为这一步棋的评估值。在我们检查完所有可能的下一步棋后,best就会是所有可能下一步棋中的最大评估值。反之,如果我们正在进行最小化操作(也就是我们正在找可以让对手获得最小评估值的下一步棋),我们就把best初始化为一个非常大的数(例如1000),然后按照类似的方式更新best。
因此,score是用来评估当前的棋盘状态,而best是用来记录在当前的棋盘状态下,我们可以获得的最佳评估值。
3.1.4 Deep blue
3.1.5 Chinook
4 Self-play Reinforcement Learning
4.1 Outline
4.1.1 Self-play Temporal-Difference Learning
4.1.2 Policy Improvement with Afterstates
4.1.3 Self-play TD in othello: logistello
4.1.4 Reinforcement Learning in Logistello
4.2 TD-Gammon
4.2.1 TD Gammon: non-linear Value function approximation
4.2.2 Self-play TD in Backgammon: TD-Gammon
4.2.3 TD Gammon: Results
5 Combining Reinforcement Learning and Minimax Search
5.1 outline
5.1.1 simple TD
simple TD其实就是TD( λ \lambda λ)
import numpy as np
# This is a simple gridworld environment
# The agent starts at (0, 0) and the goal is to reach (4, 4)
# At each time step, the agent can move up, down, left or right
# The episode ends when the agent reaches the goal
# The reward is -1 at each time step
class Gridworld:
def __init__(self):
self.x = 0
self.y = 0
def step(self, action):
if action == 0: # up
self.y = max(self.y - 1, 0)
elif action == 1: # down
self.y = min(self.y + 1, 4)
elif action == 2: # left
self.x = max(self.x - 1, 0)
elif action == 3: # right
self.x = min(self.x + 1, 4)
reward = -1
done = (self.x == 4) and (self.y == 4)
return (self.x, self.y), reward, done
def reset(self):
self.x = 0
self.y = 0
return (self.x, self.y)
# Let's use TD(0) to learn the value function
env = Gridworld()
value_function = np.zeros((5, 5))
alpha = 0.1 # learning rate
discount = 1.0 # discount factor
for episode in range(10000):
state = env.reset()
while True:
action = np.random.choice([0, 1, 2, 3]) # choose action randomly
next_state, reward, done = env.step(action)
value_function[state] = value_function[state] + alpha * (reward + discount * value_function[next_state] - value_function[state])
state = next_state
if done:
break
print(value_function)
5.1.2 Simple TD: Result
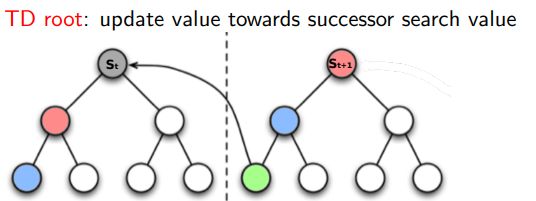
5.1.3 TD root
在强化学习中,TD Root 是一种重要的临时差分学习 (Temporal Difference Learning) 方法,被用来估算出最优的策略。
TD Root 主要是用在棋类等回合制游戏的AI设计中,它可以帮助程序实现在没有明确的游戏结果反馈时预测走棋的结果。算法主要基于Monte-Carlo Tree Search (MCTS) 但在结果反馈时采用 TD(λ) 方法。
TD(λ) 是 TD(0) 的泛化,其中 λ 是一个在 0 到 1 之间的参数,这个参数控制回报的计算方式。在 TD(0) 中,我们仅使用下一个状态的估计值来更新当前的状态估计值,即 λ = 0。在 Monte Carlo 方法中,我们使用从当前状态开始的所有未来奖励的真实值来更新当前的状态估计值,即 λ = 1。在 TD(λ) 中,我们使用下一个状态的估计值和所有未来奖励的真实值的一个加权和来更新当前的状态估计值,这个加权和由 λ 来控制。
具体实现 TD Root 的 Python 代码较为复杂,需要结合 MCTS 和 TD(λ) 两个算法的实现。一个可以参考的是DeepMind的 AlphaGo 和 AlphaZero 的论文,这些论文中就使用了类似的方法。
要注意的是,到目前为止(截至2021年),TD Root 在实践中的应用还不是很广泛,主要被用于棋类等回合制游戏的AI设计,其在其他类型的问题上的应用还需要进一步的研究。
5.1.4 TD Root in Checkers: Samuel’s Player
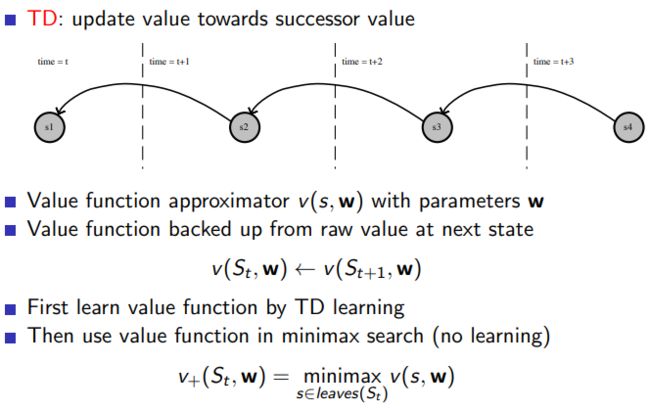
5.1.5 TD Leaf
在强化学习中,TD Leaf 是一种基于 Temporal Difference Learning 的方法,被广泛应用于棋类等回合制游戏的 AI 设计中。TD Leaf 主要用于在没有明确的游戏结果反馈时预测走棋的结果。
在传统的 Minimax 搜索树中,所有的节点都有一个评分,而在实际的比赛中,只有最后的结果是确定的,中间的过程是充满了不确定性的。为了解决这个问题,TD Leaf 提出了一种方法,即只对叶子节点(leaf node)的评分进行更新,并将叶子节点的评分反馈给其祖先节点。
具体的操作方法是,先随机选择一条从根节点到叶子节点的路径,然后对叶子节点进行一次模拟走棋,模拟走棋的结果将作为这个叶子节点的评分。然后,我们用这个叶子节点的评分来更新所有祖先节点的评分,更新的方式是,如果叶子节点的评分比祖先节点的评分高(或者低),那么就把祖先节点的评分提高(或者降低)一点。
TD Leaf 的 Python 代码实现通常较为复杂,需要具备 Minimax 搜索、TD 学习等多个方面的知识。并且,TD Leaf 的效果也会受到环境复杂度、评分函数的设计、模拟走棋的策略等多个因素的影响。因此,这里无法给出一个简单的 Python 代码示例。如果你对 TD Leaf 感兴趣,我建议你阅读一些深入的教程或者相关的学术论文,来获取更多的信息。