加法器种类介绍

二进制加法器

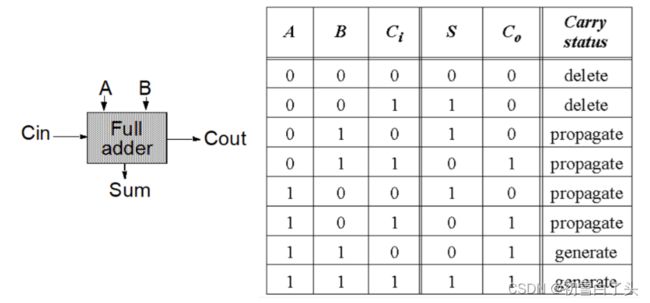
二进制加法器接收加数A和B,以及进位Ci,输出和S,以及进位输出Co.二进制加法器的真值表如下：

逻辑表达式：

$S=A\oplus B\oplus C_i$

$C_o=AB+B{C}_i+A{C}_i$

从实现的角度，可以将S和Co定义为一些中间信号：

• $G=AB$：进位产生（generate）为1时，保证 $C_o=1$
• $D=\bar{A}\cdot \bar{B}$：进位取消（delet）为1时，保证 $C_o=0$
• $P=A\oplus B$：进位传播（propagate）为1时，保证 $C_o=C_i$

上面的几个变量均和 $C_i$无关，可以将逻辑表达式写为这些值的函数：

$C_o(G,P)=G+P{C}_i$

$S(G,P)=P\oplus C_i$

二进制全加器的一个特性是，输入反向的话，输出也反向，可以通过逻辑表达式观察得到：

逐位进位加法器

也叫行波进位加法器。通过把N个二进制全加器（FA)串联起来得到。

对于某些输入信号，不会发生行波进位传递，而对于另一些信号，进位需要从最低有效位波动到最高位，这样一条路径称为 关键路径（critical path),关键路径的延时定义为最坏情况下的延时。在最坏情况下的延时可以写为：

$$t_{adder}=(N-1)t_{carry}+t_{sum}$$

其中，$t_{carry}$为 $C_i$到$C_o$的延时，$t_{sum}$是$C_i$到$S$的延时。

静态CMOS加法器

如果直接用CMOS实现上面的二进制全加器，将会消耗36个管子，而实际上可以通过将逻辑表达式变形，来使得“和”与“进位产生”电路共享某些逻辑：

$$C_o=AB+B{C}_i+A{C}_i$$

$$S=AB{C}_i+\overline{C_o}(A+B+C_i)$$

从真值表很容易验证这与之前的式子等价。并且只需要28管：

上面电路用到了一个小技巧，就是将$C_i$关键信号放在靠近输出端，可以避免内部节点充放电等待$C_i$信号的到来，改善输出的延时。

缺陷：

• 进位产生与和产生电路中堆叠了很多PMOS管
• $C_o$信号的本征负载电容很大，包括两个扩散电容，6个栅极电容加上布线电容。
• 在进位产生电路中经过了两个反向级，如果进位链输出的负载很小，两级逻辑引起额外的延时。
• 和的产生要求一个额外的逻辑级

延时优化：利用全加器的反向特性，输入反向输出也反向，可以在加法器链中引入输入反向的全加器：

图中的所有全加器的进位输出都不需要加反相器，这样大大减少了进位链的延时。

镜像加法器（mirror adder)

镜像加法器的特点：

• 基于G,D,P变量
• 取消了进位反向门
• PDN和PUN不再是对偶的CMOS结构，而是对称结构。
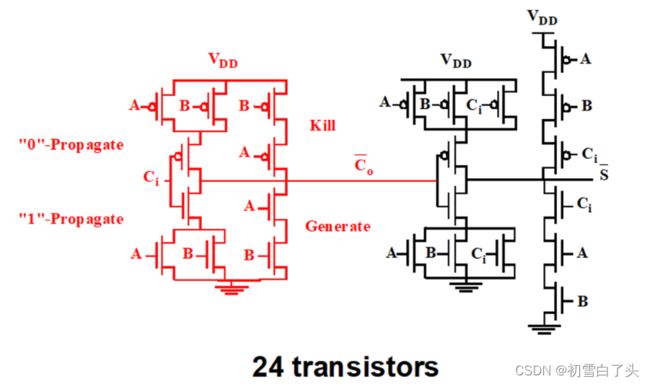
• 只消耗24个晶体管
• 只有在进位产生电路的管子需要优化尺寸改善速度，求和电路的晶体管都可以使用最小尺寸。关键点在于使 $C_o$处电容最小。

$$\begin{gathered} G=AB， \\ D=\bar{A}\cdot \bar{B}， \\ P=A\oplus B（与A+B等价） \\ {C}_o(G,P)=G+P{C}_i， \\ S=AB{C}_i+\overline{C_o}(A+B+C_i) \end{gathered}$$

可以分析一下镜像加法器的工作方式，实际上镜像加法器的进位电路巧妙利用了进位产生，消除和传播：

• 当A=B=1时，G=1,表示进位产生，此时通过PDN的两个串联NMOS可以将输出拉低，得到Co的反向信号，并且此时PUN不导通；

• 当A=B=0时，D=1,表示进位消除，此时通过PUN的两个串联PMOS可以将输出拉高，得到Co的反向信号；并且此时PDN不导通；

• 当A和B不全为1时，P=1,表示进位传播。PUN和PDN都部分导通(输入为A和B的PMOS和NMOS都有一个导通)，上拉还是下拉取决于进位输入$C_i$，与公式中的$P{C}_i$相匹配，并且输出 $C_o$的反向信号。

• 对于和电路也可以同样分析。

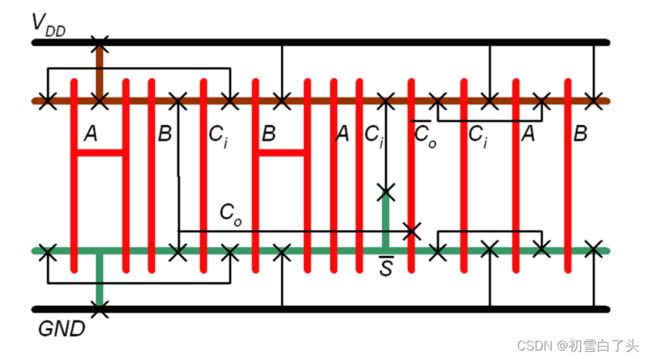
镜像加法器的版图：

传输门型加法器

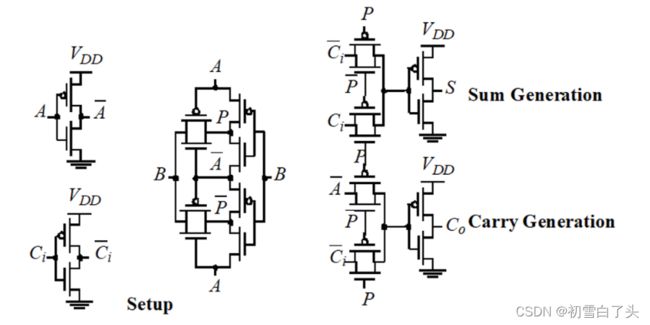
使用传输门来构建和与进位电路，特点是它的和与进位输出具有近似的延时。也是24管。

$$\begin{gathered} G=AB， \\ D=\bar{A}\cdot \bar{B}， \\ P=A\oplus B（与A+B等价） \\ {C}_o(G,P)=G+P{C}_i， \\ S(G,P)=P\oplus C_i \end{gathered}$$

需要注意的是，在Co的产生电路中，用到了一个变换：

$$Co=\overline{\bar{P}\cdot \bar{A}+P\cdot \overline{C_i}}=P{C}_i+A{C}_i+A\bar{P}=P{C}_i+A\cdot A\odot B=P{C}_i+AB$$

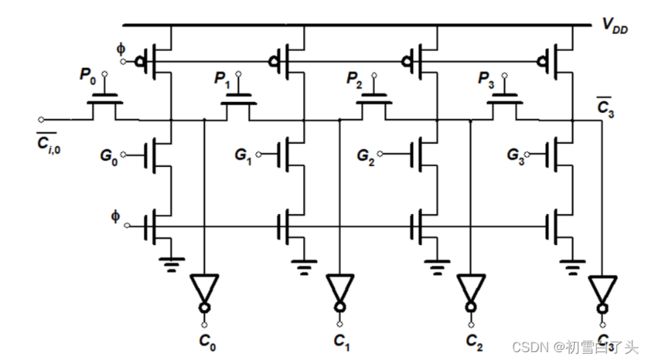
曼彻斯特进位链加法器

在传输门加法器中，进位电路可以进行优化，比如可以使用进位消除和产生信号来控制进位电路（下左图）：

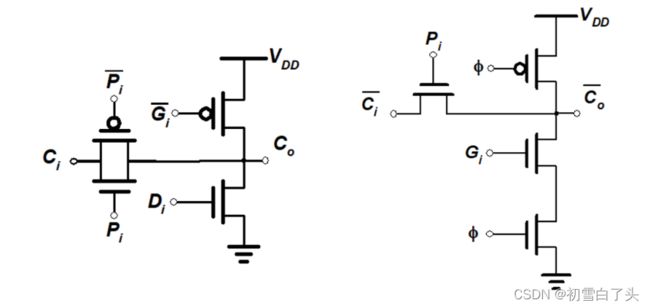
此外，使用动态逻辑可以更加简化，传输门也只需要使用单管，并且不需要进位取消电路。如上面右图。在预充电（ϕ=0)时，输出节点充到VDD，表示Co=0;求值时，根据G和Ci信号决定有无进位产生。下图是曼彻斯特进位链的构造：

上图中加法器进位链在最坏情况下的延时模型可模拟为线性RC网络。其延时为：

$$t_p=0.69\sum _{i=1}^N{C}_i(\sum _{j=1}^i{R}_j)=0.69\frac{N(N+1)}{2}RC$$

版图：

进位旁路加法器(Carry-Bypass Adder)

旁路进位加法器又叫进位跳跃加法器（carry-skip adder) ：

基本思路是增加一条进位旁路，通过进位选择信号$BP=P_0{P}_1\dots P_n$信号来选择进位输出是否直接选择最底层的进位进行输出。进而加快加法器。

曼彻斯特进位链实现的旁路加法器：

从上图中可以发现，当BP为高时，直接输出进位输入，而BP不为高时，则输出由中间的某些G信号决定，与Ci无关。这一性质可以极大加速加法器链，因为若干个这样的模块串联在一起时，实际上各个模块的进位电路中直到选择器之前的部分都可以并行地执行，而无需等待上级进位信号。

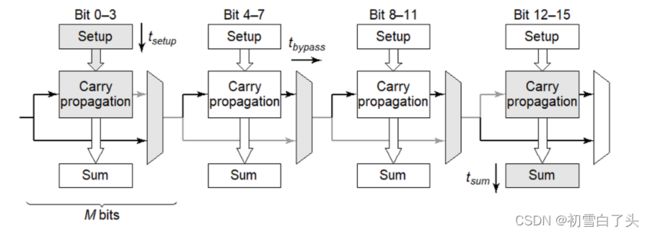
下面来计算旁路加法器的传播延时。首先对于N级的旁路进位加法器，假设其被划分为（N/M）个等长的旁路，每个旁路含有M位：

上图中灰色部分为关键路径。其延时可以表示为：

$$t_p=t_{setup}+M{t}_{carry}+(\frac{N}{M}-1)t_{bypass}+(M-1)t_{carry}+t_{sum}$$

可以看到，虽然旁路加法器的延时仍然关于N呈线性关系，但斜率除以了一个M，但是多了几个常数项，所以反映到下图的延时和级数N的关系曲线中就会发现，当N比较大时旁路加法器优于逐位进位，但N比较小（4-8）时，反而比逐位进位差。

线性进位选择加法器（Linera Cary-Select Adder)

线性进位选择加法器其实跟上面的旁路加法器类似，但是旁路加法器可以工作的一个条件是进位链中要使用G信号或者D信号来保证不选择旁路时加法器链的输出也跟输入进位Ci无关。因此旁路加法器需要额外的BP信号（每级P相与）配合进位产生信号G来控制进位链。另外一种方法是使用线性进位选择加法器，其工作更加简单粗暴，为了使得加法器链的进位输出跟输入解耦，直接考虑进位输入的两种可能值，提前计算两种可能结果，等到输入进位到来直接根据进位值选择哪条路径输出即可，这意味着同时实现了0和1进位输入的两个进位路径：

付出的代价是一个额外的进位路径和一个多路开关，大概等于逐位进位结构的30%。可以推导进位选择加法器的传播延时为：

$$t_p=t_{setup}+M{t}_{carry}+(\frac{N}{M})t_{mux}+t_{sum}$$

可见其传播延时仍然关于N呈线性关系。

平方根进位选择加法器（Square-Root Carry-Select Adder)

在上面的线性选择加法器中，每级分配相同的全加器，因此每级的延时都相同，每级进位链的结果在上一级的多路开关信号到来前已经稳定下来，可见在后面的几级在时刻5已经完成，但每级等待的时间越来越长，如图：

如果能够使后级不需要等待前一级多路开关的信号，而是在刚求完本级就正好接受到前级信号，就能消除这个等待时间：

上图就是平方根进位选择加法器，其与线性选择加法器的区别只在于每级的位数逐级递增。通过这种方式，每级在计算完本级的进位结果的同时上一级的多路开关信号正好到来。假设总共含有P级，第一级为M位。则有

$$N=M+(M+1)+(M+2)+\cdots +(M+P-1)=\frac{p^2}{2}+P(M-\frac{1}{2})$$

如果M<$N=\frac{P^2}{2}$,$P=\sqrt{2N}$因此其传播延时可写为：

$$t_p=t_{setup}+M{t}_{carry}+(\sqrt{2N})t_{mux}+t_{sum}$$

从公式可以看到，由于此处的M是初级的位数，一般都比线性选择加法器的小，延时并且跟根号2N呈线性关系，所以反应到延时和级数曲线中，平方根进位选择加法器跟纵轴交点要小于线性选择，且当N比较大时斜率远小于线性选择加法器：

超前进位加法器（Carry-lookahead Adder)

a. 单一超前进位加法器

上面的选择和旁路加法器虽然能减少延时，但逐级进位效应仍然存在。超前进位加法器解决了这一问题。其基本思想是：N位加法器的每一位上都有下面的关系：

$$C_{o,k}=f(A_k,B_k,C_{o,k-1})=G_k+P_k{C}_{o,k-1}$$

通过展开$C_{o,k-1}$，一直展开到第一级可以彻底消除每级进位的前一级的依赖，代价是实现加法器的逻辑逐级增加：

下面是一个四级超前进位加法的实现，利用了对偶性（类似镜像加法器）：

局限：单一超前进位加法器只在N比较小（<5)时使用，实际上的延时还是随位数线性增加的，这主要由下面的因素决定：

• 大的扇入使得在N较大时极慢
• 如果用较为简单的门实现，则需要多个逻辑层次，也会增加延时
• 某些信号的扇出常常过度增加，使得加法器更慢,例如G0和P0信号出现在后面的每级中，导致线电容较大

b. 对数超前进位加法器

将进位传播和进位产生组织成递归的树状结构：

在上面的公式中，进位传播被分解成两位的子组合$G_{i:j},P_{i:j}$称之为块进位产生和块进位传播信号。引入一个新的布尔运算，称之为点操作(⋅)：

$$(G,P)\cdot (G^{\prime },P^{\prime })=(G+P{G}^{\prime },P{P}^{\prime })$$

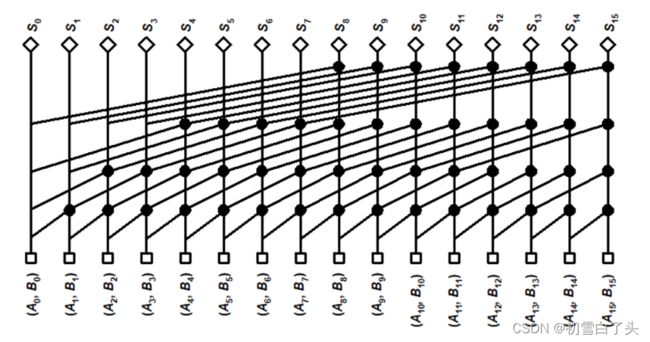
利用这个操作可以分解$(G_{i:j},P_{i:j})=(G_{i:k},P_{i:k})\cdot (G_{k-1:j},P_{k-1:j})$,点操作服从结合律，不服从交换律。利用点操作的结合律，可以构成一个树结构来计算所有2i−1个位置上的进位，并且只需要 $lo{g}_2(N)$就可计算出来。因此对数加法器可以将传播延时降低到 $lo{g}_2(N)$。下面是基于点操作的基2 kogge-Stone草签仅为对数加法器原理图。其中白色小方格表示建立P和G信号，黑点表示点操作，菱形表示和产生。

对于N=16的情形，整个加法器需要49个逻辑门。

动态逻辑实现加法器

下面是用动态多米诺逻辑实现的加法器进位产生和传播信号电路。

以及多米诺逻辑实现的点操作电路：

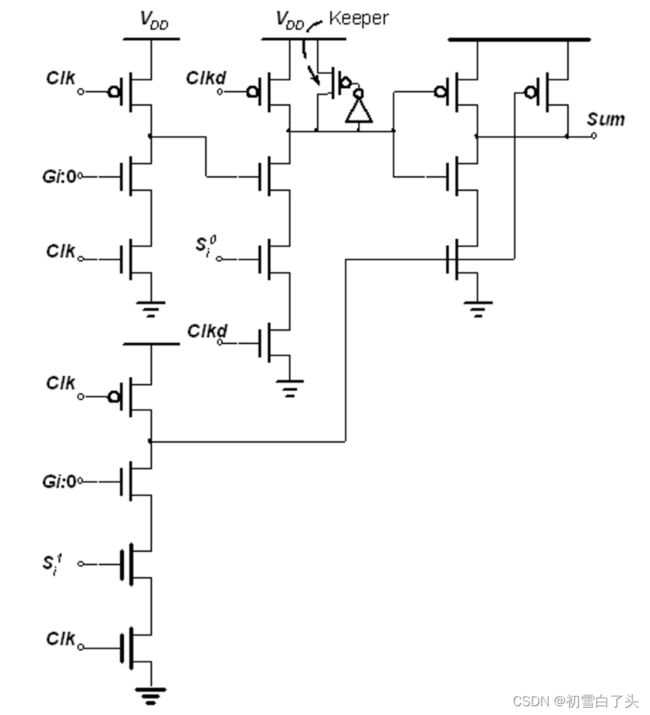
还需要配套的求和电路：

其中$S_i^0=\overline{a_i\oplus b_i},S_i^1=a_i\oplus b_i$.上图中的保持器是重要的，因为前面两级多米诺逻辑违反了多米诺的设计规则：两个动态门串联在一起而没有在中间插入反相器。如果用同一个时钟求值，则会第二个门的输出可能会有毛刺。

总结

各类加法器传播延时和面积与级数的关系图：