DS数据结构--求到各顶点的最短路径（迪杰斯特拉算法）

目录

1.引言

求最小路径这个算法我觉得是难度比较大的了，主要是它的思路比较抽象复杂，不好理解

其实它的思路和prim算法比较接近，要是有学过prim算法的话会更好地理解迪杰斯特拉算法。

2.接下来讲一下大概思路吧，源码在最下面

​

3.非递归算法如下，思路源自于大话数据结构

---

1.引言

求最小路径这个算法我觉得是难度比较大的了，主要是它的思路比较抽象复杂，不好理解

其实它的思路和prim算法比较接近，要是有学过prim算法的话会更好地理解迪杰斯特拉算法。

先上题目要求

题目描述
给出一个图的邻接矩阵，输入顶点v，用迪杰斯特拉算法求顶点v到其它顶点的最短路径。

输入
第一行输入t，表示有t个测试实例

第二行输入顶点数n和n个顶点信息

第三行起，每行输入邻接矩阵的一行，以此类推输入n行

第i个结点与其它结点如果相连则为距离，无连接则为0，数据之间用空格

隔开。第四行输入v0，表示求v0到其他顶点的最短路径距离

以此类推输入下一个示例

输出
对每组测试数据，输出：

每行输出v0到某个顶点的最短距离和最短路径

每行格式：v0编号-其他顶点编号-最短路径值----[最短路径]。没有路径输出：v0编号-其他顶点编号–1。具体请参考示范数据

样例输入
2
5 0 1 2 3 4
0 5 0 7 15
0 0 5 0 0
0 0 0 0 1
0 0 2 0 0
0 0 0 0 0
0
6 V0 V1 V2 V3 V4 V5
0 0 10 0 30 100
0 0 5 0 0 0
0 0 0 50 0 0
0 0 0 0 0 10
0 0 0 20 0 60
0 0 0 0 0 0
V0
样例输出
0-1-5----[0 1 ]
0-2-9----[0 3 2 ]
0-3-7----[0 3 ]
0-4-10----[0 3 2 4 ]
V0-V1–1
V0-V2-10----[V0 V2 ]
V0-V3-50----[V0 V4 V3 ]
V0-V4-30----[V0 V4 ]
V0-V5-60----[V0 V4 V3 V5 ]
————————————————
版权声明：本文为CSDN博主「晴夏。」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_43757333/article/details/110389973

2.接下来讲一下大概思路吧，源码在最下面

1.setmatrix函数就是用来接收矩阵的，在ShortestPath()函数中，最后面的几行也是输出，

  前面的几行是初始化，当然了要先理解前面初始化的那些数值的意义都是什么

初始化各类数据部分

 

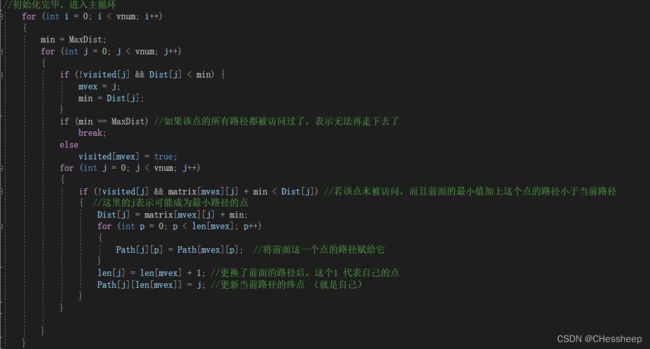
因此主要的算法我们只需要关注中间那二十行代码就可以了

 总共有三个for循环嵌套，最外面的大循环是为了保证所有顶点都已经找到了最小路径

第二层循环。。。哎呀我好困啊明天再写吧今天就这样吧，具体的可以看看注释能不能看懂

3.非递归算法如下，思路源自于大话数据结构

#include

using namespace std;
const int MaxDist  = 65535;
class Map {
	int** matrix;
	int v0, min, vnum;//min为最小值
public:
	~Map() { delete[] matrix;}
	void SetMatrix();
	void ShortestPath_Dijkstra();
};

void Map::SetMatrix() {
	cin >> vnum;
	matrix = new int* [vnum]; 
	for (int i = 0; i < vnum; i++)
	{
		matrix[i] = new int[vnum];
		for (int j = 0; j < vnum; j++)
		{
			cin >> matrix[i][j]; //初始化数组
		}
	}
	cin >> v0;//输入起始结点

	for (int i = 0; i < vnum; i++)
	{
		for (int j = 0; j < vnum; j++)
		{
			if (matrix[i][j] == 0 && i != j)
				matrix[i][j] = MaxDist;
		}
	}
	
}

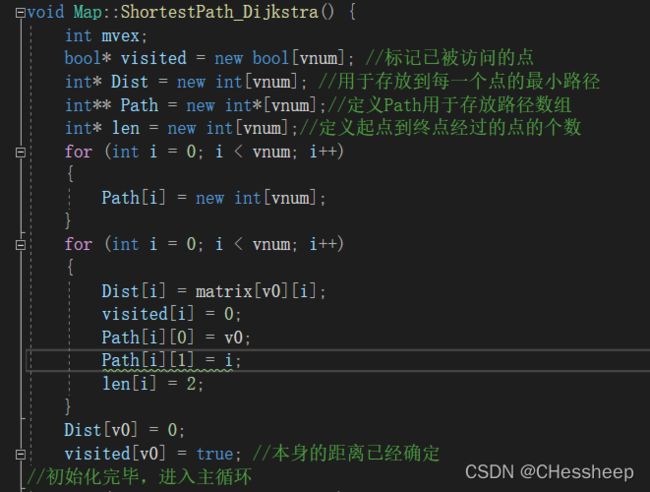
void Map::ShortestPath_Dijkstra() {
	int mvex;
	bool* visited = new bool[vnum]; //标记已被访问的点
	int* Dist = new int[vnum]; //用于存放到每一个点的最小路径
	int** Path = new int*[vnum];//定义Path用于存放路径数组
	int* len = new int[vnum];//定义起点到终点经过的点的个数
	for (int i = 0; i < vnum; i++)
	{
		Path[i] = new int[vnum];
	}
	for (int i = 0; i < vnum; i++)
	{
		Dist[i] = matrix[v0][i];
		visited[i] = 0;
		Path[i][0] = v0;
		Path[i][1] = i;
		len[i] = 2;
	}
	Dist[v0] = 0;
	visited[v0] = true; //本身的距离已经确定
//初始化完毕，进入主循环
	for (int i = 0; i < vnum; i++)
	{
		min = MaxDist;
		for (int j = 0; j < vnum; j++)
		{
			if (!visited[j] && Dist[j] < min) {
				mvex = j;
				min = Dist[j];
			}
			if (min == MaxDist) //如果该点的所有路径都被访问过了，表示无法再走下去了
				break;
			else
				visited[mvex] = true;
			for (int j = 0; j < vnum; j++)
			{
				if (!visited[j] && matrix[mvex][j] + min < Dist[j]) //若该点未被访问，而且前面的最小值加上这个点的路径小于当前路径
				{  //这里的j表示可能成为最小路径的点
					Dist[j] = matrix[mvex][j] + min; 
					for (int p = 0; p < len[mvex]; p++)
					{
						Path[j][p] = Path[mvex][p];  //将前面这一个点的路径赋给它
					}
					len[j] = len[mvex] + 1; //更换了前面的路径后，这个1 代表自己的点
					Path[j][len[mvex]] = j; //更新当前路径的终点 （就是自己）
				}
			}
			    
		}
	}
//输出
	for (int i = 0; i < vnum; i++)
	{
		if (i != v0 && Dist[i]!=MaxDist) {
			cout << v0 << '-' << i << '-' << Dist[i] << "----[";
			for (int p = 0; p < len[i]; p++)
			{
				cout << Path[i][p] << ' ';
			}
			cout << ']' << endl;
		}
	}
	delete[]visited,Dist;
	delete[]Path;
}

int main() {
	int t;
	cin >> t;
	while (t--) {
		Map mymap;
		mymap.SetMatrix();
		mymap.ShortestPath_Dijkstra();
	}
}

我自己写过一个递归算法，但是写得实在是太丑陋太冗长了，而且好像总有些小bug，要看的也可以拿去（当时觉得递归实现可以挺简洁的，结果后来一堆问题层出不穷，改了快一周的代码才勉强能用）

#include
#include
using namespace std;
const int MaxDist = 65535;

class Map {
	int** matrix;
	queue PathQue;//用来存放最短路径经过的点
	int Headvex, min, vnum;//sumadj表示每次计算路径的和，min为最小值
	void deepFound(int start, int end, int sumadj, queue TemPQ, int* visited);
public:
	~Map() { delete[] matrix; }
	void SetMatrix(int num);
	void ShortestPath_Dijkstra();
};

void Map::SetMatrix(int num) {
	matrix = new int* [num]; //开辟空间
	vnum = num;
	for (int i = 0; i < num; i++)
	{
		matrix[i] = new int[num];
		for (int j = 0; j < num; j++)
		{
			cin >> matrix[i][j]; //初始化数组
		}
	}
	cin >> Headvex;//输入起始结点

}

void Map::ShortestPath_Dijkstra() {

	for (int big = 0; big < vnum; big++) //大循环，求起始点到某个顶点的最小路径
	{
		min = MaxDist; //初始化路径最小值
		int tempmin, Tailvex;
		if (big != Headvex)
		{
			Tailvex = big;  //定义终点

			//起点和终点已经确定
			for (int i = 0; i < vnum; i++) //遍历当前行的所有路径
			{
				int sumadj = 0;
				int* visited = new int[vnum];
				for (int j = 0; j < vnum; j++)
				{
					visited[j] = 0;
				}
				visited[Headvex] = 1;
				queueTemPQ;
				while (!TemPQ.empty())
					TemPQ.pop(); //每次寻找新的路径时先清空,这个用于暂时存储路径，符合条件就替换
				if (matrix[Headvex][i] && matrix[Headvex][i] + sumadj < min && !visited[i]) //满足该路径存在而且该路径加上前面的路径小于min 
				{
					sumadj += matrix[Headvex][i];
					if (i == Tailvex) { //找到了终点

						visited[i] = 0;//终点可以被多次访问
						if (sumadj < min)
						{
							TemPQ.push(i);
							min = sumadj;
							PathQue = TemPQ; //找到了终点则将临时存储的路径赋予
						}
					}
					else {
						TemPQ.push(i);
						visited[i] = 1;
						deepFound(i, Tailvex, sumadj, TemPQ, visited); //未到终点则继续深入循环
					}
				}
			}
			//输出结果
			if (min != MaxDist) {
				cout << Headvex << '-' << Tailvex << '-';
				cout << min << "----[" << Headvex << ' ';
				while (!PathQue.empty()) {
					cout << PathQue.front() << ' ';
					PathQue.pop();
				}
				cout << ']' << endl;
			}
		}
	}
}

void Map::deepFound(int start, int end, int sumadj, queue TemPQ, int* visited) {

	for (int i = 0; i < vnum; i++) //遍历当前行的所有路径
	{
		int* TemVisit = visited;
		queue TPQ2 = TemPQ;//同理同下
		int tempSum = sumadj; //用来临时存放sumadj的变量，为了防止跳出递归后sumadj的值不会恢复
		if (matrix[start][i] && matrix[start][i] + tempSum < min && !TemVisit[i]) //满足该路径存在而且该路径加上前面的路径小于min 
		{
			tempSum += matrix[start][i];
			if (i == end) { //找到了终点

				TemVisit[i] = 0;//终点可以被多次访问
				if (tempSum < min)
				{
					TPQ2.push(i);
					min = tempSum;
					PathQue = TPQ2; //找到了终点则将临时存储的路径赋予
				}
			}
			else {
				TemVisit[i] = 1;
				TPQ2.push(i);
				deepFound(i, end, tempSum, TPQ2, TemVisit);
			}
		}
	}
}

int main() {
	int t;
	cin >> t;
	while (t--) {
		int vnum;
		cin >> vnum;
		Map mymap;
		mymap.SetMatrix(vnum);
		mymap.ShortestPath_Dijkstra();
	}
}