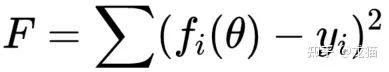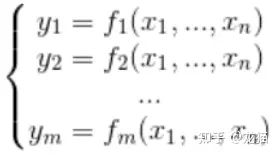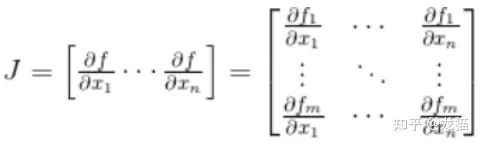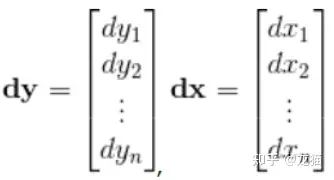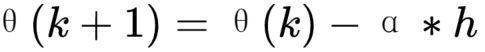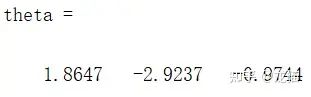【Matlab】LM迭代估计法

简介

在最近的传感器校准算法学习中，有一些非线性的代价函数求解使用最小二乘法很难求解，使用LM算法求解会简单许多，因此学习了一下LM算法的基础记录一下。

LM 优化迭代算法时一种非线性优化算法，可以看作是梯度下降与高斯牛顿法的结合，综合了两者的优点。

对于一个最小二乘的问题，如下：

其中 y(i) 为第 i 组数据的真实值或理论真实值，fi(θ) 为第 i 组数据的预测值，目的就是找到一组 θ，使得代价函数达到最小值。通常，需要指定一个初始 θ0，不断优化迭代，产生 θ1，θ2 ，最终收敛到最优值 θ。

在收敛的过程中，需要两个参数，收敛方向与收敛步长：

h 为收敛方向

α 为收敛步长

雅可比矩阵

在后续 LM 的迭代计算中，需要用到雅可比矩阵，雅可比矩阵的简易理解过程如下：

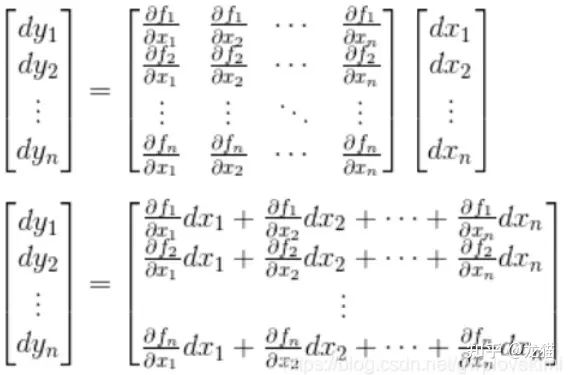
在 n 维空间中的向量，假设 x 与 y 的映射关系为 y：

以上的映射关系用 F 表示。

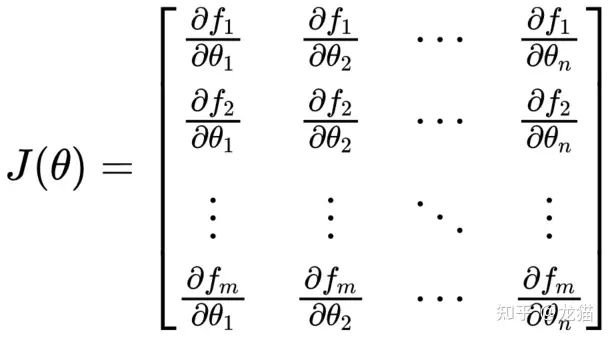
那么雅可比矩阵就可以写作：

雅可比矩阵的意义就在于，假设 p 是向量中的一个点，F 在点 p 处是可微的，那么雅可比矩阵 J(p) 就是这点的导数，定义一个 x，当 x 足够接近 p 时，就可以得到：

F(x) ≈ F(p) + J(p) * (x - p)

F(x) - F(p) ≈ J(p) * (x - p)

即：

Δy ≈ J(p) * Δx

转化为微分：

dy = J(p) dx

将上述的微分与雅可比矩阵展开：

雅可比矩阵与 LM 代价函数的关系

LM 代价函数，对 θ 求偏导，就是一个雅可比矩阵，雅可比矩阵的更新在 LM 算法中，非常关键。

LM算法的步骤

LM算法的迭代公式

LM算法的迭代可以理解为结合了梯度下降与高斯牛顿的优点，因此其迭代公式可以对比观察。

梯度下降

dot(J) 就是 J 的一阶倒数

高斯牛顿

高斯牛顿在牛顿迭代的基础上，使用了雅可比矩阵的平方，使得求解更快，但如果初始值不在最优解附近，则求解就可能出错：

f 表示代价函数中的残差，J 表示雅可比矩阵

LM算法

由于 J_T*J 在某些情况下是不可逆的，因此 LM 增加了一个系数 λ*I (I 为单位矩阵) ，以此来保证等式左边是一定可逆的，就可以求解所有的情况：

1）当 λ 设置的比较大时，就相当于是梯度下降，适合当前的估计参数距离最优解比较远的情况

2）当 λ 设置的比较小时，就相当于高斯牛顿，适合估计参数距离最优解比较近的情况

因此在 LM 算法中，需要根据情况来调整 λ 的值来得到最优解

步骤

通常遵循以下步骤：

1.采样n组数据，定义代价函数，如下所示：

fi 表示模型对第 i 个样本的预测值， y 表示真实值或者理论真实值。

2.初始化参数向量，需要初始化模型的估计参数 θ，可以随机初始化或根据经验设置初值

3.计算雅可比矩阵，即代价函数关于估计参数向量 θ 的雅可比矩阵：

4.计算初始代价函数值，将初始估计参数 θ 带入

5.设置 LM 算法的参数，包括初始阻尼因子 λ ，最大迭代次数，迭代精度，收敛步长等

6.迭代更新参数向量，雅可比矩阵(有一些简单的情况雅可比矩阵只与采样值有关，就可以只计算一次)，这里将收敛补偿设置为1，即α = 1

之后更新新的估计参数：

并使用新的估计参数带入代价函数 F，计算新的代价函数是否更小，如果更小则接受更新，否则，拒绝更新，并增大 λ：

λ = 10 * λ

如果新的参数更优，则将 λ 减小：

λ = 0.1 * λ

7.更改估计参数之后，再次使用 n 组采样数据，重复 6 步骤，如果代价函数值变化小于设定的迭代精度，或达到最大迭代次数，则停止迭代，返回跌代后的参数向量 θ

使用多项式拟合例子验证

假设需要拟合一个二次多项式 f = a * x^2 + b * x + c，假设真实的多项式参数 a = 2，b = -3，c = -1，之后添加随机噪声。

按照 LM 算法的步骤，定义初始的参数估计矩阵为：

theta = [1,1,1]

收敛步长 alpha 定义为1，不变

迭代次数为 1000 次，采样 100 组 x，y 数据。

之后按照这个简化步骤，就可以迭代计算出多项式的值：

1）更新雅可比矩阵

2）计算迭代步长 h

3）判断是否更新估计参数(根据新的代价值是否变得更小)，如果要更新，则将迭代步长加到上一次的估计参数矩阵 theta 中，并减小 lambda ；反之，则拒绝更新，并加大 lambda

(lambda 越小，越适合接近最优解的时候，lambda越大，越适合距离最优解较远的时候)

更新雅可比矩阵

针对此例子，雅可比的通式为：

其中，n 表示估计参数矩阵的维度，m 表示采样次数，f 表示代价函数中的预测方程：

计算之后，此多项式的雅可比矩阵为：

只是恰好这个例子的雅可比矩阵偏导求解出来是不包含代预估变量的，可以只更新一次，正常是每次迭代都需要更新的。

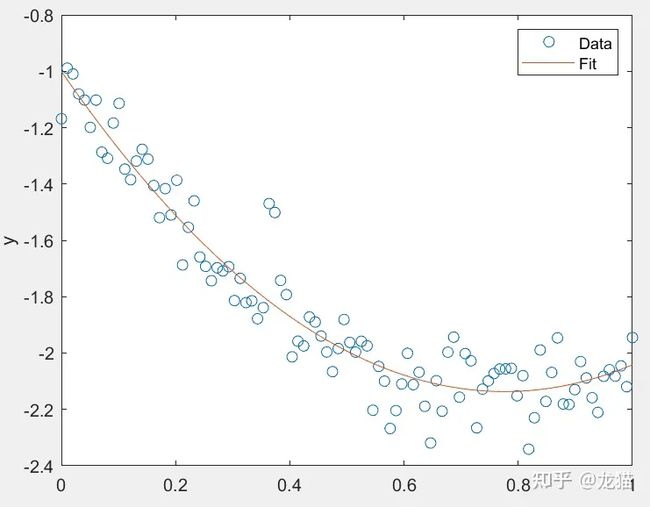
最终的拟合效果如下：

拟合出的估计参数与实际值也是接近的