聚类分析——SPSS实例分析

操作使用数据情况如下：

表1  2022年中国31个省份增加值指标

地区	工业增加值	建筑业增加值	农林牧渔业增加值	金融业增加值	交通运输、仓储和邮政业增加值
江苏省	48593.6	7377.8	5369.5	9689.9	3655.6
山东省	28739	6424.5	6769	5203.1	4911
河南省	19592.8	5951.6	6169.8	3301.4	3721.1
福建省	19628.8	5518.9	3191.9	3889.8	1960
广东省	47723	5247.6	5531.6	11825.8	4040.9
四川省	16412.2	4888.6	6133.1	3840.1	1587.5
安徽省	13792	4819.4	3722.3	2935.1	2171.7
浙江省	28871.3	4388.1	2397	6690	2375.5
湖南省	15025.3	4174.9	4873.4	2421.5	1696.9
湖北省	17546.3	3741.6	5321.9	3639.7	2313.9
重庆市	8276	3417.9	2058.6	2491	1084
云南省	7197.1	3282.4	4090.1	1594.6	1335.4
陕西省	13158.3	2893	2710.6	2109.7	1293.8
江西省	11770.3	2597.2	2577.8	2140.5	1341.7
河北省	14675.3	2413.6	4697.4	2931.8	3013.3
广西壮族自治区	6775.9	2180.4	4404.2	1834.7	1098.3
贵州省	5493.1	1626.2	3020.4	1193.5	838.2
北京市	5036.4	1614.2	113.2	8196.7	879.2
辽宁省	10239.1	1598.7	2685.8	2138.3	1367.6
内蒙古自治区	9703.9	1538	2710	981.7	1317.9
新疆维吾尔自治区	6022.8	1355.7	2654.6	1216.9	845.3
山西省	12758.6	1093.3	1415.4	1359	1198.5
吉林省	3737.9	927.2	1742.3	1000.4	592.1
上海市	10794.5	743.6	104.9	8626.3	1914.5
天津市	5402.7	724.7	283.4	2197.3	1061.1
甘肃省	3297.2	657.6	1561.3	925.1	555.6
西藏自治区	200.8	603.9	185	215.4	42.5
海南省	770.1	545.6	1471.4	438.7	371.9
黑龙江省	4257.6	460.3	3710.9	1127.2	553.1
宁夏回族自治区	2094	357.2	428.6	352.2	213.5
青海省	1228.7	357	385	286.2	155.2

一、系统聚类法(层次聚类法)

在SPSS数据窗口中录入上表中的数据，然后选择 Analyze - Classify 命令， Classify 命令下有两个常用的聚类分析命令。此处我们选择系统聚类法，并打开相应的对话框，然后将5个指标变量选入 Variable 框中，将表示省份的变量选入 Label Cases by 框中。在下面的 Cluster 中有两个选项，分别是 Cases （表示对样品聚类或 Q 型聚类）和 Variables （表示对变量聚类或 R 型聚类）。这里，我们点选 Cases ，选择对样品进行聚类。 Display 部分也有两个选项，分别是 Statistics （统计量）和 Plots （图），即可以选择输出统计量或图形，或二者均输出，此处选择二者均输出。

在对话框的最右侧有 Statistics , Plots , Method , Save 四个按钮：

（1）Statistics 中有 Agglomeration schedule （每一阶段聚类的结果） Proximity matrix （样品间相似性矩阵），还有 Cluster Membership 。 Cluster Membership 框架下可以指定聚类的个数， None 选项为不指定聚类个数， Single solution 为指定一个确定的聚类个数（如3)， Range of solutions 为指定聚类个数的范围（如2~4）。

（2） Plots 中有 Dendrogram （谱系聚类图或树状聚类图）、 Icicle （冰柱图）、 Orientation （冰柱图的方向， Horizontal 为水平方向， Vertical 为垂直方向）。此处我们选择 Horizontal ，点击 Continue 继续。

（3）Method 中， Cluster Method 可以选择聚类的方法（如最短距离法或离差平方和方法等）， Measure 可以选择距离的计算方法（如欧氏距离或明考斯基距离等）， Transform Values 可以选择是否对数据进行处理及相应的处理方法。此处我们选择 Within - groups linkage （组内联结法）和平方欧氏距离，并选择 Z scores （对数据进行标准化处理），点击 Continue 继续。

（4）Save 中可以选择保存样本的聚类结果，此处我们选择保存样本被聚为5类的结果。点击 Save ，在弹出对话框中点选 Single solution ，然后在其下方 Number of clusters 右侧的框中填入5，点击 Continue 继续，点击 OK 运行。运行结束后，数据窗口（ Data View ）中将会多出一个变量名为CLU5_1的新变量，此变量的取值即为将所有样品聚为5类时应得的分类结果。

选定聚类的方法和需要输出的图表后，点击 OK 运行，则可得到一系列输出结果如下。

表2 个案处理摘要

个案
有效		缺失		总计
个案数	百分比	个案数	百分比	个案数	百分比
31	100.0%	0	0.0%	31	100.0%
a.  平方欧氏距离 使用中

表1-1为个案处理摘要，本例个案共31个。

表3 集中计划

阶段	组合聚类		系数	首次出现聚类的阶段		下一个阶段
	聚类 1	聚类 2		聚类 1	聚类 2
1	29	30	.009	0	0	4
2	7	28	.028	0	0	6
3	14	27	.040	0	0	8
4	26	29	.042	0	1	11
5	24	31	.053	0	0	9
6	7	21	.104	2	0	11
7	5	6	.158	0	0	9
8	14	22	.267	3	0	18
9	5	24	.283	7	5	12
10	20	25	.359	0	0	18
11	7	26	.394	6	4	15
12	4	5	.487	0	9	16
13	12	13	.562	0	0	21
14	17	18	.573	0	0	17
15	2	7	.586	0	11	25
16	4	8	.714	12	0	19
17	17	23	.735	14	0	21
18	14	20	.815	8	10	19
19	4	14	1.097	16	18	22
20	1	9	1.173	0	0	27
21	12	17	1.244	13	17	24
22	3	4	1.626	0	19	25
23	10	19	1.711	0	0	30
24	12	16	2.077	21	0	26
25	2	3	2.491	15	22	27
26	11	12	2.856	0	24	28
27	1	2	3.562	20	25	29
28	11	15	4.366	26	0	29
29	1	11	7.054	27	28	30
30	1	10	10.000	29	23	0

表3是对每一阶段聚类结果的展示，其中 Coefficients 表示聚类系数，表中第2列和第3列表示聚合的类。比如第一阶段，第29个样本和第30个样本聚为一类，注意此时有30类（31-1=30）。因此，某阶段的分类数等于总的样本数减去这个阶段的序号。

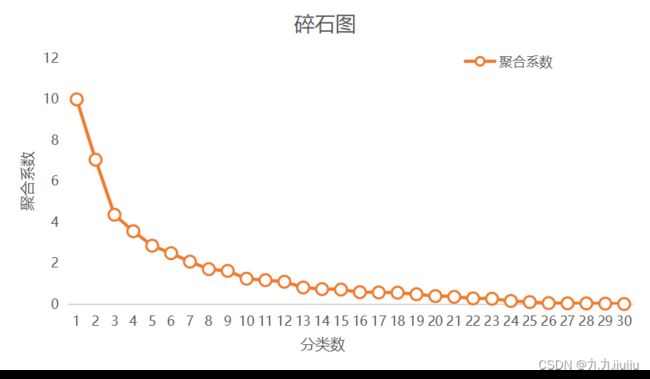
图1 碎石图

另外，使用 Excel 作出表3中的聚合系数随分类数变化的曲线，如上图可知，当分类数大于5时，曲线的变化趋势较为平缓，同时此分类数也较符合分类的目的。

 

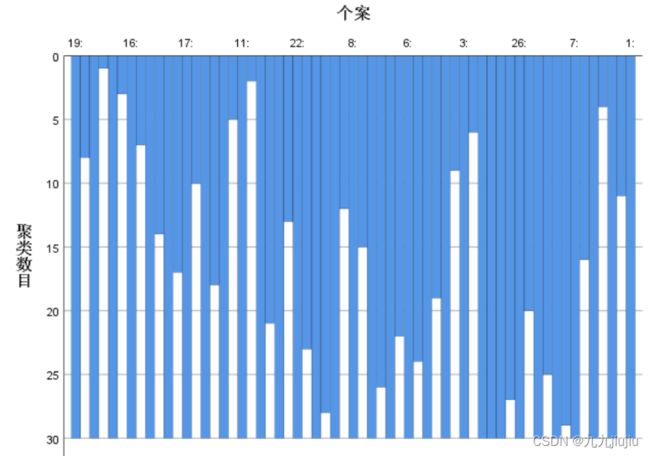
图2 冰柱图

图2为冰柱图，是反映样品聚类情况的图形，冰柱图形象地展示了聚类的动态过程。

对于纵向的冰柱图可以自下而上看出聚类的过程，首先，从最下面看，代表青海和宁夏的两条冰柱之间的冰柱最长，它对应的类数是30，表示青海和宁夏先被聚为一类。其次是吉林与甘肃之间的冰柱长度，对应的类数是29，则第二步吉林与甘肃被聚为一类。同理，第三步江西与陕西被聚为一类，此时共有28类。第四步西藏与青海被聚为一类，即西藏、青海和宁夏被聚为一类，此时共有27类。依此类推，直至冰柱长度对应的类数为1时，将北京所在的类和江苏所在的类聚在一起成为一个类。另外，对于给定的类数，若要从冰柱图中得知每类所包含的样本，只需找到长度小于对应该给定类数的冰柱。然后，以这些冰柱为分隔点，从左起至第一个分隔点之间的样品为一类，第一个与第二个分隔点之间的样品为第二类，依此类推，直至最后一个分隔点至最右边为最后一类。

例如，对于图2，若设定类数为5，则需要找到冰柱长度对应类数小于5的冰柱，它们是江苏与广东之间的冰柱、北京与上海之间的冰柱、浙江与重庆之间的冰柱、山东为单独一类、其余各省为一类。

 

图3 树状聚类图

图3为树状聚类图，从该图可以由分类个数得到分类情况，如果选择类数为5，就从距离大概为8的地方往下切，得到的分类结果如上面冰柱图中举例所述。江苏和广东聚为一类；山东是单独的一类；浙江、安徽、福建、河南、湖北、湖南、重庆聚为一类；北京和上海聚为一类；剩下的各省均为一类。从农林牧渔业增加值和交通运输业增加值来看，山东省位于全国第1位，因此被单独分为一类。而第二类（江苏省和广东省）对应的工业增加值和建筑业增加值水平较高，其中广东省的金融业增加值最高。第三类（北京市和上海市）对应的金融业增加值较高，农林牧渔业增加值最低，因此将二者分为一类。

二、快速聚类法（K-means）

同样，我们采用表1中的数据，试图将31个省份使用快速聚类法（ K - Means Cluster ）对样品进行聚类。由于原始数据的量纲一致，因此不需要对数据进行标准化。

在 SPSS 软件中选择 Analyze → Classify → K - Means Cluster ，打开 K-均值聚类对话框，然后将5个指标变量选入 Variables 框，并将表示省份的变量选入 Label Cases by 框。将分类数（ Number of Clusters ）设为5，点击对话框右侧的 Options 选项并打开对话框，然后选择 Initial cluster centers （初始分类中心）、 ANOVA table （方差分析表）、 Cluster information for each case （每个样品的分类信息），点击 Continue 继续，点击 OK 运行，可得到如下结果。

表4 初始聚类中心

	聚类
	1	2	3	4	5
工业	5036	201	28739	48594	16412
建筑	1614	604	6425	7378	4889
农业	113	185	6769	5370	6133
金融	8197	215	5203	9690	3840
交通运输	879	43	4911	3656	1588

输出结果中，表4列出了初始各类的中心，也就是种子点。

表5 样本的分类情况

个案号	地区	聚类	距离
1	北京	1	6803.870
2	天津	2	2864.987
3	河北	5	2579.200
4	山西	1	4243.398
5	内蒙	1	2434.565
6	辽宁	1	1665.755
7	吉林	2	565.741
8	黑龙	2	2419.486
9	上海	1	6160.917
10	江苏	4	1583.706
11	浙江	3	2824.821
12	安徽	5	2650.377
13	福建	5	3959.030
14	江西	1	2910.944
15	山东	3	2824.821
16	河南	5	4333.764
17	湖北	5	1682.280
18	湖南	5	1522.561
19	广东	4	1583.706
20	广西	1	3539.698
21	海南	2	2536.836
22	重庆	1	1860.295
23	四川	5	1902.963
24	贵州	2	2853.807
25	云南	1	3425.713
26	西藏	2	3444.723
27	陕西	5	4110.231
28	甘肃	2	123.434
29	青海	2	2470.101
30	宁夏	2	1770.979
31	新疆	2	3078.786

表5是样品的分类情况。这里我们看到快速聚类法将31个省份分为五类。分别是1：{北京，山西，内蒙，辽宁，上海，江西，广西，重庆，云南}； 2：{天津，吉林，黑龙江，海南，贵州，西藏，甘肃，青海，宁夏，新疆}； 3：{山东，浙江}； 4：{江苏，广东}； 5{河北，安徽，福建，河南，湖北，湖南，四川，陕西}。该结果与系统聚类的结果略有不同，但大体一致。

表6 最后各类的中心

	聚类
	1	2	3	4	5
工业	9172	3250	28805	48158	16229
建筑	2007	762	5406	6313	4300
农业	2240	1544	4583	5451	4603
金融	3263	895	5947	10758	3134
交通运输	1282	523	3643	3848	2220

表6是样品的最后聚类中心情况。

表7 方差分析表

ANOVA
	聚类		误差		F	显著性
	均方	自由度	均方	自由度
工业	1034260063.788	4	5190653.652	26	199.254	.000
建筑	25782544.139	4	909038.113	26	28.362	.000
农业	15987109.875	4	2074052.426	26	7.708	.000
金融	45582443.940	4	3059529.523	26	14.899	.000
交通运输	8511223.792	4	362426.149	26	23.484	.000
由于已选择聚类以使不同聚类中个案之间的差异最大化，因此 F 检验只应该用于描述目的。实测显著性水平并未因此进行修正，所以无法解释为针对“聚类平均值相等”这一假设的检验。

表7为方差分析表，但是应该注意F值只能作为描述使用，不能根据该值判断各类均值是否有显著差异。另外，从方差分析表可以看出，这5个变量对分类的贡献均显著。