极大似然估计法及其损失函数的优化方法

二分类-逻辑回归模型

1.建立模型：二分类逻辑回归模型

1.1 模型函数

1）多元线性回归函数：${\hat{Z}}_{计算}=X{W}^T$
2）sigmoid函数：${\hat{Y}}_{模型}=Sigmoid({\hat{Z}}_{计算})=\frac{1}{1+e^{-{\hat{Z}}_{计算}}}$
已知数据：实际Y值= [ y 0 y 1 y 2 y 3 . . . y n ] \begin{bmatrix}y_0\\y_1\\y_2\\y_3\\...\\y_n\end{bmatrix} ​y0​y1​y2​y3​...yn​​ ​ ，X= [ x 00 , x 10 . . . x m 0 x 01 , x 11 . . . x m 1 x 02 , x 12 . . . x m 2 x 03 , x 13 . . . x m 3 . . . x 0 n , x 1 n . . . x m n ] \begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix} ​x00​,x10​...xm0​x01​,x11​...xm1​x02​,x12​...xm2​x03​,x13​...xm3​...x0n​,x1n​...xmn​​ ​
未知数据：有如下3组未知数据
①模型参数 W = $\left[\begin{array}{c}{w}_0,w_1,w_2,w_3,...,w_m\end{array}\right]$
②线性函数计算 Z ^ 计算 = X W T = [ x 00 , x 10 . . . x m 0 x 01 , x 11 . . . x m 1 x 02 , x 12 . . . x m 2 x 03 , x 13 . . . x m 3 . . . x 0 n , x 1 n . . . x m n ] [ w 0 w 1 w 2 w 3 . . . w m ] = [ z 0 ^ z 1 ^ z 2 ^ z 3 ^ . . . z n ^ ] \hat{Z}_{计算}=XW^T=\begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix}\begin{bmatrix}w_0\\w_1\\w_2\\w_3\\...\\w_m\end{bmatrix}=\begin{bmatrix}\hat{z_0}\\\hat{z_1}\\\hat{z_2}\\\hat{z_3}\\...\\\hat{z_n}\end{bmatrix} Z^计算​=XWT= ​x00​,x10​...xm0​x01​,x11​...xm1​x02​,x12​...xm2​x03​,x13​...xm3​...x0n​,x1n​...xmn​​ ​ ​w0​w1​w2​w3​...wm​​ ​= ​z0​^​z1​^​z2​^​z3​^​...zn​^​​ ​

③模型分类 Y ^ = S i g m o i d ( Z ^ ) = [ 1 1 + e − z 0 ^ 1 1 + e − z 1 ^ 1 1 + e − z 2 ^ 1 1 + e − z 3 ^ . . . 1 1 + e − z n ^ ] = [ y 0 ^ y 1 ^ y 2 ^ y 3 ^ . . . y n ^ ] \hat{Y}=Sigmoid(\hat{Z})=\begin{bmatrix} \frac{1}{1+e^{-\hat{z_0}}}\\\frac{1}{1+e^{-\hat{z_1}}}\\\frac{1}{1+e^{-\hat{z_2}}}\\\frac{1}{1+e^{-\hat{z_3}}}\\...\\\frac{1}{1+e^{-\hat{z_n}}}\end{bmatrix}=\begin{bmatrix}\hat{y_0}\\ \hat{y_1}\\\hat{y_2}\\\hat{y_3}\\...\\\hat{y_n}\end{bmatrix} Y^=Sigmoid(Z^)= ​1+e−z0​^​1​1+e−z1​^​1​1+e−z2​^​1​1+e−z3​^​1​...1+e−zn​^​1​​ ​= ​y0​^​y1​^​y2​^​y3​^​...yn​^​​ ​

1.1 理解Sigmoid函数

逻辑分布的来源：震惊!!!逻辑分布与逻辑关系不大(B站)

一个事件的几率，是事件发生与不发生的概率比值：$O=\frac{P}{1-P}$，O是个指数函数$e^x$，值在0到+∞范围
$O=\frac{P}{1-P}=e^x$，求出P $P=\frac{1}{1+e^{-x}}$，因此P表示事件发生的概率，1-P就是事件不发生的概率

此时，P的值随x值增大而增大：当x值越大，事件发生的概率P越大

对应到我们的二分类逻辑回归模型：
线性回归函数计算出的 $\hat{Z}$，是一个实值，我们可以通过sigmoid函数，根据$\hat{Z}$值计算出事件发生的概率
${\hat{Y}}_{模型}=Sigmoid({\hat{Z}}_{计算})=\frac{1}{1+e^{-{\hat{Z}}_{计算}}}$

${\hat{Y}}_{模型}里的值为0到1小数，例如0.4，表示事件发生（即分类为1）的概率是0.4$
那么，事件不发生（分类为0）的概率是 $1-\hat{Y}$

2. 学习模型：损失函数-二分类的极大似然估计

逻辑回归模型的损失函数，采用极大似然估计法
$Loss=-{\sum }_{i=0}^n(\widehat{y_i}.ln{y}_i+(1-\widehat{y_i}).ln{y}_i)$

2.1 理解极大似然估计法

二分类，指实际只有两种互斥的类别：要么是男，要么是女（要么A类，要么B类）
这就是个典型的0-1分布（伯努利分布）

实际分类	y=0	y=1
计算出的分类概率	$1-\hat{y}$	$\hat{y}$

单次分类正确的概率为：${\hat{y}}_{计算}^y\ast (1-{\hat{y}}_{计算}{)}^{(1-y)}$

• 实际分类为$y=1$时，分类正确的概率为${\hat{y}}_{计算}^y\ast (1-{\hat{y}}_{计算}{)}^{(1-y)}$=${\hat{y}}_{计算}^1={\hat{y}}_{计算}$
• 实际分类为$y=0$时，分类正确的概率为${\hat{y}}_{计算}^y\ast (1-{\hat{y}}_{计算}{)}^{(1-y)}$=$(1-{\hat{y}}_{计算}{)}^1=1-{\hat{y}}_{计算}$

无论实际分类是y=0还是y=1，我们都希望模型分类正确的概率达到最大！
即求出${\hat{y}}_{计算}^y\ast (1-{\hat{y}}_{计算}{)}^{(1-y)}$的最大值。

即为分类正确的概率：即为似然值——表示基于实际分布下，模型分类正确的概率值

${\hat{y}}_{计算}^y\ast (1-{\hat{y}}_{计算}{)}^{(1-y)}$，不好求极值
因此可以转化为$ln(x)$函数，因为$ln(x)$是单调递增函数，那么只要x越大，则$ln(x)$也越大。

${\hat{y}}_{计算}^y\ast (1-{\hat{y}}_{计算}{)}^{(1-y)}$变为

$ln({\hat{y}}_{计算}^y\ast (1-{\hat{y}}_{计算}{)}^{(1-y)})=yln({\hat{y}}_{计算})+(1-y)ln(1-{\hat{y}}_{计算})$

求出$yln({\hat{y}}_{计算})+(1-y)ln(1-{\hat{y}}_{计算})$的最大值即可，这正是极大似然估计法的核心思想

但我们习惯转化为损失函数Loss，求损失函数Loss的极小值，因此可在函数前加负号即可：

$Loss=-[yln({\hat{y}}_{计算})+(1-y)ln(1-{\hat{y}}_{计算})]$，求出Loss的极小值，即可使单次分类正确率达到最大

那么，要使所有分类的正确率达到最大，即将每次分类的Loss值累加：

$Los{s}_{总}=-{\sum }_{i=0}^{n}yln({\hat{y}}_{计算})+(1-y)ln(1-{\hat{y}}_{计算})$

2.2 损失函数优化方法

2.2.1 求导-解析解

$Loss=-{\sum }_{i=0}^{n}yln({\hat{y}}_{计算})+(1-y)ln(1-{\hat{y}}_{计算})$
$\frac{d(Loss)}{d(W)}=\frac{y}{{\hat{y}}_{计算}}\ast \frac{d({\hat{y}}_{计算})}{dw}-\frac{(1-y)}{1-{\hat{y}}_{计算}}\ast \frac{d({\hat{y}}_{计算})}{dw}$________太复杂了，放弃

逻辑回归模型，通常用的是迭代-近似解的方式，求解Loss极小值

2.2.2 迭代-近似解

梯度下降法 or 拟牛顿法

多分类-逻辑回归模型

1. 模型函数

1）多元线性回归函数：${\hat{Z}}_{计算}=X{W}^T$
2）softmax函数：${\hat{Y}}_{模型}=softmax({\hat{Z}}_{计算})=\frac{1}{1+e^{-{\hat{Z}}_{计算}}}$

已知数据：实际Y值= [ y 0 y 1 y 2 y 3 . . . y n ] \begin{bmatrix}y_0\\y_1\\y_2\\y_3\\...\\y_n\end{bmatrix} ​y0​y1​y2​y3​...yn​​ ​ ，需要转为独热编码 Y值= [ y 00 , y 01 , . . . , y 0 k y 10 , y 11 , . . . , y 1 k y 20 , y 21 , . . . , y 2 k . . . y n 0 , y n 1 , . . . , y n k ] \begin{bmatrix}{y_{00}},{y_{01}},...,{y_{0k}}\\ \\{y_{10}},{y_{11}},...,{y_{1k}}\\\\ {y_{20}},{y_{21}},...,{y_{2k}}\\\\...\\\\ {y_{n0}},{y_{n1}},...,{y_{nk}}\end{bmatrix} ​y00​,y01​,...,y0k​y10​,y11​,...,y1k​y20​,y21​,...,y2k​...yn0​,yn1​,...,ynk​​ ​

X= [ x 00 , x 10 . . . x m 0 x 01 , x 11 . . . x m 1 x 02 , x 12 . . . x m 2 x 03 , x 13 . . . x m 3 . . . x 0 n , x 1 n . . . x m n ] \begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix} ​x00​,x10​...xm0​x01​,x11​...xm1​x02​,x12​...xm2​x03​,x13​...xm3​...x0n​,x1n​...xmn​​ ​

未知数据： 如果原数据共有 k+1 个类别，则有如下未知数据
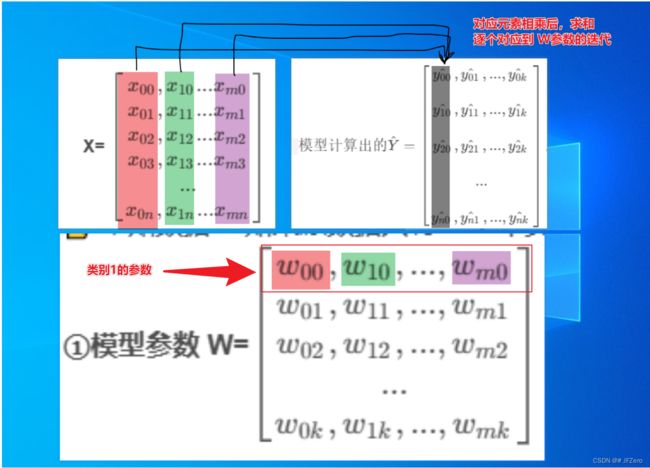
①模型参数 W= [ w 00 , w 10 , . . . , w m 0 w 01 , w 11 , . . . , w m 1 w 02 , w 12 , . . . , w m 2 . . . w 0 k , w 1 k , . . . , w m k ] \begin{bmatrix}w_{00},w_{10},...,w_{m0}\\w_{01},w_{11},...,w_{m1}\\w_{02},w_{12},...,w_{m2}\\...\\w_{0k},w_{1k},...,w_{mk}\end{bmatrix} ​w00​,w10​,...,wm0​w01​,w11​,...,wm1​w02​,w12​,...,wm2​...w0k​,w1k​,...,wmk​​ ​

②计算 Z ^ n × k = X ( n × m ) W m × k T = [ z 00 ^ , z 01 ^ , . . . , z 0 k ^ z 10 ^ , z 11 ^ , . . . , z 1 k ^ z 20 ^ , z 21 ^ , . . . , z 2 k ^ . . . z n 0 ^ , z n 1 ^ , . . . , z n k ^ ] \hat{Z} _{n×k}= {X_{(n×m)}W^T_{m×k}}=\begin{bmatrix}\hat{z_{00}},\hat{z_{01}},...,\hat{z_{0k}}\\ \hat{z_{10}},\hat{z_{11}},...,\hat{z_{1k}}\\\hat{z_{20}},\hat{z_{21}},...,\hat{z_{2k}}\\...\\\hat{z_{n0}},\hat{z_{n1}},...,\hat{z_{nk}}\end{bmatrix} Z^n×k​=X(n×m)​Wm×kT​= ​z00​^​,z01​^​,...,z0k​^​z10​^​,z11​^​,...,z1k​^​z20​^​,z21​^​,...,z2k​^​...zn0​^​,zn1​^​,...,znk​^​​ ​

③模型分类 Y ^ = S o f t m a x ( Z ) = [ e z i j ∑ j = 1 k e z i j ] = [ e z 00 ∑ j = 1 k e z 0 j , e z 01 ∑ j = 1 k e z 0 j , . . . , e z 0 k ∑ j = 1 k e z 0 j e z 10 ∑ j = 1 k e z 1 j , e z 11 ∑ j = 1 k e z 1 j , . . . , e z 1 k ∑ j = 1 k e z 1 j e z 20 ∑ j = 1 k e z 2 j , e z 21 ∑ j = 1 k e z 2 j , . . . , e z 2 k ∑ j = 1 k e z 2 j . . . e z n 0 ∑ j = 1 k e z n j , e z n 1 ∑ j = 1 k e z n j , . . . , e z n k ∑ j = 1 k e z n j ] = [ y 00 ^ , y 01 ^ , . . . , y 0 k ^ y 10 ^ , y 11 ^ , . . . , y 1 k ^ y 20 ^ , y 21 ^ , . . . , y 2 k ^ . . . y n 0 ^ , y n 1 ^ , . . . , y n k ^ ] \hat{Y}=Softmax(Z)=\begin{bmatrix}\frac{e^{z_{ij}}}{\sum_{j=1}^ke^{z_{ij}}}\end{bmatrix}=\begin{bmatrix} \frac{e^{z_{00}}}{\sum_{j=1}^ke^{z_{0j}}},\frac{e^{z_{01}}}{\sum_{j=1}^ke^{z_{0j}}},...,\frac{e^{z_{0k}}}{\sum_{j=1}^ke^{z_{0j}}}\\\\ \frac{e^{z_{10}}}{\sum_{j=1}^ke^{z_{1j}}},\frac{e^{z_{11}}}{\sum_{j=1}^ke^{z_{1j}}},...,\frac{e^{z_{1k}}}{\sum_{j=1}^ke^{z_{1j}}}\\\\ \frac{e^{z_{20}}}{\sum_{j=1}^ke^{z_{2j}}},\frac{e^{z_{21}}}{\sum_{j=1}^ke^{z_{2j}}},...,\frac{e^{z_{2k}}}{\sum_{j=1}^ke^{z_{2j}}}\\\\...\\\\ \frac{e^{z_{n0}}}{\sum_{j=1}^ke^{z_{nj}}},\frac{e^{z_{n1}}}{\sum_{j=1}^ke^{z_{nj}}},...,\frac{e^{z_{nk}}}{\sum_{j=1}^ke^{z_{nj}}}\\ \end{bmatrix}= \begin{bmatrix}\hat{y_{00}},\hat{y_{01}},...,\hat{y_{0k}}\\ \\\hat{y_{10}},\hat{y_{11}},...,\hat{y_{1k}}\\\\ \hat{y_{20}},\hat{y_{21}},...,\hat{y_{2k}}\\\\...\\\\ \hat{y_{n0}},\hat{y_{n1}},...,\hat{y_{nk}}\end{bmatrix} Y^=Softmax(Z)=[∑j=1k​ezij​ezij​​​]= ​∑j=1k​ez0j​ez00​​,∑j=1k​ez0j​ez01​​,...,∑j=1k​ez0j​ez0k​​∑j=1k​ez1j​ez10​​,∑j=1k​ez1j​ez11​​,...,∑j=1k​ez1j​ez1k​​∑j=1k​ez2j​ez20​​,∑j=1k​ez2j​ez21​​,...,∑j=1k​ez2j​ez2k​​...∑j=1k​eznj​ezn0​​,∑j=1k​eznj​ezn1​​,...,∑j=1k​eznj​eznk​​​ ​= ​y00​^​,y01​^​,...,y0k​^​y10​^​,y11​^​,...,y1k​^​y20​^​,y21​^​,...,y2k​^​...yn0​^​,yn1​^​,...,ynk​^​​ ​

问题： 模型计算出的 Y ^ = [ y 00 ^ , y 01 ^ , . . . , y 0 k ^ y 10 ^ , y 11 ^ , . . . , y 1 k ^ y 20 ^ , y 21 ^ , . . . , y 2 k ^ . . . y n 0 ^ , y n 1 ^ , . . . , y n k ^ ] 模型计算出的 \hat{Y} =\begin{bmatrix}\hat{y_{00}},\hat{y_{01}},...,\hat{y_{0k}}\\ \\\hat{y_{10}},\hat{y_{11}},...,\hat{y_{1k}}\\\\ \hat{y_{20}},\hat{y_{21}},...,\hat{y_{2k}}\\\\...\\\\ \hat{y_{n0}},\hat{y_{n1}},...,\hat{y_{nk}}\end{bmatrix} 模型计算出的Y^= ​y00​^​,y01​^​,...,y0k​^​y10​^​,y11​^​,...,y1k​^​y20​^​,y21​^​,...,y2k​^​...yn0​^​,yn1​^​,...,ynk​^​​ ​，实际独热编码 Y值= [ y 00 , y 01 , . . . , y 0 k y 10 , y 11 , . . . , y 1 k y 20 , y 21 , . . . , y 2 k . . . y n 0 , y n 1 , . . . , y n k ] \begin{bmatrix}{y_{00}},{y_{01}},...,{y_{0k}}\\ \\{y_{10}},{y_{11}},...,{y_{1k}}\\\\ {y_{20}},{y_{21}},...,{y_{2k}}\\\\...\\\\ {y_{n0}},{y_{n1}},...,{y_{nk}}\end{bmatrix} ​y00​,y01​,...,y0k​y10​,y11​,...,y1k​y20​,y21​,...,y2k​...yn0​,yn1​,...,ynk​​ ​，如何进行比较？极大似然估计法如何计算？？

2. 学习模型：损失函数-多分类的极大似然估计

$Los{s}_{单次}=y_{00}ln({\hat{y}}_{00})+y_{01}ln({\hat{y}}_{01})+y_{02}ln({\hat{y}}_{02})...+y_{0k}ln({\hat{y}}_{0k})={\sum }_{j=0}^k{y}_{0j}ln({\hat{y}}_{0j})$_____第一条数据的Loss值

$Los{s}_{总}={\sum }_{i=0}^n{\sum }_{j=0}^k{y}_{ij}ln({\hat{y}}_{ij})$_____总共 n+1 条数据的Loss值

3. 代码实践：手动与sklearn的代码对比

真的，原理理解起来很简单，但是实践起来，才知道bug重重，阻力重重！！！！！
尤其是对softmax的交叉熵函数求导，看了很多博主的解说，跟我的推导也是一样的！！！！
但是，推导虽然一样，但它们都不是对多维度的数组求导来解说的
大家都会先拿一个向量来解说怎么推导，但多维数组却闭口不提
啊。。。。。于是我开始自己徒手推到高维数组的求导计算过程
我。。。生活如此美好，我却总干消磨时间、毫无价值的事情
让自己变得满腹牢骚
还好，最后终于”徒手“推出来了
不管对不对，至少能够顺利迭代了，我爱我自己

3.1 重难点：softmax的交叉熵函数求导

希望日后看到这个草稿，我还能从缭乱中，找到我的思路【大概率是不可能的，除非见鬼】

其实，级联求导是很简单的，但难点在于，对多维数组求导，矩阵到底是怎么个计算过程。
还是好好梳理一下。
求导后的公式是：$\frac{d(Loss)}{dw}=\Sigma Y\ast (\hat{Y}-1)\ast X$
问题来了，在实际计算时这里的*，其实是对应位置的元素相乘

• 首先，$Y\ast (\hat{Y}-1)$对应元素相乘后，数组形状没变，还是nxk，n条数据，k种类型（softmax值）
• 其次，最重点的，就是和X的相乘后的累加，到底是怎么对应相乘，怎么累加的，最终输出的梯度是什么形状【梯度和W的形状一样，对应的梯度计算及累加的对应元素大致如下。。。缭乱，但位置鲜明】
• 【望我日后回看，还能记得我现在脑子是怎么想的，并且希望日后会看，不会发现计算有问题。。。】

from sklearn import linear_model
import pandas as pd
import numpy as np

# 获取所需数据：'推荐分值', '推荐类型'
datas = pd.read_excel('./datas1.xlsx')
important_features = ['推荐分值', '推荐类型']
datas_1 = datas[important_features]


# 明确实际类别Y为'推荐类型'，X为'推荐分值'
Y_original = datas_1['推荐类型']
Y = np.expand_dims(Y_original, axis=1)
Y_0 = np.where(Y=='低推荐',1,0)
Y_1 = np.where(Y=='中推荐',1,0)
Y_2 = np.where(Y=='高推荐',1,0)
Y = np.concatenate((Y_0,Y_1,Y_2),axis=1)
X_original = datas_1.drop('推荐类型',axis=1)
X_original = (X_original-X_original.min())/(X_original.max()-X_original.min())
rows,columns = X_original.shape
class_nums = 3
X_0 = np.ones((rows,1))
X = np.concatenate((X_0,X_original),axis=1)

# Softmax函数的矩阵运算
def E_func(x):
    E_0 = np.exp(x)
    E_sum = np.sum(E_0,axis=1)
    E_sum = np.expand_dims(E_sum, axis=1)
    E_all = np.concatenate((E_sum,E_sum,E_sum),axis=1)
    E = E_0/E_all
    return E
# 手动softmax模型
def mul_log_inhand():
    W0 = np.zeros((class_nums, columns+1))
    Z_hat = np.matmul(X, W0.T)
    Y_hat = E_func(Z_hat)
    Loss0 = -np.sum(Y * Y_hat)
    a = 0.0005  # 设置学习率a
    times = 10000000
    num = 0
    while num <= times:
        # 损失函数求导：重难点！！！！困扰了半天！！！
        """重点，难点，值得哭泣的点！！！""
        gradient = []
        A = Y*(Y_hat-1)
        for i in range(A.shape[1]):
            temp = []
            for j in range(X.shape[1]):
                suu = np.sum(X[:,j]*A[:,i])
                temp.append(suu)
            gradient.append(temp)
        gradient = np.array(gradient)

        # 参数 W 迭代
        W1 = W0 - a * gradient

        # 迭代后重新计算 Loss 值，并判断迭代条件 Loss1 > Loss0
        Z_hat = np.matmul(X, W1.T)
        Y_hat = E_func(Z_hat)
        Loss1 = -np.sum(Y * Y_hat)
        if Loss1 > Loss0:
            break
        num += 1
        Loss0 = Loss1
        W0 = W1

    # 停止迭代后，输出模型参数
    print("——————————手动：梯度下降法——————————")
    print(f'模型参数W为：{W0}')

    # 计算sofgmax模型的预测概率结果
    Z_hat = np.matmul(X, W0.T)
    Y_hat = E_func(Z_hat)

    # 独热编码逆解过程：先计算最大概率的下标，根据下标不同，逆解为对应的标签（0-低推荐、1-中推荐、2-高推荐）
    Y_hat =list(np.argmax(Y_hat,axis=1))
    Y_hat = ["低推荐" if i==0 else i for i in Y_hat]
    Y_hat = ["中推荐" if i == 1 else i for i in Y_hat]
    Y_hat = ["高推荐" if i == 2 else i for i in Y_hat]

    # 输出分类结果及模型准确率等
    print("Y预测:",Y_hat)
    print(f"最终迭代次数为{num + 1}，损失值为{round(Loss0, 2)}")
    accurency = np.array([1 if Y_hat[i] == Y_original[i] else 0 for i in range(rows)])
    accurrency = round((np.sum(accurency)/rows*100),0)
    print(f"预测准确率：{accurrency}%")


# sklearn的梯度下降分类器
def mul_log():
    # 1. 建立模型：随机梯度下降分类模型
    classifier = linear_model.SGDClassifier(loss="log",penalty=None)

    # 2. 学习模型
    classifier.fit(X_original,Y_original)
    Y_predict = classifier.predict(X_original) # 模型分类
    labels = classifier.classes_ # 获取分类标签
    w = classifier.coef_ # 获取参数 W
    b = classifier.intercept_ # 获取偏差b，或称W0
    print("——————————sklearn：——————————")
    print(f'模型参数W为：{w}')

    # 3. 衡量模型
    accurency = classifier.score(X_original,Y_predict)
    print(f"预测准确率：{accurency*100}%")

mul_log_inhand()
mul_log()

虽然，我手动分类出来的准确率，是不够高，但这不重要 一点儿都不重要，it doesn’t matter

至少能够迭代分类啊，重点是能基础性地理解softmax的交叉熵函数求导过程