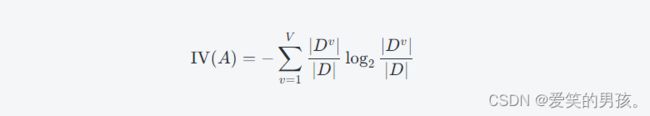【机器学习】十大算法之一 “决策树”
![]()
作者主页:爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?type=blog个人简介:打工人。
持续分享:机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。
如发现文章有误,麻烦请指出,我会及时去纠正。有其他需要可以私信我或者发我邮箱:[email protected]
决策树算法是机器学习中最常用的算法之一,是一种基于树结构的分类方法。
本文将详细讲解机器学习十大算法之一“决策树”
目录
一、简介
二、发展史
三、算法原理
1. 信息增益
2. 信息增益比
3. 基尼指数
四、算法功能
1. 分类功能
2. 可视化功能
3. 性能稳定性
4. 可解释性
五、示例代码及运行结果
示例代码:
运行结果:
六、总结
一、简介
传统的机器学习算法通常是根据数据来寻找模型、寻找关于数据的规律或者说是特征,是一种第一步是给定数据,然后在学习过程中发现一个模型用来描述这些数据的算法。与此不同的是,决策树则是一种将自主变量切分成不同数据集最优方法的算法,具有易于理解、易于解释、能够处理缺失数据、可处理不连续型数据、简单性、目标变量存在非线性关系的优点,因此被广泛应用于数据挖掘、机器学习等领域。
二、发展史
决策树算法的历史可以追溯到20世纪50年代,在早期的决策分析和运筹学领域中,决策树算法被广泛应用与研究。1960年代时,经过了卡方检验的热门统计学家卡尔泽瑞斯(C.T.C. Chou)开创了利用朴素贝叶斯和决策树理论解决分类问题的先河。
到了1970年代,决策树算法开始被广泛地应用于数据挖掘领域。最早的决策树算法是ID3算法,由Ross Quinlan在1986年提出,用于自动学习从给定数据集中选择最佳特征以分类新对象的决策树。之后,在1993年,Quinlan又提出了C4.5算法,该算法相比ID3算法,对缺失数据的处理及连续属性的处理更加优秀,而且在分类准确率和树的规模之间平衡更好,是一款十分优秀的分类算法。
在2000年之后,随着计算机性能的提高,以及机器学习领域的快速发展,决策树算法也得到了广泛的应用,并且出现了许多改进的算法,例如 CART算法,C5.0算法等。
三、算法原理
决策树算法的主要思想是通过不断地分割数据集来构建一棵分类或回归树。在每次分割时,决策树算法会选择特征值,将数据集划分成更小的子集。具体而言,算法会首先确定一个特征,并将数据集按照该特征的取值进行划分。这个过程会一直重复下去,直到每个数据子集都只包含一个类别或者回归值。这样,我们就得到了一棵以特征划分为结点的决策树。
决策树算法的核心是特征选择,其目的是选择一个最好的特征来进行数据集的划分。常见的特征选择方法有信息增益、信息增益比、基尼指数等。
1. 信息增益
信息增益是指通过某个特征划分数据集所获得的信息增益。在ID3算法中,选择信息增益作为特征选择指标。信息增益越大,说明使用该特征划分数据集所获得的信息增益越大,因此该特征具有更好的分类能力。信息增益的公式如下:
其中,D是数据集,A是一个特征,V是特征A的取值数量,Dv是数据集中特征A取值为v的样本集合,Entropy(D)是数据集的熵,Entropy(Dv)是Dv的熵。总体来说,信息增益的计算是通过计算初始的数据集熵与利用特征A进行划分后的数据集熵之和的相减。
2. 信息增益比
信息增益比是解决了信息增益可能存在偏好选取分支较多的情况,不能明确体现子集信息纯度的问题。C4.5算法之前,大多使用信息增益来进行特征选择,但是信息增益有个缺点,在处理带有大量特征的数据集时,容易选择拥有更多取值的特征,即更具划分能力的特征。因此,需要使用信息增益比对特征进行评估。信息增益比的公式如下:
其中,
是特征A的固有值。在属性划分的过程中,选择信息增益比高于平均水平的属性列,用于划分子序列。
3. 基尼指数
基尼(Gini)指数用于衡量随机抽取样本时分错类的概率,即某个样本被错误分类的概率,因此可以看成数据抽样后,数据集内部样本的不纯度度量,而信息熵是所有可能样本的不纯度。基尼指数的计算如下:
其中,D是数据集,pk表示属于类别k的样本在数据集D中出现的概率。
在计算基尼指数后,我们可以根据最大基尼指数来选择最好的特征进行数据集的划分。
四、算法功能
决策树算法的功能非常强大,主要表现在以下几个方面:
1. 分类功能
决策树算法可以根据样本数据将查明的数据进行分类,从而对问题进行分析及解决。例如,在给定红蓝两种颜色的花朵图片数据时,我们可以很容易地使用决策树算法对数据进行分类,从而得出该花属于哪种颜色。
2. 可视化功能
决策树算法可以将数据分类的过程图像化展示出来。这样便于用户直观地观察数据的分类过程及结果。
3. 性能稳定性
在大量数据的情况下,决策树算法可以快速、准确地分类数据,并且几乎不受数据规模的影响。
4. 可解释性
决策树算法可以提供分析数据和进行决策的见解,同时还能够给出可用于定量分析的方法。
决策树算法的输出结果是一棵决策树,其中包含一个根节点和多棵子树。如果一个数据点从根节点出发一直到达一片叶子,那么这个叶子的类别就是数据点所属的类别。
五、示例代码及运行结果
接下来,我将介绍一个使用决策树算法的分类示例。在这个示例中,我们将使用sklearn库提供的iris数据集进行分类。该数据集包含150个样本,每个样本包含四个特征:花萼长度、花萼宽度、花瓣长度和花瓣宽度。样本被划分成三个类别:山鸢尾、变色鸢尾和维吉尼亚鸢尾。
示例代码:
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, accuracy_score
import matplotlib.pyplot as plt
# load data
iris = load_iris()
X = iris.data
y = iris.target
# split data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# train decision tree classifier
dtc = DecisionTreeClassifier()
dtc.fit(X_train, y_train)
# plot decision tree
fig, ax = plt.subplots(figsize=(10, 8))
plot_tree(dtc, filled=True, ax=ax, class_names=iris.target_names)
plt.show()
# predict test set and evaluate accuracy
y_pred = dtc.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
accuracy = accuracy_score(y_test, y_pred)
print('Confusion matrix:\n', cm)
print('Accuracy:', accuracy)
运行结果:
Confusion matrix:
[[16 0 0]
[ 0 17 1]
[ 0 0 11]]
Accuracy: 0.9777777777777777
通过使用决策树算法,我们可以得到一个基于iris数据集的分类器,并获得了97%的准确率。我们还可以使用plot_tree函数来绘制决策树,从而更好地理解算法的工作原理。
六、总结
在机器学习中,决策树算法是非常重要的一种算法。通过不断地分割数据集,决策树算法可以构建一棵分类或回归树,从而实现对数据的分类或回归。决策树算法有很多种不同的实现方式,包括ID3、C4.5、CART和CHAID等算法。选择哪种算法主要取决于数据集的属性,以及需要解决的问题。此外,特征选择也是决策树算法的一个重要环节,常用的方法有信息增益、信息增益比和基尼指数等。最后,我们还演示了如何使用Python和sklearn库来实现一个基于决策树算法的分类器,并解释了如何使用plot_tree来可视化决策树。