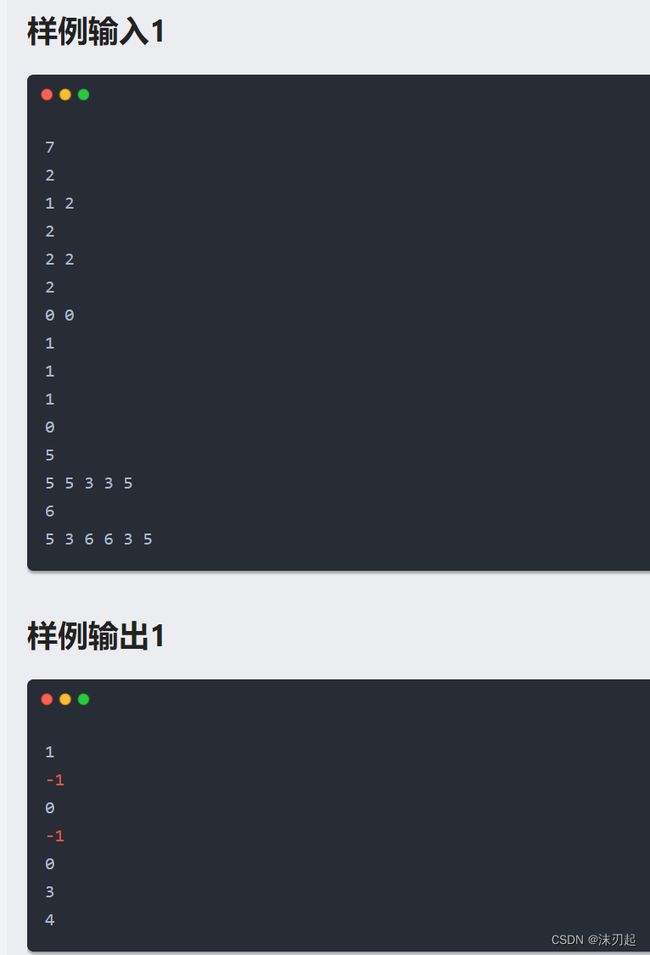
ahut 月赛1
心得:一点一点理解,对于一段要学习的代码,跟着写下来,理解一点写一点对于一道题目,用记事本,看题目,看一句题目,用自己的话概括一句,写在记事本上,并将自己的想法一并写下来这样做下来,心会很平静,你会发现,理解一段代码并不费力,解决一道题目并不费力,一切都成了顺理成章的事情
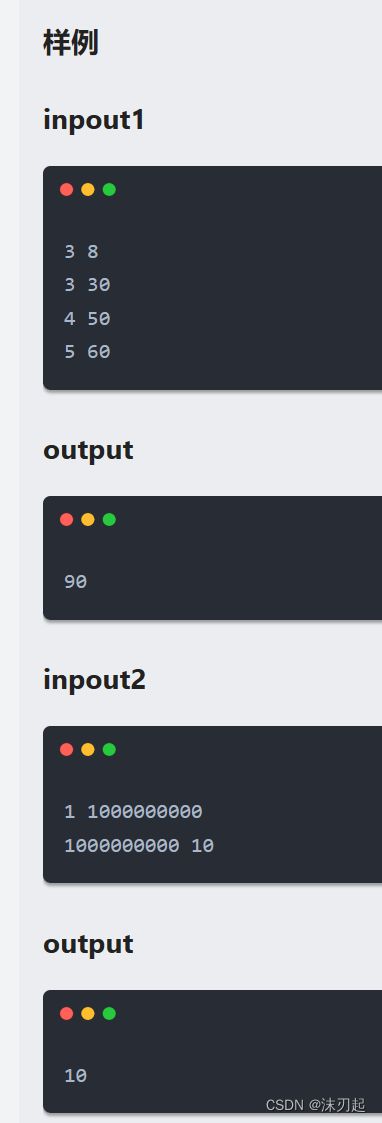
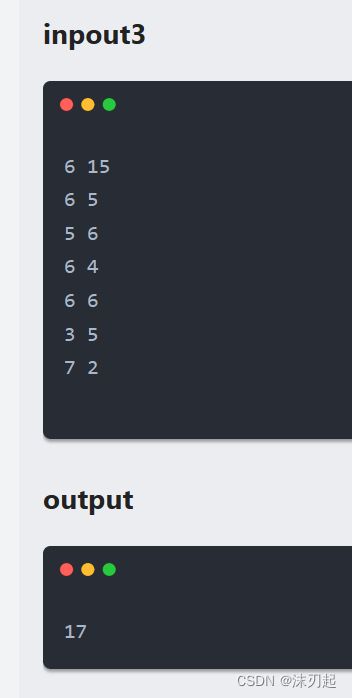
这题很明显就是01背包,但是问题在于背包容量m非常的大,高达1e9,这样的话肯定会爆空间
但是我们可以发现价值vi范围在1e3,然后物品最多100个,也就是价值v总和最多1e5
经典的01背包f[i][j]表示在前i个物品里选,容量为j所能放的物品最大总价值
我们可以用f[i][j]表示在前i个物品里选,价值为j所需要的物品最小总重量,这样的话,我们需要的空间为f[110][100010],不会爆空间
对于f[n][0到1e5],即在前n个物品里选,对于价值为0到1e5所需的最小总重量如果小于m的话,那么该价值就是合法的,然后在众多合法的价值里取最大就行了
注意,由于f的值是重量,求重量是取最小,所以一开始先要将f初始化为0x3f3f3f3f(经典的01背包是取最大,而f放在外部变量的位置,默认为0,就不需要初始化了),同时初始化f[0][0]为0
AC代码:
#include
#include
#include
#define int long long
using namespace std;
const int N=110,M=1e5+10;
int w[N];//重量
int v[N];//权值
int f[N][M];//f[i][j]==>第一维表示在前i个物品中选,第二维表示价值为j,f[i][j]的值表示最小重量
signed main()
{
memset(f,0x3f,sizeof f);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i]>>v[i];
f[0][0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=1e5;j++){
f[i][j]=f[i-1][j];
if(j-v[i]>=0) f[i][j]=min(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
int res=0;
for(int j=0;j<=1e5;j++){
if(f[n][j]<=m) res=max(res,j);
}
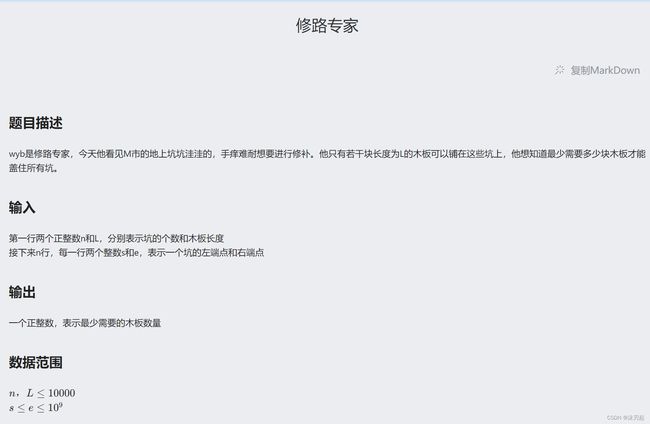
cout< B.修路专家
AhutOj
将所有区间按左端点从左到右排序,然后从左到右无缝隙补缺
#include
#include
#include
using namespace std;
const int N=1e4+10;
struct node{
int l,r;
bool operator<(const node &W)const{
return l>n>>l;
for(int i=1;i<=n;i++) cin>>q[i].l>>q[i].r;
sort(q+1,q+1+n);
int res=0;
int r=0;
for(int i=1;i<=n;i++){
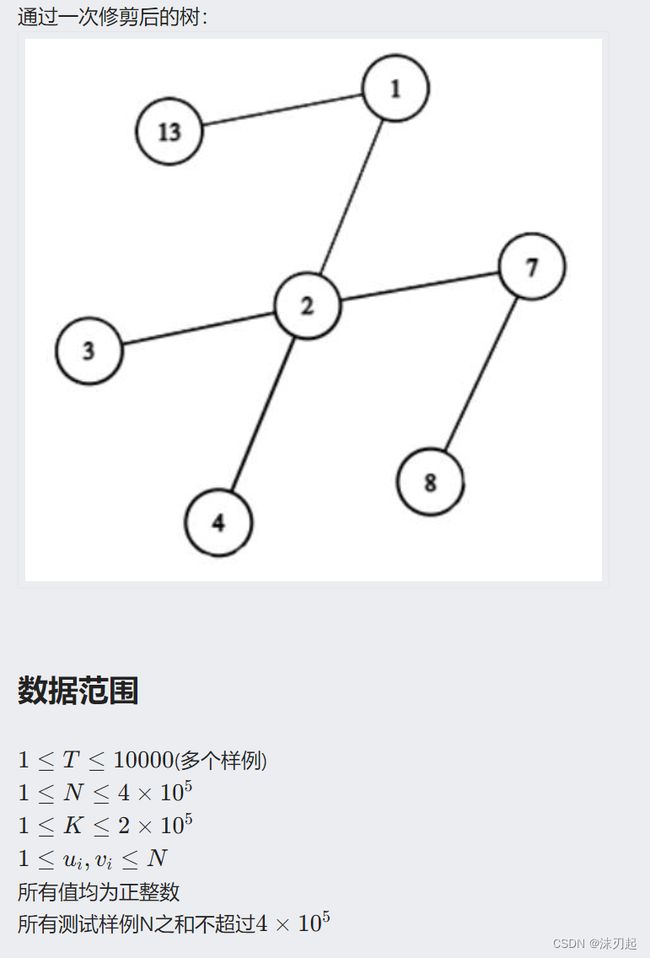
if(r C.小小园艺师
AhutOj
AC代码:
#include
#include
#include
#include
#include
#define int long long
using namespace std;
const int N=4e5+10;
int d[N];//统计度数
//换一种写法,写一个solve函数,我看好多大佬都这么写
void solve()
{
memset(d,0,sizeof d);//t组样例,每组样例都要初始化度数d
int n,k;
cin>>n>>k;
//先处理特殊情况,即只有一个点的情况,特殊情况优先考虑
if(n==1){
if(k>0) cout<<0< > e(n+1);//t组样例,用于建图,将点与点联系起来
for(int i=0;i>u>>v;
//点u和点v之间建立无向边
e[u].push_back(v);
e[v].push_back(u);
d[u]++;//点u的入度+1
d[v]++;//点v的入度+1
}
queueq;
for(int i=1;i<=n;i++){
if(d[i]==1) q.push(i);//遍历n个点,先将叶子节点(度数为1的点)入队
}
int res=n;//res表示节点的个数,初始为n
//一共k次操作,每次将叶子节点删去
while(k--){
if(!q.size()) break;//队列q里装的是叶子节点,当叶子节点都删完之后,表示本次操作结束了,就退出循环,准备下一次操作
queuep;//再定义一个队列p
while(q.size()){
int t=q.front();//在叶子节点的集合中取出队头
q.pop();//删除队头,我们的操作就是删除叶子节点
res--;//节点数减1
//把这个叶子节点删去后,相应地,与它相连的边要删除,与它相连的点的度数要减-1
//枚举和这个叶子节点相连的点
for(int i=0;i>t;
while(t--){
solve();
}
return 0;
} 可以用ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);来关闭输入输出同步
这样的话就可以t组数据全部输入好之后再一起全部输出
另外,换行用'\n'而不用endl,才可以做到不是输入一组输出一个答案
AC代码:
#include
#include
#include
#include
#include
#define iosy ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define int long long
#define endl '\n'
using namespace std;
const int N=4e5+10;
int d[N];//统计度数
//换一种写法,写一个solve函数,我看好多大佬都这么写
void solve()
{
memset(d,0,sizeof d);//t组样例,每组样例都要初始化度数d
int n,k;
cin>>n>>k;
//先处理特殊情况,即只有一个点的情况,特殊情况优先考虑
if(n==1){
if(k>0) cout<<0< > e(n+1);//t组样例,用于建图,将点与点联系起来
for(int i=0;i>u>>v;
//点u和点v之间建立无向边
e[u].push_back(v);
e[v].push_back(u);
d[u]++;//点u的入度+1
d[v]++;//点v的入度+1
}
queueq;
for(int i=1;i<=n;i++){
if(d[i]==1) q.push(i);//遍历n个点,先将叶子节点(度数为1的点)入队
}
int res=n;//res表示节点的个数,初始为n
//一共k次操作,每次将叶子节点删去
while(k--){
if(!q.size()) break;//队列q里装的是叶子节点,当叶子节点都删完之后,表示本次操作结束了,就退出循环,准备下一次操作
queuep;//再定义一个队列p
while(q.size()){
int t=q.front();//在叶子节点的集合中取出队头
q.pop();//删除队头,我们的操作就是删除叶子节点
res--;//节点数减1
//把这个叶子节点删去后,相应地,与它相连的边要删除,与它相连的点的度数要减-1
//枚举和这个叶子节点相连的点
for(int i=0;i>t;
while(t--){
solve();
}
return 0;
} D.跳格子
AhutOj
只有两种情况,如果n不是k的整数倍,那么就直接1步,直接到n
如果n是k的整数倍,那么就两步n-k-1和k+1
AC代码:
#include
#include
#include
using namespace std;
int main()
{
int t;
cin>>t;
while(t--){
int n,k;
cin>>n>>k;
if(n%k!=0){
cout<<1< E.狼人杀但是逆天
AhutOj
先对n个数从小到大排序,然后依次遍历,判断每个人是人还是狼人,先假设他是人,那么res-1如果大于等于这个人所说的至少有几个狼人的话,那么可以认定他是人
否则,他就是狼人,则标记一下出现了狼人,并且退出
判定一下,如果存在狼人,并且所确定的狼人数量大于等于确定的狼人x所说的狼人最少的数量,那么该狼人也说的是真话,就矛盾了,就输出-1,否则输出所确定的狼人数量
该题是模拟题,可以深入研究一下模拟
当看到一段看不懂的代码时,可以在记事本上按照代码从头到尾模拟一遍,可以快速理解
当自己写的代码不正确时,可以依照样例,在记事本上模拟一遍,然后知道代码错误之处,不断修正代码
AC代码:
#include
#include
#include
using namespace std;
const int N=110;
int a[N];
int main()
{
int t;
int x;
cin>>t;
while(t--){
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+1+n);
int res=n;
bool flag=false;
for(int i=1;i<=n;i++){
x=i;
if(res-1>=a[i]) res--;
else {
flag=true;
break;
}
}
cout<=a[x]) cout<<-1< F.昊昊的难题(hard)
AhutOj
f[i]表示在前i个字符中选,最多有多少个不以字符p结尾的合法的子序列
p[i]表示在前i个字符中选,最多有多少个以字符p结尾的合法的子序列
当s[i]为字符p时
状态转移,两种情况,对于字符p选与不选
p[i]=(p[i-1]+p[i-1]+f[i-1]+1)%mod;
p[i]==>
p[i-1]表示不选字符p,即在前i-1个字符中以p结尾的合法子序列的个数
p[i-1]+f[i-1]+1表示选字符p,其中p[i-1]表示在前i-1个字符中以p结尾的合法子序列加上字符p组成的子序列的个数,f[i-1]表示在前i-1个字符中不以p结尾的合法子序列加上p组成的子序列的个数,1表示单独将s[i]作为子序列
f[i]=f[i-1]%mod;
f[i]就直接由f[i-1]转移过来,因为最后一个字符是p,在前i个字符中选不以p结尾的和在前i-1个字符中选不以p结尾的是一样的
当s[i]为字符f时
状态转移,两种情况,对于字符f选与不选
p[i]=p[i-1]%mod;
p[i]直接由p[i-1]转移过来,因为最后一个字符不是p,在前i个字符中选以p结尾的和在前i-1个字符中选以p结尾的是一样的
f[i]=(f[i-1]+f[i-1]+1)%mod;
f[i]==>
f[i-1]表示不选字符f,即在前i-1个字符中不以字符p结尾的合法的子序列的个数
f[i-1]表示选字符f,即在前i-1个字符中不以字符p结尾的合法子序列和字符f组成的子序列的个数
1表示单独将s[i]作为子序列
如果s[i]既不是字符p也不是字符f
比如说是字符a,状态转移,两种情况,对于字符a选与不选
p[i]=p[i-1]%mod;
p[i]直接由p[i-1]转移过来,因为最后一个字符不是p,在前i个字符中选以p结尾的和在前i-1个字符中选以p结尾的是一样的
f[i]=(f[i-1]+p[i-1]+f[i-1]+1)%mod;
f[i]==>
f[i-1]表示不选字符a,即在前i-1个字符中不以字符p结尾的合法子序列的个数
p[i-1]+f[i-1]表示选字符a,即在前i-1个字符中以p结尾的合法子序列加上字符a组成的子序列的个数以及在前i-1个字符中不以字符p结尾的合法子序列加上字符a组成的子序列的个数,1表示单独将s[i]作为子序列
AC代码:
#include
#include
#include
using namespace std;
const int N=1e5+10,mod=1e9+7;
int f[N];//f[i]表示在前i个字符中选,最多有多少个不以字符p结尾的合法的子序列
int p[N];//p[i]表示在前i个字符中选,最多有多少个以字符p结尾的合法的子序列
void solve()
{
string s;
cin>>s;
int n=s.size();
if(s[0]=='p') p[0]=1;
else f[0]=1;
for(int i=1;i G.昊昊的难题(easy)
AhutOj
将连续的pf的p位置记下来,然后在前面的到p以及f到后面这两种字符串里面选连续的子串,长度为x,则个数为1+2+...+x即为x*(x+1)/2
AC代码:
#include
#include
#include
#include
using namespace std;
const int N=1e5+10;
int a[N];
int cnt;
int main()
{
string s;
cin>>s;
for(int i=0;i H.同构
AhutOj
这题和atcoder beginner contest 300 B题一样,见Atcoder Beginner Contest 300_沫刃起的博客-CSDN博客
I.屠龙勇士
AhutOj
独角兽和龙战斗
一共有n次攻击,ai表示第i次攻击的时间,从攻击开始,每秒会对龙造成1点伤害,毒药效果不会叠加
龙一共有h点生命值,如果对龙造成至少h点伤害,就会杀死龙
求k的最小值满足对龙至少造成h点伤害
很明显,用二分答案
刚开始不知道为什么用在[1,1e9]是wa,在[1,1e18]就AC了,原因在于虽然数组a的范围在1e9,但是答案完全可以1e18
AC代码:
#include
#include
#include
#include
#include
#define int long long
using namespace std;
const int N=110;
int a[N];
int n,h;
bool check(int x){
int res=0;
for(int i=1;i<=n-1;i++){
res+=min(x,a[i+1]-a[i]);
if(res>=h) return true;
}
if(res+x>=h) return true;
return false;
}
signed main()
{
int t;
cin>>t;
while(t--){
cin>>n>>h;
for(int i=1;i<=n;i++) cin>>a[i];
int l=1,r=1e18;
while(l