算法提高之动态规划：树形dp

1、树的最长路径(树的直径)

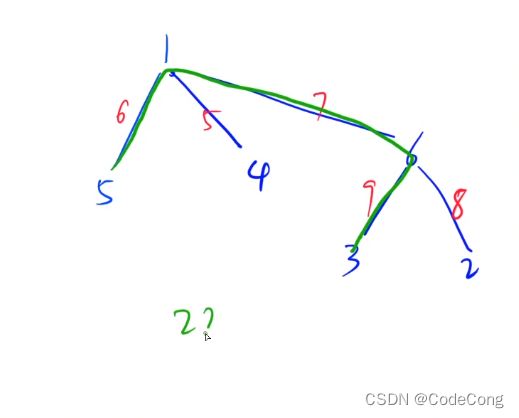
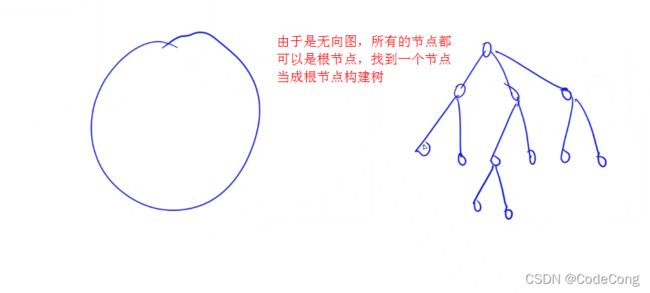
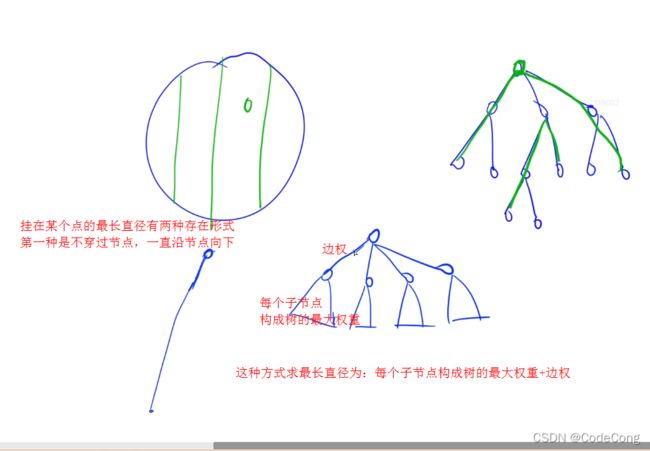
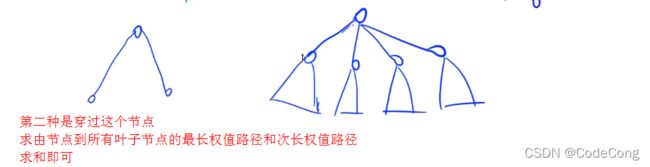
#include 
#include 
#include 

using namespace std;

const int N = 10010, M = N * 2, INF = 0x3f3f3f3f;

int n;
int h[N], e[M], w[M], ne[M], idx;
//d1表示向下走的最长路径  d2表示向下走的次长路径 up表示向上走的最长路径
//p1存储最大值和次大值是从哪个边上来的 需要判断父节点的最长边是不是从当前子树上来的
int d1[N], d2[N], p1[N], up[N];
//当某个节点是叶子节点的时候 记为true
bool is_leaf[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

//向下dfs 
int dfs_d(int u, int father)
{
    //求最长距离和次长距离，其中次长距离是为祥上深搜做准备的
    d1[u] = d2[u] = -INF;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        
        //dfs_d(1,7)  p1[1]=2;
        int d = dfs_d(j, u) + w[i];
        //对于父节点由很多个子节点，一个子节点对应一个d
        //d1[u] 是对父节点而言，所有子节点中最大的d
        //d2[u] 是对父节点而言，所有子节点中次大的d
        if (d >= d1[u])
        {
            d2[u] = d1[u], d1[u] = d;
            //u是父节点，j是子节点。对于父节点，最长距离是由哪个子节点产生的
            p1[u] = j;
        }
        else if (d > d2[u]) d2[u] = d;
    }
	//是一个叶子节点
    if (d1[u] == -INF)
    {
        d1[u] = d2[u] = 0;
        is_leaf[u] = true;
    }
	//返回最长路径的长度
    return d1[u];
}

//向上dfs

void dfs_u(int u, int father)
{
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        
        //1.dfs_u中处理向下走
        //p1[u]=j 记录的是再dfs_d中 
        //在父节点u处的最长路径是从j这个子节点过来的
		//因此在dfs_u中不能与dfs_d重复  则只能从次大值和up[u]更新
        if (p1[u] == j) up[j] = max(up[u], d2[u]) + w[i];
        else up[j] = max(up[u], d1[u]) + w[i];
        //2.dfs_u中处理向上走
        dfs_u(j, u);
    }
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    //将1号节点定义为根节点
	//向下走的最长距离和次长距离
    dfs_d(1, -1);
    //向上走的最长距离
    dfs_u(1, -1);
    
	//枚举每一个点
	//根节点向下走，叶子节点向上走。
    int res = d1[1];
    for (int i = 2; i <= n; i ++ )
        if (is_leaf[i]) res = min(res, up[i]);
        else res = min(res, max(d1[i], up[i]));

    printf("%d\n", res);

    return 0;
}

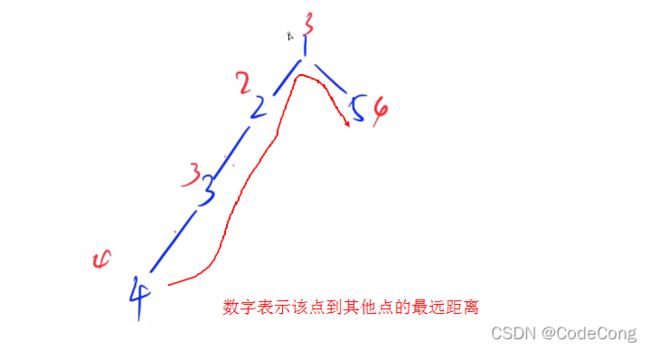
2、树的中心

#include 
#include 
#include 

using namespace std;

const int N = 10010, M = N * 2, INF = 0x3f3f3f3f;

int n;
int h[N], e[M], w[M], ne[M], idx;
//d1表示向下走的最长路径  d2表示向下走的次长路径 up表示向上走的最长路径
//p1存储最大值和次大值是从哪个边上来的 需要判断父节点的最长边是不是从当前子树上来的
int d1[N], d2[N], p1[N], up[N];
bool is_leaf[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dfs_d(int u, int father)
{
    d1[u] = d2[u] = -INF;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        int d = dfs_d(j, u) + w[i];
        if (d >= d1[u])
        {
            d2[u] = d1[u], d1[u] = d;
            p1[u] = j;
        }
        else if (d > d2[u]) d2[u] = d;
    }
	//是一个叶子节点
    if (d1[u] == -INF)
    {
        d1[u] = d2[u] = 0;
        is_leaf[u] = true;
    }
	//返回最长路径的长度
    return d1[u];
}

void dfs_u(int u, int father)
{
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
		//从u这个节点过来  只能从次大值更新
        if (p1[u] == j) up[j] = max(up[u], d2[u]) + w[i];
        else up[j] = max(up[u], d1[u]) + w[i];

        dfs_u(j, u);
    }
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
	//向下走的最长距离和次长距离
    dfs_d(1, -1);
    //xiang
    dfs_u(1, -1);
	//枚举每一个点
    int res = d1[1];
    for (int i = 2; i <= n; i ++ )
        if (is_leaf[i]) res = min(res, up[i]);
        else res = min(res, max(d1[i], up[i]));

    printf("%d\n", res);

    return 0;
}

3、数字转换(树的最长路径)

#include 
#include 
#include 

using namespace std;

const int N = 50010, M = N;

int n;
int h[N], e[M], w[M], ne[M], idx;
//存的是约数之和
int sum[N];
bool st[N];
int ans;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

int dfs(int u)
{
 
    int d1 = 0, d2 = 0;
    for (int i = h[u]; i!=-1; i = ne[i])
    {
       int j = e[i];
       int d = dfs(j)+1;
       if (d >= d1) d2 = d1, d1 = d;
       else if (d > d2) d2 = d;
       
    }

    ans = max(ans, d1 + d2);
    return d1;
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
	//i 约数
    for (int i = 1; i <= n; i ++ )
    	//写成j*i<=n 当j和i接近int的最大范围时，可能会溢出
    	//j倍数 j!=1是因为 x的约数之和不包含本身
        for (int j = 2; j <= n / i; j ++ )
            sum[i * j] += i;
	//判断约数之和是否小于数的本身  
	//i!=1 sum[i]=0 所有数字变换在不超过n的正整数范围内进行。正整数 
    for (int i = 2; i <= n; i ++ )
    	//如果是，以约数之和为父节点，约数为子节点，建立一条有向边    
        if (sum[i] < i)
        {
            add(sum[i], i);
            st[i]=true;
        }
	//有多棵树 只需要遍历树根（没有被标记过的就是树根）
    for (int i = 1; i <= n; i ++ )
        if (!st[i])
            dfs(i);

    cout << ans << endl;

    return 0;
}

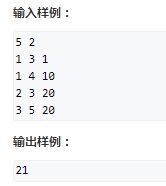
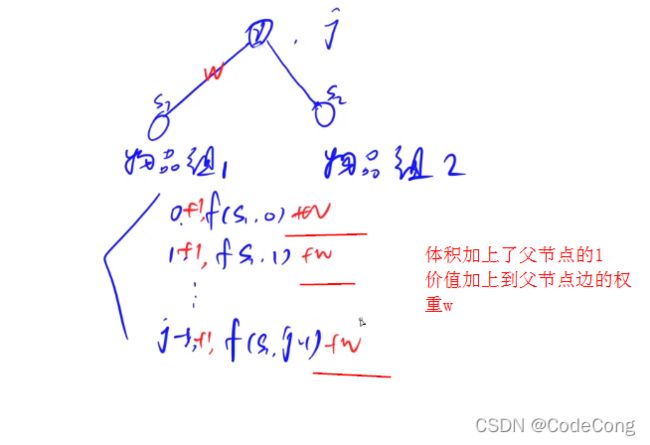
4、二叉苹果树(完全二叉树 有依赖的背包问题)

#include 
#include 
#include 

using namespace std;

const int N = 110, M = N * 2;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int f[N][N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u, int father)
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        if (e[i] == father) continue;
        dfs(e[i], u);
        //分组背包问题
        //e[i]物品组
        //体积 从大到小枚举
        //假设对于最后的叶子节点，依然按照m枚举，如果使用时超出m的范围
        //忽略不用即可
        for (int j = m; j>=0; j -- )
        	//决策 每一个子树的选择方式
            for (int k = 0; k + 1 <= j; k ++ )
            //f[u][j] 以u为根的子树中，选j条边的最大价值
                f[u][j] = max(f[u][j], f[u][j - k - 1] + f[e[i]][k] + w[i]);
    }
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    dfs(1, -1);
	//以1为根的子树中，选择m条边。剩余苹果的最大价值
    printf("%d\n", f[1][m]);

    return 0;
}

5、战略游戏

#include 
#include 
#include 

using namespace std;

const int N = 1510;

int n;
int h[N], e[N], ne[N], idx;
int f[N][2];
//判断父节点
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
//f[u][1] = 1 当前位置放上士兵就说明耗费1
//f[u][0]=0 是为了清空。多组测试数据 之前可能使用了f[u][0]
    f[u][0] = 0, f[u][1] = 1;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        f[u][0] += f[j][1];
        f[u][1] += min(f[j][0], f[j][1]);
    }
}

int main()
{
    while (cin >> n)
    {
    //多组测试数据  清空 头结点h  下标idx
        memset(h, -1, sizeof h);
        idx = 0;
	//清空父节点标记
        memset(st, 0, sizeof st);
        for (int i = 0; i < n; i ++ )
        {
            int id, cnt;
            scanf("%d:(%d)", &id, &cnt);
            while (cnt -- )
            {
                int ver;
                cin >> ver;
                add(id, ver);
                //ver有父节点
                st[ver] = true;
            }
        }

        int root = 0;
        while (st[root]) root ++ ;
        dfs(root);

        printf("%d\n", min(f[root][0], f[root][1]));
    }

    return 0;
}

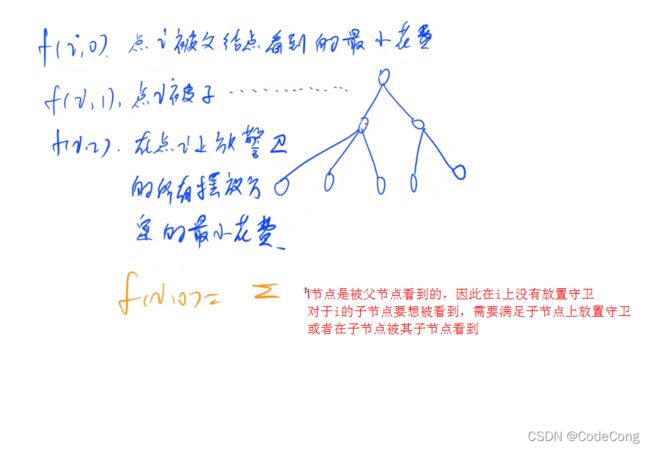
6、皇宫看守

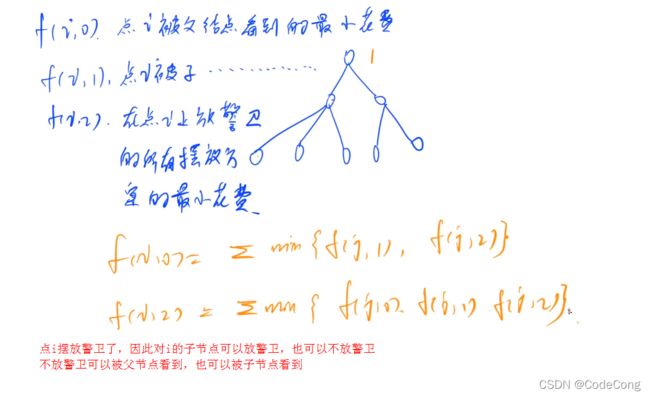
#include 
#include 
#include 

using namespace std;

const int N = 1510;

int n;
int h[N], w[N], e[N], ne[N], idx;
int f[N][3];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
    f[u][2] = w[u];
	//所有子节点f[j][1]和f[j][2]最小值的和
	//f[i][1]计算时需要除了被选的子节点之外的所有节点f[j][1]和f[j][2]的最小值之和
	//使用sum-k的就等于除k节点之外的其他节点f[j][1]和f[j][2]的最小值之和
    int sum = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        f[u][0] += min(f[j][1], f[j][2]);
        f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
        sum += min(f[j][1], f[j][2]);
    }

    f[u][1] = 1e9;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        f[u][1] = min(f[u][1], sum - min(f[j][1], f[j][2]) + f[j][2]);
    }
}

int main()
{
    cin >> n;

    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i ++ )
    {
        int id, cost, cnt;
        cin >> id >> cost >> cnt;
        w[id] = cost;
        while (cnt -- )
        {
            int ver;
            cin >> ver;
            add(id, ver);
            st[ver] = true;
        }
    }

    int root = 1;
    while (st[root]) root ++ ;

    dfs(root);
	//根节点被子节点看到，或者根节点上有守卫 根节点不可能有父节点
    cout << min(f[root][1], f[root][2]) << endl;

    return 0;
}

解释sum的用处

#include 
#include 
#include 

using namespace std;

const int N = 1510;

int n;
int h[N], w[N], e[N], ne[N], idx;
int f[N][3];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

//不写sum的写法
void dfs(int u)
{
    f[u][2] = w[u];
    
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        f[u][0] += min(f[j][1], f[j][2]);
        f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
       
    }

    f[u][1] = 1e9;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        f[u][1] = min(f[u][1], f[u][0] - min(f[j][1], f[j][2]) + f[j][2]);
    }
}

int main()
{
    cin >> n;

    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i ++ )
    {
        int id, cost, cnt;
        cin >> id >> cost >> cnt;
        w[id] = cost;
        while (cnt -- )
        {
            int ver;
            cin >> ver;
            add(id, ver);
            st[ver] = true;
        }
    }

    int root = 1;
    while (st[root]) root ++ ;

    dfs(root);

    cout << min(f[root][1], f[root][2]) << endl;

    return 0;
}