compressai的高斯建模GaussianCondition模块

超先验网络输出的$\sigma$和$\mu$，通过这两个参数对潜在表示y中的每一点都进行高斯建模，然后计算出每个像素值的概率，进行熵编码得到bit流。

理论

1、加入超先验网络的动机

以往的图像压缩都是对潜在表示整体进行熵建模，如假定整个潜在分布都服从同一分布，然而，当潜在表示存在统计依赖关系，这种全分解的熵模型并不能达到最优的压缩效果；
如果为潜在表示下的每个像素点分别估计各自的分布（均值和方差），在熵编码阶段中依据该信息，可以有效的消除原潜在表示中存在的边信息(Variational Image Compression with a Scale Hyperprior论文中的实验已经验证潜在分布y除以其方差确实可以减少相关性)

2、信息量及损失函数中bpp

信息量：表示该符号所需要的位数。

考虑用 0 和 1 组成的二进制数码为含有 n 个符号的某条消息编码，假设符号$a_j$在整条消息中重复出现的概率为 $P_j$ ，则该符号的信息量定义为：
$$E_n=-lo{g}_2(P_j)$$
信息量表示为以 2 为底的对数，是正值。

举例说明:

输入信源字符串：aabbaccbaa

a、b、c 出现的概率分别为 0.5、0.3 和 0.2，他们的信息量分别为：
$$\begin{gathered} E_a=-lo{g}_{2}0.5=1 \\ {E}_b=-lo{g}_{2}0.3=1.737 \\ {E}_c=-lo{g}_{2}0.2=2.322 \end{gathered}$$
总信息量也即表达整个字符串需要的位数：
$$E=E_a\times 5+E_b\times 3+E_c\times 2=14.855(bits)$$
a有5个，b有3个，c有2个，总bit数为14.855bit

熵编码的概念

3、误差函数

在数学中，误差函数（也称之为高斯误差函数，error function or Gauss error function）是一个非基本函数；

高斯函数的不定积分是误差函数。在统计学与机率论中，高斯函数是常态分布的密度函数，根据中心极限定理它是复杂总和的有限机率分布。正态函数从均值μ开始到指定值x的概率如下：

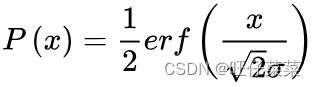
python代码中用的是torch.erfc()函数，但是你从头屡到尾就可以发现是等同的，只不过添加了很多正负号的提取转换之类的操作；

代码

GaussianCondition模块会返回两个值：量化后的值outputs、每个待编码值的出现概率的估计likelihood

主要讲likehood参数：

用处：

损失函数中需要likehood计算bpp，具体的代码数值对应的理论见上述理论2

注：代码不全，只提取助于理解部分

# train.py中调用RateDistortionLoss()函数
def train_one_epoch(
    model, criterion, train_dataloader, optimizer, aux_optimizer, epoch, clip_max_norm
):
    model.train()
    device = next(model.parameters()).device

    for i, d in enumerate(train_dataloader):
        d = d.to(device)

        optimizer.zero_grad()
        aux_optimizer.zero_grad()

        out_net = model(d)  # out_net包含两个量: "x_hat", "likelihoods"

        out_criterion = criterion(out_net, d)  # 之前定义的criterion = RateDistortionLoss(lmbda=args.lmbda)
        out_criterion["loss"].backward()
        if clip_max_norm > 0:
            torch.nn.utils.clip_grad_norm_(model.parameters(), clip_max_norm)
        optimizer.step()

        aux_loss = model.aux_loss()
        aux_loss.backward()
        aux_optimizer.step()
       
    
# rate_distortion.py中RateDistortionLoss()函数
@register_criterion("RateDistortionLoss")
class RateDistortionLoss(nn.Module):
    
    def forward(self, output, target):
        N, _, H, W = target.size()
        out = {}
        num_pixels = N * H * W

        # bpp
        out["bpp_loss"] = sum(
            (torch.log(likelihoods).sum() / (-math.log(2) * num_pixels))
            for likelihoods in output["likelihoods"].values()
        )

如何计算likehood：

class GaussianConditional(EntropyModel):
    
    def _standardized_cumulative(self, inputs: Tensor) -> Tensor:
        half = float(0.5)
        const = float(-(2**-0.5))
        # Using the complementary error function maximizes numerical precision.
        return half * torch.erfc(const * inputs)
    
    def _likelihood(
        self, inputs: Tensor, scales: Tensor, means: Optional[Tensor] = None
    ) -> Tensor:
        half = float(0.5)

        if means is not None:
            values = inputs - means
        else:
            values = inputs

        scales = self.lower_bound_scale(scales)  # σ下界，防止梯度消失

        # 使用erfc函数计算出高斯模型中潜在表示y中每个点的概率
        values = torch.abs(values)
        upper = self._standardized_cumulative((half - values) / scales)  
        lower = self._standardized_cumulative((-half - values) / scales)
        likelihood = upper - lower
        
    def forward(
        self,
        inputs: Tensor,
        scales: Tensor,
        means: Optional[Tensor] = None,
        training: Optional[bool] = None,
    ) -> Tuple[Tensor, Tensor]:
        if training is None:
            training = self.training
        outputs = self.quantize(inputs, "noise" if training else "dequantize", means)  # outputs返回量化参数
        likelihood = self._likelihood(outputs, scales, means)  # 每个待编码值出现的概率估计
        if self.use_likelihood_bound:
            likelihood = self.likelihood_lower_bound(likelihood)
        return outputs, likelihood