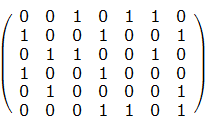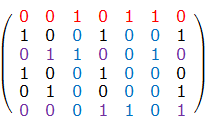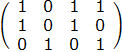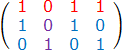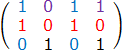dancing links x（舞蹈链算法）详解

dancing links x 详解 大佬万仓一黍的blog

夜深人静写算法（九）- Dancing Links X（跳舞链）

精确覆盖问题的定义：给定一个由0-1组成的矩阵，是否能找到一个行的集合，使得集合中每一列都恰好包含一个1

如下图，表示的是一个6×7的01矩阵。我们可以通过选择第1、5、6行使得这些行集合中每列恰有一个“1”（“恰有”的意思是有且仅有）。

1、穷举法
穷举的意思就是枚举所有状态，每一行的状态有“选”和“不选”两种，那么R行的状态数就是2^R。所以穷举的复杂度是指数级的。穷举的常用实现就是深度优先搜索：对于一个R×C的矩阵，枚举每一行r的“选”与“不选”，第r行“选”的条件是它和已经选择的行集合都没有冲突（两行冲突的定义是两行中至少存在一列上的两个数字均为“1”）。当已经选择的行集合中所有的列都恰有一个“1”时算法终止。
那么，枚举每行选与不选的时间复杂度为O(2^R)，每次选行时需要进行冲突判定，需要遍历之前选择的行集合的所有列，冲突判定的最坏时间复杂度为O(RC)，所以整个算法的最坏复杂度O(RC* 2^R)。
这里可以加入一个很明显的优化：由于问题的特殊性，即选中的行集合的每列只能有一个“1”。所以可以利用一个全局的哈希数组H[]标记当前状态下列的选择情况（H[c]=1表示第c列已经有一个“1”了）。这样每次进行冲突判定的时候就不需要遍历之前所有的行，而只需要遍历这个哈希数组H，遍历的最坏复杂度为O©。选中一个没有冲突的行之后，用该行里有“1”的列去更新哈希数组H，复杂度也是O©（需要注意的是：深搜在回溯的时候，需要将哈希数组标记回来）。所以整个算法的最坏复杂度为O(C*2^R)。 对于R和C都在15以内的情况，时间复杂度的数量级大概在 10 ^ 6，已经可以接受了。
【例题1】 给定一个R×C（R <= 20, C <= 50）的01矩阵，问是否存在这样一个行集合，使得集合中每一列恰有一个“1”。
这题和上一题的区别在于R和C的数据量，总数据规模是之前的四倍多，观察数据量，如果利用穷举+哈希，那么时间复杂度是10^8的数量级，已经无法满足我们的需求。这时可以采用状态压缩。

2、状态压缩
状态压缩一般用在动态规划中，这里我们可以将它进行扩展，运用到搜索里。
考虑上述矩阵的某一行，这一行中的每个元素的值域是[0, 1]，所以可以把每个元素想象成二进制数字的某一位，那么我们可以将一个二维矩阵的每一行压缩成一个二进制数，使得一个二维矩阵变成一个一维数组（降维）。

由于列数C的上限是50，所以可以把每一行用一个64位的整型来表示。
然后我们可以把问题的求解相应做一个转化，变成了求一个一维数组的子集，子集中的数满足两个条件：
(1) 任意两个数的“位与”(C++中的’&’)等于0;
(2) 所有数的“位或”(C++的’|’)等于2^C - 1;
第1)条很容易理解，倘若存在某两个数的“位与”不等于0，那么在这两个数的二进制表示中势必存在某一位都为1，即一列上至少有两个“1”，不满足题目要求；第2)条可以这么理解，所有数的“位或”等于2^C - 1，代表选出的数中所有位都至少有一个“1”，结合第1)条，代表选出的数中所有位至多有一个“1”。与之前的矩阵精确覆盖问题等价转化。
那么我们依旧采用穷举法，枚举每个数的“选”与“不选”。需要用到一个64位整型的辅助标记X（相对于之前的哈希数组H），X表示所有已经选择数的“位或”和。那么第r个数“选”的话则需要满足它和X的“位与”等于0（这个简单的操作相当于之前提到的行冲突判定）。辅助标记X的判定和更新的时间复杂度都是O(1)的，所以总的时间复杂度就是穷举的复杂度，即O(2^R)。

【例题2】 给定一个R×C（R <= 50, C <= 200）的01矩阵，问是否存在这样一个行集合，使得集合中每一列恰有一个“1”。
数据量进一步扩大，我们发现单纯的穷举已经完全没法满足需求，需要对算法进行进一步改进。那我们的主角 dancing links x（舞gaisuan蹈链算法） 就登场了，该算法就是 dfs 结合 十字交叉双循环链表。

3、回溯法
还是采用枚举的思想，不同的是这次的枚举相对较智能化。具体思路是当枚举某一行的时候，预先把和这行冲突的行、列都从矩阵中删除，这样一来避免下次枚举到无用的行，大大减少搜索的状态空间。

基本思路：
例如：如下的矩阵

就包含了这样一个集合（第1、4、5行）

如何利用给定的矩阵求出相应的行的集合呢？我们采用回溯法

矩阵1：

先假定选择第1行，如下所示：

如上图中所示，红色的那行是选中的一行，这一行中有3个1，分别是第3、5、6列。

由于这3列已经包含了1，故，把这三列往下标示，图中的蓝色部分。蓝色部分包含3个1，分别在2行中，把这2行用紫色标示出来

根据定义，同一列的1只能有1个，故紫色的两行，和红色的一行的1相冲突。

那么在接下来的求解中，红色的部分、蓝色的部分、紫色的部分都不能用了，把这些部分都删除，得到一个新的矩阵

矩阵2：

行分别对应矩阵1中的第2、4、5行

列分别对应矩阵1中的第1、2、4、7列

于是问题就转换为一个规模小点的精确覆盖问题

在新的矩阵中再选择第1行，如下图所示

还是按照之前的步骤，进行标示。红色、蓝色和紫色的部分又全都删除，导致新的空矩阵产生，而红色的一行中有0（有0就说明这一列没有1覆盖）。说明，第1行选择是错误的

那么回到之前，选择第2行，如下图所示

按照之前的步骤，进行标示。把红色、蓝色、紫色部分删除后，得到新的矩阵

矩阵3：

行对应矩阵2中的第3行，矩阵1中的第5行

列对应矩阵2中的第2、4列，矩阵1中的第2、7列

由于剩下的矩阵只有1行，且都是1，选择这一行，问题就解决

于是该问题的解就是矩阵1中第1行、矩阵2中的第2行、矩阵3中的第1行。也就是矩阵1中的第1、4、5行

在求解这个问题的过程中，我们第1步选择第1行是正确的，但是不是每个题目第1步选择都是正确的，如果选择第1行无法求解出结果出来，那么就要推倒之前的选择，从选择第2行开始，以此类推

从上面的求解过程来看，实际上求解过程可以如下表示

1、从矩阵中选择一行

2、根据定义，标示矩阵中其他行的元素

3、删除相关行和列的元素，得到新矩阵

4、如果新矩阵是空矩阵，并且之前的一行都是1，那么求解结束，跳转到6；新矩阵不是空矩阵，继续求解，跳转到1；新矩阵是空矩阵，之前的一行中有0，跳转到5

5、说明之前的选择有误，回溯到之前的一个矩阵，跳转到1；如果没有矩阵可以回溯，说明该问题无解，跳转到7

6、求解结束，把结果输出

7、求解结束，输出无解消息

从如上的求解流程来看，在求解的过程中有大量的缓存矩阵和回溯矩阵的过程。而如何缓存矩阵以及相关的数据（保证后面的回溯能正确恢复数据），也是一个比较头疼的问题（并不是无法解决）。以及在输出结果的时候，如何输出正确的结果（把每一步的选择转换为初始矩阵相应的行）。

于是算法大师Donald E.Knuth（《计算机程序设计艺术》的作者）出面解决了这个方面的难题。他提出了DLX（Dancing Links X）算法。实际上，他把上面求解的过程称为X算法，而他提出的舞蹈链（Dancing Links）实际上并不是一种算法，而是一种数据结构。一种非常巧妙的数据结构，他的数据结构在缓存和回溯的过程中效率惊人，不需要额外的空间，以及近乎线性的时间。而在整个求解过程中，指针在数据之间跳跃着，就像精巧设计的舞蹈一样，故Donald E.Knuth把它称为Dancing Links（中文译名舞蹈链）。

Dancing Links的核心是基于双向链的方便操作（移除、恢复加入）

我们用例子来说明

假设双向链的三个连续的元素，A1、A2、A3，每个元素有两个分量Left和Right，分别指向左边和右边的元素。由定义可知

A1.Right=A2，A2.Right=A3

A2.Left=A1，A3.Left=A2

在这个双向链中，可以由任一个元素得到其他两个元素，A1.Right.Right=A3，A3.Left.Left=A1等等

现在把A2这个元素从双向链中移除（不是删除）出去，那么执行下面的操作就可以了

A1.Right=A3，A3.Left=A1

那么就直接连接起A1和A3。A2从双向链中移除出去了。但仅仅是从双向链中移除了，A2这个实体还在，并没有删除。只是在双向链中遍历的话，遍历不到A2了。

那么A2这个实体中的两个分量Left和Right指向谁？由于实体还在，而且没有修改A2分量的操作，那么A2的两个分量指向没有发生变化，也就是在移除前的指向。即A2.Left=A1和A2.Right=A3

如果此时发现，需要把A2这个元素重新加入到双向链中的原来的位置，也就是A1和A3的中间。由于A2的两个分量没有发生变化，仍然指向A1和A3。那么只要修改A1的Right分量和A3的Left就行了。也就是下面的操作

A1.Right=A2，A3.Left=A2

仔细想想，上面两个操作（移除和恢复加入）对应了什么？是不是对应了之前的算法过程中的关键的两步？

移除操作对应着缓存数据、恢复加入操作对应着回溯数据。而美妙的是，这两个操作不再占用新的空间，时间上也是极快速的

在很多实际运用中，把双向链的首尾相连，构成循环双向链

Dancing Links用的数据结构是交叉十字循环双向链

而Dancing Links中的每个元素不仅是横向循环双向链中的一份子，又是纵向循环双向链的一份子。

因为精确覆盖问题的矩阵往往是稀疏矩阵（矩阵中，0的个数多于1），Dancing Links仅仅记录矩阵中值是1的元素。

Dancing Links中的每个元素有6个分量

分别：Left指向左边的元素、Right指向右边的元素、Up指向上边的元素、Down指向下边的元素、Col指向列标元素、Row指示当前元素所在的行

Dancing Links还要准备一些辅助元素（为什么需要这些辅助元素？没有太多的道理，大师认为这能解决问题，实际上是解决了问题）

Ans（）：Ans数组，在求解的过程中保留当前的答案，以供最后输出答案用。

Head元素：求解的辅助元素，在求解的过程中，当判断出Head.Right=Head（也可以是Head.Left=Head）时，求解结束，输出答案。Head元素只有两个分量有用。其余的分量对求解没啥用

C元素：辅助元素，称列标元素，每列有一个列标元素。本文开始的题目的列标元素分别是C1、C2、C3、C4、C5、C6、C7。每一列的元素的Col分量都指向所在列的列标元素。列标元素的Col分量指向自己（也可以是没有）。在初始化的状态下，Head.Right=C1、C1.Right=C2、……、C7.Right=Head、Head.Left=C7等等。列标元素的分量Row=0，表示是处在第0行。

简易版code：

#include
#include
#include
#include
#include
#include
using namespace std;
  
#define MAXM 1010
#define MAXN 1010
#define INF 0x3f3f3f3f
typedef long long int LL;
  
int L[MAXM*MAXN],R[MAXM*MAXN];
int D[MAXM*MAXN],U[MAXM*MAXN];
  
int S[MAXN]; //统计当前列中有多少个元素（即1的数量，以供dfs时查找最小值，减少搜索量）
int nRow[MAXM*MAXN],nCol[MAXN*MAXM];//当前元素所在行列的编号
  
int head;//这是整个图的表头
int ans[MAXM];//记录解
  
int M,N,Cnt;
bool finded;//已找到正确结果
 
void Del(int num) //删去num所在列中所有1的行（除了num本身）
{
    L[R[num]]=L[num];
    R[L[num]]=R[num];
	
    for(int i=D[num];i!=num;i=D[i]) //因为是环形，所以可以环游当前列的链表
        for(int j=R[i];j!=i;j=R[j]) //这里也可以环游当前行的链表
        {
            U[D[j]]=U[j];  //在元素所在列中删去当前元素
            D[U[j]]=D[j];
            --S[nCol[j]];   //列上元素数量减一
        }
}
  
void Resume(int num) //恢复num所在列中所有1的行（与删除原理相同，但需要反向）
{
    for(int i=U[num];i!=num;i=U[i])
        for(int j=L[i];j!=i;j=L[j])
		{
			U[D[j]]=D[U[j]]=j; //在元素所在列中插入（恢复）当前元素
			++S[nCol[j]];         //列上元素数量加一
		}
	
    L[R[num]]=R[L[num]]=num;
}
 
void dfs()
{   //printf("%d\n",ans[0]);
    if(R[head]==head)  //行链表中所有元素都已删除,找到可行解 
    {
        finded=1;
        return;
    }
	
    int Smin=INF,c=-1;    //找到1数量最少的边 
    for(int i=R[head];i!=head;i=R[i])
    {
        if(!S[i])      //剪枝，有s[i] = 0的列就没必要往下搜了
            return;
		
        if(S[i]<Smin)    //剪枝， 按s[i]从小到大的顺序遍历列
        {
            Smin=S[i];
            c=i;
        }
    }
	
    Del(c);
	
    //枚举当前列上的‘1’并选择 
    for(int i=D[c];i!=c;i=D[i])
    {
        ans[++ans[0]]=nRow[i];
		
        for(int j=R[i];j!=i;j=R[j])//删去所有与当前行中1矛盾的行
            Del(nCol[j]);
		
        dfs();
        if(finded) return;
		
        --ans[0];
        for(int j=L[i];j!=i;j=L[j])//恢复所有与当前行中1矛盾的行
            Resume(nCol[j]);
    }
	
    Resume(c); //还原现场
}
 
bool Init()
{
    ans[0] = head = finded = 0;
    L[head]=R[head]=U[head]=D[head]=head;
	
    if(~scanf("%d%d",&M,&N))
    {
        int i,j;
		
        for(i=0;i<=N;i++)
		{
			S[i]=0;
			L[i]=i-1;
			R[i]=i+1;
			U[i]=D[i]=i;
                        S[i]=0;
		}
		L[0]=N;
		R[N]=0;
		Cnt=N+1;
		
        for(i=1;i<=M;++i)
        {
            int a,b,begin,end;
            scanf("%d",&a);
			
			begin=end=Cnt;
            for(j=1;j<=a;++j)
            {
                scanf("%d",&b);
				S[b]++;
				nCol[Cnt]=b;
				nRow[Cnt]=i;
				
				//在列插入
				U[D[b]]=Cnt;
				D[Cnt]=D[b];
				U[Cnt]=b;
				D[b]=Cnt;
				
				//在行上插入
				L[Cnt]=end;
				R[end]=Cnt;
				R[Cnt]=begin;
				L[begin]=Cnt;
				end=Cnt;
				
				++Cnt;
            }
        }
		
        return 1;
    }
    else return 0;
}
  
void print()
{
    if(!finded)
    {
        puts("NO");
        return;
    }
	
    sort(ans+1,ans+ans[0]+1);
    printf("%d",ans[0]);
    for(int i=1;i<=ans[0];++i)
        printf(" %d",ans[i]);
    puts("");
}
  
int main()
{ 
    //freopen("in.txt","r",stdin);
    //freopen("out1.txt","w",stdout);
	
    while(Init())
    {
        dfs();
        print();
    }
}

工业级code：

  
/*
Dancing Links 高效搜索算法
   1) 如果矩阵A没有列（即空矩阵），则当前记录的解为一个可行解；算法终止，成功返回；
   2) 否则选择矩阵A中“1”的个数最少的列c；（确定性选择）
   3) a.如果存在A[r][c]=1的行r，将行r放入可行解列表，进入步骤4)；（非确定性选择）
      b.如果不存在A[r][c]=1的行r，则剩下的矩阵不可能完成精确覆盖，说明之前的选择有错（或者根本就无解），需要回溯，并且恢复此次删除的行和列，然后跳到步骤3)a；
   4)对于所有的满足A[r][j]=1的列j
        对于所有满足A[i][j]=1的行i，将行i从矩阵A中删除；
     将列j从矩阵A中删除；
   5) 在不断减少的矩阵A上递归重复调用上述算法；
   
Author: WhereIsHeroFrom
Update Time: 2018-3-21
Algorithm Complexity: NP
*/

#include 
#include 
#include 
#include 
using namespace std;

#define MAXR 510
#define MAXC 920
#define MAXB 62
#define MAXROWCODE ((MAXC+MAXB-1)/MAXB)
#define INF -1
#define INT64 long long

enum eCoverType {
	ECT_EXACT = 0,       // 精确覆盖
	ECT_REPEAT = 1,      // 重复覆盖
};

/*
DLXNode
	left, right        十字交叉双向循环链表的左右指针
	up, down           十字交叉双向循环链表的上下指针
	<用于列首结点>
	colSum             列的结点总数
	colIdx             列的编号
		
	<用于行首结点/元素结点>
	colHead            指向列首结点的指针
	rowIdx             DLXNode结点在原矩阵中的行标号
*/
class DLXNode {
public:
	DLXNode *left, *right, *up, *down;
	union {
		struct {
			DLXNode *colHead;   
			int rowIdx;
		}node;
		struct {
			int colIdx;
			int colSum;
		}col;
	}data;
public:
	//
	// 获取/设置 接口
	void resetCol(int colIdx);
	void resetColSum();
	void updateColSum(int delta);
	int getColSum();

	void setColIdx(int colIdx);
	int getColIdx();

	void setColHead(DLXNode *colPtr);
	DLXNode *getColHead();

	void setRowIdx(int rowIdx);
	int getRowIdx();

	///
	// 搜索求解用到的接口
	void appendToCol(DLXNode *colPtr);
	void appendToRow(DLXNode *rowPtr);

	void deleteFromCol();
	void resumeFromCol();

	void deleteFromRow();
	void resumeFromRow();
	///
};

void DLXNode::resetCol(int colIdx) {
	// IDA*的时候需要用到列下标进行hash
	setColIdx(colIdx);
	// 初始化每列结点个数皆为0
	resetColSum();
}
void DLXNode::resetColSum() {
	data.col.colSum = 0;
}

void DLXNode::updateColSum(int delta) {
	data.col.colSum += delta;
}

int DLXNode::getColSum() {
	return data.col.colSum;
}

void DLXNode::setColIdx(int colIdx) {
	data.col.colIdx = colIdx;
}
int DLXNode::getColIdx() {
	return data.col.colIdx;
}

void DLXNode::setColHead(DLXNode * colPtr) {
	data.node.colHead = colPtr;
}

DLXNode* DLXNode::getColHead() {
	return data.node.colHead;
}

void DLXNode::setRowIdx(int rowIdx) {
	data.node.rowIdx = rowIdx;
}

int DLXNode::getRowIdx() {
	return data.node.rowIdx;
}

void DLXNode::appendToCol(DLXNode * colPtr) {
	// 赋值列首指针
	setColHead(colPtr);

	// 这几句要求插入结点顺序保证列递增，否则会导致乱序（每次插在一列的最后）
	up = colPtr->up;
	down = colPtr;
	colPtr->up = colPtr->up->down = this;

	// 列元素++
	colPtr->updateColSum(1);
}

void DLXNode::appendToRow(DLXNode* rowPtr) {
	// 赋值行编号
	setRowIdx(rowPtr->getRowIdx());

	// 这几句要求插入结点顺序保证行递增（每次插在一行的最后）
	left =  rowPtr->left;
	right = rowPtr;
	rowPtr->left = rowPtr->left->right = this;
}

void DLXNode::deleteFromCol() {		
	left->right = right;
	right->left = left;
}

void DLXNode::resumeFromCol() {	
	right->left = left->right = this;
}

void DLXNode::deleteFromRow() {
	up->down = down;
	down->up = up;
	if (getColHead())
		getColHead()->updateColSum(-1);
}

void DLXNode::resumeFromRow() {
	if (getColHead())
		getColHead()->updateColSum(1);
	up->down = down->up = this;
}

/*
DLX （单例）
	head               head 只有左右（left、right）两个指针有效，指向列首
	rowCount, colCount 本次样例矩阵的规模（行列数）
	row[]              行首结点列表
	col[]              列首结点列表
	
	dlx_pool           结点对象池（配合dlx_pool_idx取对象）
*/
class DLX {
	DLXNode *head;             // 总表头
	int rowCount, colCount;    // 本次样例矩阵的规模（行列数） 
	DLXNode *row, *col;        // 行首结点列表 / 列首结点列表
	
	DLXNode *dlx_pool;         // 结点对象池
	int dlx_pool_idx;          // 结点对象池下标

	eCoverType eCType;
	int  *col_coverd;          // 标记第i列是否覆盖，避免重复覆盖
	INT64 *row_code;           // 每行采用二进制标记进行优化
	int limitColCount;         // 限制列的个数
							   // 即 前 limitColCount 列满足每列1个"1"，就算搜索结束
							   // 一般情况下 limitColCount == colCount 
public: 
	int *result, resultCount;  // 结果数组
	int minResultCount; 
	
private: 
	DLX() {
		dlx_pool_idx = 0;
		head = NULL;
		dlx_pool = new DLXNode[MAXR*MAXC];
		col = new DLXNode[MAXC+1];
		row = new DLXNode[MAXR];
		result = new int[MAXR];
		col_coverd = new int[MAXC+1];
		row_code = new INT64[MAXR*MAXROWCODE];
	}

	~DLX() {
		delete [] dlx_pool;
		delete [] col;
		delete [] row;
		delete [] result;
		delete [] col_coverd;
		delete [] row_code;
	}

	void reset_size(int r, int c, int limitC = INF, eCoverType ect = ECT_EXACT) {
		rowCount = r;
		colCount = c;
		limitColCount = limitC != INF? limitC : c; 
		eCType = ect;
		dlx_pool_idx = 0;
		resultCount = minResultCount = -1;
	}

	void reset_col();
	void reset_row();
	DLXNode* get_node();
	DLXNode* get_min_col();

	bool judgeRowCodeByCol(INT64 *rowCode, int colIdx);
	void updateRowCodeByCol(INT64 *rowCode, int colIdx);
	void updateRowCodeByRowCode(INT64 *rowCode, INT64 *srcRowCode);
	int get_eval();                // 估价函数

	void cover(DLXNode *colPtr);
	void uncover(DLXNode *colPtr);

	void coverRow(DLXNode *nodePtr);
	void uncoverRow(DLXNode *nodePtr);

	bool isEmpty();
public:
	                       
	void init(int r, int c, int limitC, eCoverType ect);
	void add(int rowIdx, int colIdx);       // index 0-based
	void output();
	bool dance(int depth, int maxDepth);
	void preCoverRow(int rowIndex);

	static DLX& Instance() {
		static DLX inst;
		return inst;
	}
};

void DLX::reset_col() {
	// [0, colCount)作为列首元素，
	// 第colCount个列首元素的地址作为总表头head
	for(int i = 0; i <= colCount; ++i) {
		DLXNode *colPtr = &col[i];
		colPtr->resetCol(i);
		// 初始化，每列元素为空，所以列首指针上下循环指向自己
		colPtr->up = colPtr->down = colPtr;
		// 第i个元素指向第i-1个，当i==0，则指向第colCount个，构成循环
		colPtr->left = &col[(i+colCount)%(colCount+1)];
		// 第i个元素指向第i+1个，当i==colCount，则指向第0个，构成循环
		colPtr->right = &col[(i+1)%(colCount+1)];
		col_coverd[i] = 0;
	}
	// 取第colCount个列首元素的地址作为总表头
	head = &col[colCount];
}

void DLX::reset_row() {
	for(int i = 0; i < rowCount; ++i) {
		// 初始化行首结点
		DLXNode *rowPtr = &row[i];
		// 初始化行，每行都为空，所以结点的各个指针都指向自己
		rowPtr->left = rowPtr->right = rowPtr->up = rowPtr->down = rowPtr;
		// 对应cover时候的函数入口的非空判断
		rowPtr->setColHead(NULL);
		rowPtr->setRowIdx(i);
		for(int j = 0; j < MAXROWCODE; ++j) {
			row_code[i*MAXROWCODE + j] = 0;
		}
	}
}

DLXNode* DLX::get_node() {
	return &dlx_pool[dlx_pool_idx++];
}

void DLX::init(int r, int c, int limitC, eCoverType ect) {
	reset_size(r, c, limitC, ect);
	reset_row();
	reset_col();
}

DLXNode* DLX::get_min_col() {
	DLXNode *resPtr = head->right;
	for(DLXNode *ptr = resPtr->right; ptr != head; ptr = ptr->right) {
		if(ptr->getColIdx() >= limitColCount)
			break;
		if(ptr->getColSum() < resPtr->getColSum()) {
			resPtr = ptr;
		}
	}
	return resPtr;
}

bool DLX::judgeRowCodeByCol(INT64 *rowCode, int colIdx) {
	int i;
	for(i = 0; i < MAXROWCODE; i++) {
		if(i*MAXB <= colIdx && colIdx < (i+1)*MAXB) {
			colIdx -= i*MAXB;
			return (rowCode[i] & ((INT64)1<<colIdx)) > 0;
		}
	}
	return false;
}

void DLX::updateRowCodeByCol(INT64 *rowCode, int colIdx) {
	int i;
	for(i = 0; i < MAXROWCODE; i++) {
		if(i*MAXB <= colIdx && colIdx < (i+1)*MAXB) {
			colIdx -= i*MAXB;
			rowCode[i] |= ((INT64)1<<colIdx);
			return;
		}
	}
}

void DLX::updateRowCodeByRowCode(INT64 *rowCode, INT64 *srcRowCode) {
	int i;
	for(i = 0; i < MAXROWCODE; i++) {
		rowCode[i] |= srcRowCode[i];
	}
}

/*
	功能：估价函数
	注意：估计剩余列覆盖完还需要的行的个数的最小值 <= 实际需要的最小值
*/
int DLX::get_eval() {
	int eval = 0;
	INT64 rowCode[MAXROWCODE];
	DLXNode *colPtr;
	memset(rowCode, 0, sizeof(rowCode));

	// 枚举每一列
	for(colPtr = head->right; colPtr != head; colPtr = colPtr->right) {
		int colIdx = colPtr->getColIdx();
		if(!judgeRowCodeByCol(rowCode, colIdx)) {
			updateRowCodeByCol(rowCode, colIdx);
			++eval;
			// 枚举该列上的么个元素
			for(DLXNode *nodePtr = colPtr->down; nodePtr != colPtr; nodePtr = nodePtr->down) {
				updateRowCodeByRowCode(rowCode, &row_code[nodePtr->getRowIdx()*MAXROWCODE]);
			}
		}
	}
	return eval;
}

/*
	功能：插入一个(rowIdx, colIdx)的结点（即原01矩阵中(rowIdx, colIdx)位置为1的）
	注意：按照行递增、列递增的顺序进行插入
*/
void DLX::add(int rowIdx, int colIdx) {
	DLXNode *nodePtr = get_node();
	// 将结点插入到对应列尾
	nodePtr->appendToCol(&col[colIdx]);
	// 将结点插入到对应行尾
	nodePtr->appendToRow(&row[rowIdx]);
	updateRowCodeByCol(&row_code[MAXROWCODE*rowIdx], colIdx);
}

/*
	功能：输出当前矩阵
	调试神器
*/
void DLX::output() {
	for(int i = 0; i < rowCount; i++) {
		DLXNode *rowPtr = &row[i];
		printf("row(%d)", i);
		for(DLXNode *nodePtr = rowPtr->right; nodePtr != rowPtr; nodePtr = nodePtr->right) {
			printf(" [%d]", nodePtr->getColHead()->getColIdx());
		}
		puts("");
	}
}

/*
	功能：删除行
		  精确覆盖在删除列的时候，需要对行进行删除处理
		  枚举每个和nodePtr在同一行的结点p，执行删除操作 
*/
void DLX::coverRow(DLXNode* nodePtr) {
	for(DLXNode *p = nodePtr->right; p != nodePtr; p = p->right) {
		p->deleteFromRow();
	}
}

/*
	功能：恢复行
		coverRow的逆操作 
*/
void DLX::uncoverRow(DLXNode* nodePtr) {
	for(DLXNode *p = nodePtr->left; p != nodePtr; p = p->left) {
		p->resumeFromRow();
	}
}

/*
	功能：覆盖colPtr指向的那一列
		 说是覆盖，其实是删除那一列。
		 如果是精确覆盖，需要删除那列上所有结点对应的行，原因是，cover代表我会选择这列，这列上有1的行必须都删除
*/
void DLX::cover(DLXNode *colPtr) {
	if(!colPtr) {
		return;
	}
	if(!col_coverd[colPtr->getColIdx()]) {
		// 删除colPtr指向的那一列
		colPtr->deleteFromCol();
		// 枚举每个在colPtr对应列上的结点p
		if (eCType == ECT_EXACT) {
			for(DLXNode* nodePtr = colPtr->down; nodePtr != colPtr; nodePtr = nodePtr->down) {
				coverRow(nodePtr);
			}
		}	
	}
	++col_coverd[colPtr->getColIdx()];
}

/*
	功能：恢复colPtr指向的那一列
		 cover的逆操作
*/
void DLX::uncover(DLXNode* colPtr) {
	if(!colPtr) {
		return;
	}
	--col_coverd[colPtr->getColIdx()];
	if(!col_coverd[colPtr->getColIdx()]) {
		// 枚举每个在colPtr对应列上的结点p
		if (eCType == ECT_EXACT) {
			for(DLXNode* nodePtr = colPtr->up; nodePtr != colPtr; nodePtr = nodePtr->up) {
				uncoverRow(nodePtr);
			}
		}
		// 恢复colPtr指向的那一列
		colPtr->resumeFromCol();
	}
}

/*
	功能：用于预先选择某行 
*/
void DLX::preCoverRow(int rowIndex) {
	DLXNode *rowPtr = &row[rowIndex];
	for(DLXNode *p = rowPtr->right; p != rowPtr; p = p->right) {
		cover(p->getColHead());
	}
}

bool DLX::isEmpty() {
	if(head->right == head) {
		return true;
	}
	return head->right->getColIdx() >= limitColCount;
}

bool DLX::dance(int depth, int maxDepth=INF) {
	if(minResultCount != -1 && depth > minResultCount) {
		return false;
	}
	// 当前矩阵为空，说明找到一个可行解，算法终止 
	if(isEmpty()) {
		resultCount = depth;
		if(minResultCount == -1 || resultCount < minResultCount) {
			minResultCount = resultCount;
		}
		return false;
	}
	if (maxDepth != INF) {
		if(depth + get_eval() > maxDepth) {
			return false;
		}
	}

	DLXNode *minPtr = get_min_col();
	// 删除minPtr指向的列 
	cover(minPtr);
	// minPtr为结点数最少的列，枚举这列上所有的行
	for(DLXNode *p = minPtr->down; p != minPtr; p = p->down) {
		// 令r = p->getRowIdx()，行r放入当前解 
		result[depth] = p->getRowIdx();
		// 行r上的结点对应的列进行删除 
		for(DLXNode *q = p->right; q != p; q = q->right) {
			cover(q->getColHead());
		}
		// 进入搜索树的下一层 
		if(dance(depth+1, maxDepth)) {
			return true;
		}
		// 行r上的结点对应的列进行恢复 
		for(DLXNode *q = p->left; q != p; q = q->left) {
			uncover(q->getColHead());
		}
	}
	// 恢复minPtr指向的列
	uncover(minPtr); 
	return false;
}

#define MAXN 35
int rowCnt, colCnt;
int colIdx[MAXN][MAXN];
int dlx_mat[MAXR][MAXC];

int X, Y, p;

int main() {
	int t;
	int i, j;
	scanf("%d", &t);
	while(t--) {
		scanf("%d %d %d", &X, &Y, &p);
		colCnt = 0;
		for(i = 0; i < X; ++i) {
			for(j = 0; j < Y; ++j) {
				colIdx[i][j] = colCnt++;
			}
		}
		memset(dlx_mat, 0, sizeof(dlx_mat));
		rowCnt = p;
		for(i = 0; i < p; i++) {
			int x1, y1, x2, y2;
			scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
			for(int x = x1; x < x2; ++x) {
				for(int y = y1; y < y2; ++y) {
					dlx_mat[i][ colIdx[x][y] ] = 1;
				}
			}
		}
		DLX &dlx = DLX::Instance();
		dlx.init(rowCnt, colCnt, INF, ECT_EXACT);
		for(i = 0; i < rowCnt; ++i) {
			for(j = 0; j < colCnt; ++j) {
				if(dlx_mat[i][j]) {
					dlx.add(i, j);
					//printf("<%d, %d>\n", i, j);	
				}
			}
		}
		dlx.dance(0);
		printf("%d\n", dlx.minResultCount); 
	}
	return 0;
}