【深度学习】4-3 误差反向传播法 - Affine/Softmax层的实现

Affine层

神经网络的正向传播中进行的矩阵的乘积运算(也就是Y = np.dot(X, W) + B)在几何学领域被称为“仿射变换”。因此，这里将进行仿射变换的处理实现为“Affine层”。

几何中，仿射变换包括一次线性变换和一次平移，分别对应神经网络的加权和运算与加偏置运算。

下面考虑上面计算图的反向传播，可以得到下面的式子：

根据上面的式子，尝试画出计算图的反向传播

这里要特别注意矩阵的形状，因为矩阵的乘积运算要求对应维度的元素数保持一致，通过确认一致性。
因此这个特点可以推导出矩阵的乘积的反向传播

批版本的Affine层
前面介绍的Affine层的输入X是以单个数据为对象的。现在我们考虑N个数据一起进行正向传播的情况，也就是批版本的Affine层。
下面是计算图

加上偏置时，需要特别注意。正向传播时，偏置被加到X·W的各个数据上。
正向传播时，偏置会被加到每一个数据(第1个、第2个…)上。因此反向传播时，各个数据的反向传播的值需要汇总为偏置的元素。用代码显示如下：

>>> dY = np.array([[1，2,3,],[4，5，6]])
>>> dY
array([[1，2，3],[4，5，6]])
>>>
>>> dB = np.sum(dY，axis=0)
>>> dB
array([5，7，9])

这个例子中，假定数据有2个(N=2)。偏置的反向传播会对这2个数据的导数按元素进行求和。因此，这里使用了np.sum()对第0轴方向上的元素进行求和

综上所述，Affine的实现如下所示：

class Affine:
	def __init__(self,W,b):
		self.W = W
		self.b = b
		self.x = None
		self.dW = None
		self.db = None

	def forward(self,x):
		self.x = x
		out = np.dot(x, self.W) + self.b
		return out

	def backward(self, dout):
		dx = np.dot(dout, sellf.W.T)
		self.dW = np.dot(self.x.T, dout)
		self.db = np.sum(dout, axis = 0)

Softmax-with-Loss 层

手写数字识别时，Softmax 层的输出如图：

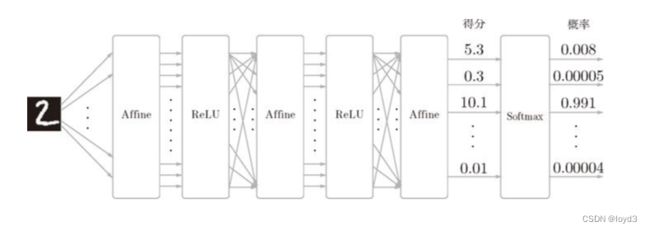
输入图像通过 Affine 层和 ReLU 层进行转换，10 个输入通过 Softmax 层进行正规化。在这个例子中，“0”的得分是 5.3，这个值经过 Softmax 层转换为 0.008（0.8%）；“2”的得分是 10.1，被转换为 0.991（99.1%）
在上图中，Softmax 层将输入值正规化（将输出值的和调整为 1）之后再输出。另外，因为手写数字识别要进行 10 类分类，所以向Softmax 层的输入也有 10 个。

下面来实现 Softmax 层。考虑到这里也包含作为损失函数的交叉熵误差（cross entropy error），所以称为“Softmax-with-Loss 层”。

可以看到，Softmax-with-Loss 层有些复杂。这里只给出了最终结果
鉴于上面的计算图过于复杂，将其简化为如下图：

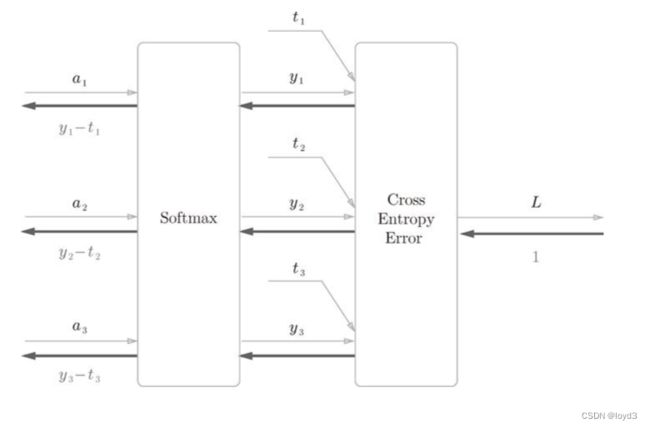
softmax 函数记为 Softmax 层，交叉熵误差记为 Cross Entropy Error 层。这里假设要进行 3 类分类，从前面的层接收 3 个输入（得分）。如图所示，Softmax 层将输入 正规化，Cross Entropy Error 层接收 Softmax 的输出 和教师标签 ( t₁,t₂,t₃) ，从这些数据中输出损失 L。

注意的是反向传播的结果。Softmax 层的反向传播得到了 (y₁-t₁, y₂-t₂, y₃-t₃)这样“漂亮”的结果。由于(y₁, y₂, y₃) 是 Softmax 层的输出，(t₁, t₂, t₃)是监督数据，所以(y₁-t₁, y₂-t₂, y₃-t₃) 是 Softmax 层的输出和教师标签的差分。神经网络的反向传播会把这个差分表示的误差传递给前面的层，这是神经网络学习中的重要性质。

神经网络学习的目的就是通过调整权重参数，使神经网络的输出(Softmax的输出)接近监督标签。因此，必须将神经网络的输出与监督标签的误差高效地传递给前面的层。刚刚的 (y₁-t₁, y₂-t₂, y₃-t₃)正是 Softmax层的输与监督标签的差，直截了当地表示了当前神经网络的输出与监督标签的误差。

如果这个误差大，Softmax层前面的层会从这个大的误差中学习到“大”的内容。
如果这个误差小，Softmax层前面的层会从这个大的误差中学习到“小”的内容。

下面来看Softmax-with-Loss层的实现，实现过程如下：

class SoftmaxWithLoss: 
	def __init__(self):
		self.loss = None
		self.y = None
		self.t = None

	def forward(self, x, t):
		self.t = t
		self.y = softmax(y)
		self.loss = cross_entropy_error(self.y, self,t)

		return self.loss

	def backward(self, dout=1):
		batch_size = self.t.shape[0]
		dx = (self.y - self.t) / batch_size
		
		return dx