遗传算法解决TSP旅行商问题（numpy、pandas）

努力是为了不平庸~

学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。

目录

一、引言

原理：

问题：

二、思路步骤

 三、代码编写步骤

A、代码各步骤的方法、目的及意义

1. 导入所需的库：

2. 处理数据部分：

3. 得到距离矩阵部分：

4. 设置遗传算法的参数：

5. 计算适应度函数：

6. 初始化种群的改良：

7. 自然选择：

8. 交叉繁殖：

9. 变异操作：

10.get_result的函数

11.初始化种群

12.迭代过程

13.将最优个体的路径转换为城市的顺序

14.绘制结果

B、遗传算法求解TSP问题的流程图

 四、完整代码

data数据集

---

一、引言

原理：

旅行商问题，即TSP问题（Traveling Salesman Problem）是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路经的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个组合优化问题。该问题可以被证明具有NPC计算复杂性。因此，任何能使该问题的求解得以简化的方法，都将受到高度的评价和关注。

遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程。它把问题的参数用基因代表，把问题的解用染色体代表（在计算机里用二进制码表示），从而得到一个由具有不同染色体的个体组成的群体。这个群体在问题特定的环境里生存竞争，适者有最好的机会生存和产生后代。后代随机化地继承了父代的最好特征，并也在生存环境的控制支配下继续这一过程。群体的染色体都将逐渐适应环境，不断进化，最后收敛到一族最适应环境的类似个体，即得到问题最优的解。要求利用遗传算法求解TSP问题的最短路径。

问题：

1、参考实验系统给出的遗传算法进行相关操作，用遗传算法求解TSP的优化问题，分析遗传算法求解不同规模TSP问题的算法性能。

2、对于同一个TSP问题，分析种群规模、交叉概率和变异概率对算法结果的影响。

3、画出遗传算法求解TSP问题的流程图。

4、分析遗传算法求解不同规模的TSP问题的算法性能。

5、对于同一个TSP问题，分析种群规模、交叉概率和变异概率对算法结果的影响。

二、思路步骤

1. 在数据处理和距离矩阵计算之后，我们定义了一些算法中需要用到的参数，如种群数、迭代次数、最优选择概率、弱者生存概率、变异率等。

2. 然后，我们定义了一个计算个体适应度（路径长度）的函数get_total_distance(x)。该函数遍历个体中的每个城市，计算城市之间的距离，并累加得到总路径长度。

3. 接下来，我们定义了一个改良函数gailiang(x)，用于对初始种群中的个体进行改良。该函数随机选择两个城市，并交换它们的位置，如果改良后的个体路径长度更短，则更新个体。

4. 然后，我们定义了自然选择函数nature_select(population)。该函数根据个体的适应度对种群进行排序，并选择适应度较高的个体作为强者，按照最优选择概率将一部分适应度较低的个体作为弱者生存下来。

5. 接下来，我们定义了交叉繁殖函数crossover(parents)。该函数从父代中随机选择两个个体，并随机选择一个交叉点，将交叉点之间的基因片段进行交换，生成两个子代个体。

6. 然后，我们定义了变异操作函数mutation(children)。该函数遍历子代个体，根据变异率随机选择两个基因位置，并交换它们的值，引入随机性，增加种群的多样性。

7. 在遗传算法的主要操作完成后，我们初始化种群，并开始进行迭代优化。在每一代中，我们先进行自然选择操作，选择适应度较高的个体作为父代。然后通过交叉繁殖操作生成子代个体。接下来，对子代个体进行变异操作。最后，更新种群，将父代和子代个体合并为新的种群。

8. 在每一代结束后，我们计算种群中最优个体的适应度和路径长度，并将路径长度添加到distance_list列表中。

9. 通过迭代多次，并持续更新种群，我们逐渐找到适应度最高的个体，即解决TSP问题的最优路径。

10. 最后，我们将最优路径的顺序和对应的距离打印出来，并绘制优化过程的图表，展示路径的变化和优化的进程。

通过这样的迭代过程，遗传算法能够逐步优化种群，找到适应度最高的个体，即最优路径。

 三、代码编写步骤

A、代码各步骤的方法、目的及意义

1. 导入所需的库：

    

 这些库用于数值计算、数据处理、绘图和随机数生成等功能。

2. 处理数据部分：

 这部分代码用于读取文件中的坐标数据，并将其存储在名为coordinates的NumPy数组中。首先，打开文件并逐行读取文件内容，然后对每一行进行分割，将得到的坐标值添加到coord列表中。接下来，将coord列表转换为NumPy数组，并初始化一个全零的数组coordinates，其大小与coord数组相同。最后，将coord数组中的坐标值转换为浮点型，并将其存储到coordinates数组中。

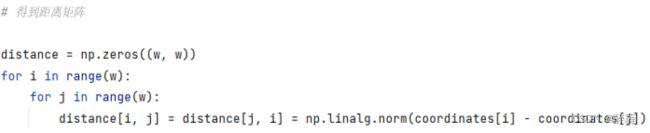
3. 得到距离矩阵部分：

 这部分代码用于计算城市之间的欧几里得距离，并构建距离矩阵。首先，创建一个全零的二维数组distance，大小为(w, w)，其中w为城市的数量。然后，使用两层循环遍历所有城市的组合，并计算每对城市之间的欧氏距离。最后，将计算得到的距离赋值给distance矩阵中对应的位置，并保证对称性，即同时更新对称位置的距离值。

这样，我们完成了数据的处理和距离矩阵的计算。接下来，我们将进行遗传算法的求解过程。

4. 设置遗传算法的参数：

 这些参数用于控制遗传算法的运行。count表示种群中个体的数量，iter_time表示遗传算法的迭代次数，retain_rate表示适应度最高的个体被选中的概率，random_select_rate表示适应度较低的个体被选中的概率，mutation_rate表示变异的概率，gailiang_N表示改良迭代的次数。

5. 计算适应度函数：

 这个函数用于计算给定路径x的总距离。它遍历路径中的每个城市，计算当前城市与下一个城市之间的距离，并累加到总距离中。如果当前城市是路径的最后一个城市，那么它会计算最后一个城市与起始城市之间的距离。

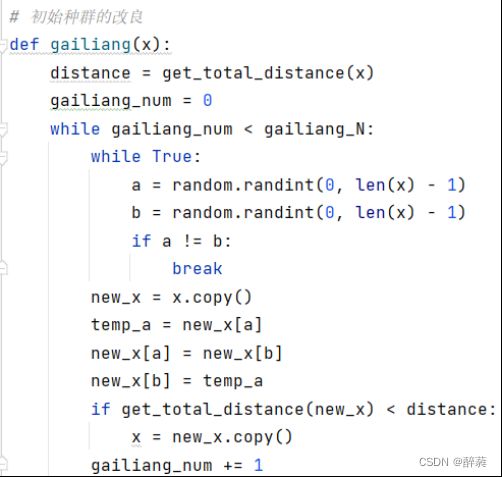
6. 初始化种群的改良：

 这个函数用于改良初始种群中的个体。它通过随机选择两个城市，并交换它们的位置来生成新的路径。如果新路径的总距离比原路径的总距离要小，那么将新路径替换原路径，从而实现改良。该过程会重复执行gailiang_N次，以提高种群的质量。

现在，已经准备好进行遗传算法的主要步骤。接下来，将进行自然选择、交叉繁殖和变异操作，以优化种群中的个体。

7. 自然选择：

 这个函数用于根据个体的适应度进行自然选择。首先，根据每个个体的适应度值进行排序，然后选择适应度较高的一部分个体作为"强者"存活下来。然后，对适应度较低的个体，以一定的概率进行选择，使它们有机会存活下来。最终返回存活下来的个体作为下一代的父代。

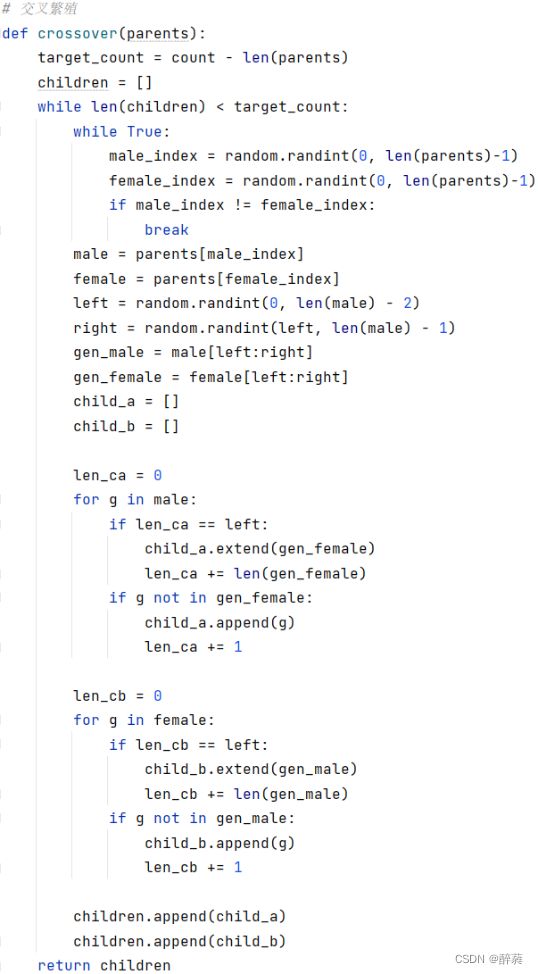
8. 交叉繁殖：

 这个函数用于进行交叉繁殖操作。从父代中随机选择两个个体作为父母，然后通过随机选择一个交叉点将父母的基因进行交叉，生成两个子代。交叉点左侧的基因保持不变，右侧的基因从另一个父母中获得。这样可以保留父代中的一部分特征，并引入新的基因组合，增加种群的多样性。

9. 变异操作：

 这个函数用于进行变异操作。遍历每个子代个体，根据变异率决定是否进行变异。如果进行变异，随机选择两个基因位置，并交换它们的值。通过变异操作，可以引入一些随机性，增加种群的多样性，有助于避免局部最优解。

以上三个步骤组成了遗传算法的主要操作，通过多次迭代和优化，逐渐找到适应度最高的个体，即解决TSP问题的最优路径。

10.get_result的函数

 这部分代码定义了一个名为 get_result的函数。该函数接受一个种群作为参数，并返回种群中适应度最佳的个体及其对应的适应度值。首先，通过遍历种群中的每个个体，使用 `get_total_distance` 函数计算个体的总距离，并将个体及其适应度值存储在二维列表 grad 中。然后，使用sorted函数对grad列表进行排序，按照适应度值从小到大进行排序。最后，通过返回grad[0][0]和grad[0][1]，即最佳个体和对应的适应度值。

11.初始化种群

这部分代码用于初始化种群。首先，创建一个空列表population，用于存储种群中的个体。然后，通过循环range(count)来生成一定数量的个体。在每次循环中，首先复制城市索引列表index，确保每个个体都有相同的初始顺序。接下来，使用random.shuffle函数对个体的顺序进行随机打乱，以增加种群的多样性。最后，调用gailiang函数对个体进行改良操作，进一步优化个体的排列顺序，并将个体添加到种群中。

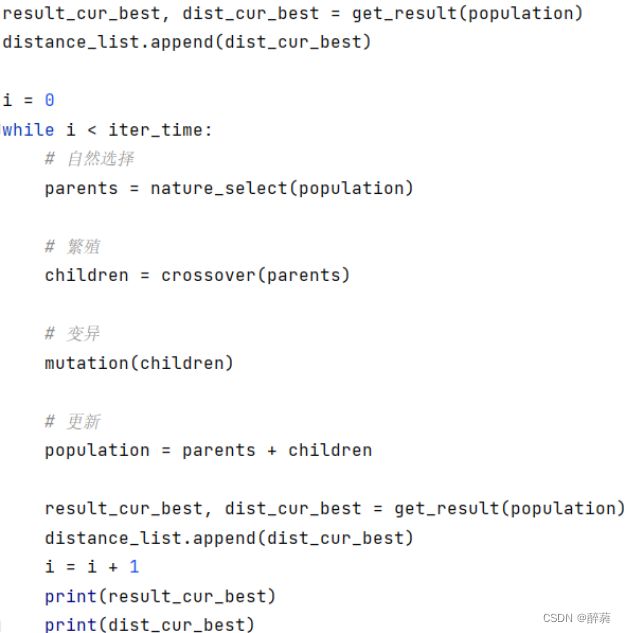
12.迭代过程

这部分代码是遗传算法的主要迭代过程。首先，创建一个空列表distance_list，用于存储每次迭代后种群中最优个体的适应度值。接下来，调用get_result函数，获取当前种群中适应度最好的个体及其适应度值，并将适应度值添加到distance_list列表中。

然后，使用while循环进行遗传算法的多次迭代。在每次迭代中，依次执行以下步骤：

①自然选择：调用nature_select函数对当前种群进行自然选择，选择出一部分优秀的个体作为父代。

②繁殖：调用crossover函数对父代个体进行交叉繁殖，生成一定数量的子代个体。

③变异：调用mutation函数对子代个体进行变异操作，引入一些随机性，增加种群的多样性。

④更新：将父代个体和子代个体合并，形成新的种群。

⑤获取最优个体：调用get_result函数，获取更新后种群中适应度最好的个体及其适应度值。

⑥记录适应度值：将适应度值添加到distance_list列表中。

⑦迭代次数计数：递增迭代计数器i。

在每次迭代中，打印当前迭代中种群中适应度最好的个体及其适应度值。

13.将最优个体的路径转换为城市的顺序

这部分代码用于将最优个体的路径转换为城市的顺序，并构建闭合路径。首先，使用for循环遍历result_cur_best列表中的每个元素，将其值加1。这是因为在之前的处理中，城市的索引从0开始，而在输出路径中，我们希望城市的编号从1开始。

然后，将更新后的result_cur_best赋值给result_path变量。接下来，将result_path列表的第一个元素添加到列表末尾，形成闭合路径。这是因为 TSP 问题中，旅行必须回到起始城市。打印输出result_path，即最优路径。

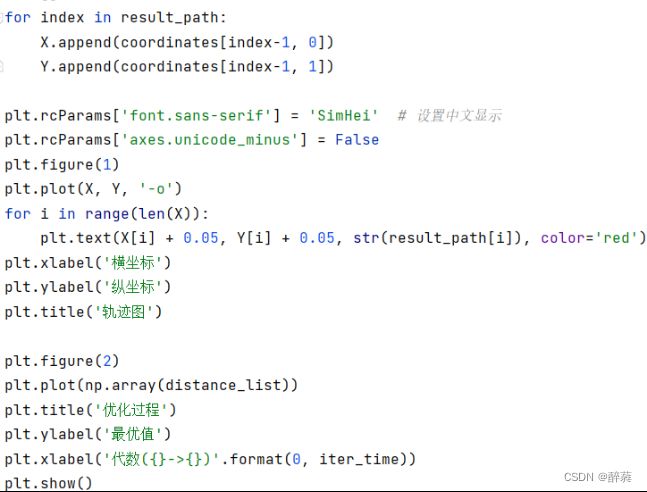
14.绘制结果

这部分代码用于绘制结果的可视化图形。首先，创建空列表X和Y用于存储每个城市的横纵坐标。通过遍历result_path列表中的每个元素，将对应城市的坐标添加到X和 Y中。

 

接下来，设置 matplotlib 的字体显示为中文，并创建两个图形窗口。在第一个图形窗口中，使用plot函数绘制城市路径，通过设置线条样式为 -o实现连接城市并在每个城市处绘制圆点。使用text函数在每个城市的位置添加城市编号。设置横纵坐标的标签和标题。

在第二个图形窗口中，使用plot函数绘制优化过程中的最优值变化，即distance_list列表。设置横纵坐标的标签和标题。

最后，使用show函数显示图形。

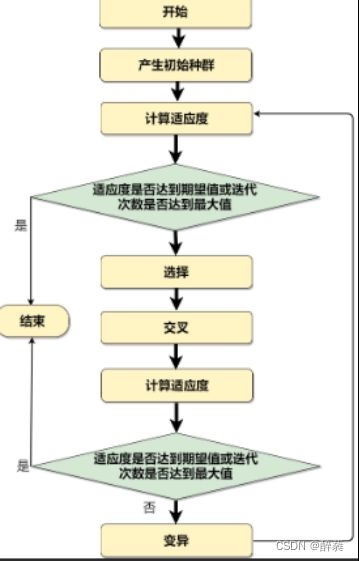
B、遗传算法求解TSP问题的流程图

 四、完整代码

#遗传算法求解TSP问题完整代码：
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
import math
import random

# 处理数据

coord = []
with open("data.txt", "r") as lines:
    lines = lines.readlines()
for line in lines:
    xy = line.split()
    coord.append(xy)

coord = np.array(coord)
w, h = coord.shape
coordinates = np.zeros((w, h), float)
for i in range(w):
    for j in range(h):
        coordinates[i, j] = float(coord[i, j])

# print(coordinates)

# 得到距离矩阵

distance = np.zeros((w, w))
for i in range(w):
    for j in range(w):
        distance[i, j] = distance[j, i] = np.linalg.norm(coordinates[i] - coordinates[j])

# 种群数
count = 300

# 进化次数
iter_time = 1000

# 最优选择概率
retain_rate = 0.3  # 适应度前30%可以活下来

# 弱者生存概率
random_select_rate = 0.5

# 变异
mutation_rate = 0.1

# 改良
gailiang_N = 3000


# 适应度
def get_total_distance(x):
    dista = 0
    for i in range(len(x)):
        if i == len(x) - 1:
            dista += distance[x[i]][x[0]]
        else:
            dista += distance[x[i]][x[i + 1]]
    return dista

# 初始种群的改良
def gailiang(x):
    distance = get_total_distance(x)
    gailiang_num = 0
    while gailiang_num < gailiang_N:
        while True:
            a = random.randint(0, len(x) - 1)
            b = random.randint(0, len(x) - 1)
            if a != b:
                break
        new_x = x.copy()
        temp_a = new_x[a]
        new_x[a] = new_x[b]
        new_x[b] = temp_a
        if get_total_distance(new_x) < distance:
            x = new_x.copy()
        gailiang_num += 1


# 自然选择

def nature_select(population):
    grad = [[x, get_total_distance(x)] for x in population]
    grad = [x[0] for x in sorted(grad, key=lambda x: x[1])]
    # 强者
    retain_length = int(retain_rate * len(grad))
    parents = grad[: retain_length]
    # 生存下来的弱者
    for ruozhe in grad[retain_length:]:
        if random.random() < random_select_rate:
            parents.append(ruozhe)
    return parents


# 交叉繁殖
def crossover(parents):
    target_count = count - len(parents)
    children = []
    while len(children) < target_count:
        while True:
            male_index = random.randint(0, len(parents)-1)
            female_index = random.randint(0, len(parents)-1)
            if male_index != female_index:
                break
        male = parents[male_index]
        female = parents[female_index]
        left = random.randint(0, len(male) - 2)
        right = random.randint(left, len(male) - 1)
        gen_male = male[left:right]
        gen_female = female[left:right]
        child_a = []
        child_b = []

        len_ca = 0
        for g in male:
            if len_ca == left:
                child_a.extend(gen_female)
                len_ca += len(gen_female)
            if g not in gen_female:
                child_a.append(g)
                len_ca += 1

        len_cb = 0
        for g in female:
            if len_cb == left:
                child_b.extend(gen_male)
                len_cb += len(gen_male)
            if g not in gen_male:
                child_b.append(g)
                len_cb += 1

        children.append(child_a)
        children.append(child_b)
    return children


# 变异操作
def mutation(children):
    for i in range(len(children)):
        if random.random() < mutation_rate:
            while True:
                u = random.randint(0, len(children[i]) - 1)
                v = random.randint(0, len(children[i]) - 1)
                if u != v:
                    break
            temp_a = children[i][u]
            children[i][u] = children[i][v]
            children[i][v] = temp_a


def get_result(population):
    grad = [[x, get_total_distance(x)] for x in population]
    grad = sorted(grad, key=lambda x: x[1])
    return grad[0][0], grad[0][1]


population = []
# 初始化种群
index = [i for i in range(w)]
for i in range(count):
    x = index.copy()
    random.shuffle(x)
    gailiang(x)
    population.append(x)

distance_list = []
result_cur_best, dist_cur_best = get_result(population)
distance_list.append(dist_cur_best)

i = 0
while i < iter_time:
    # 自然选择
    parents = nature_select(population)

    # 繁殖
    children = crossover(parents)

    # 变异
    mutation(children)

    # 更新
    population = parents + children

    result_cur_best, dist_cur_best = get_result(population)
    distance_list.append(dist_cur_best)
    i = i + 1
    print(result_cur_best)
    print(dist_cur_best)


for i in range(len(result_cur_best)):
    result_cur_best[i] += 1

result_path = result_cur_best
result_path.append(result_path[0])

print(result_path)

# 画图
X = []
Y = []
for index in result_path:
    X.append(coordinates[index-1, 0])
    Y.append(coordinates[index-1, 1])

plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
plt.figure(1)
plt.plot(X, Y, '-o')
for i in range(len(X)):
    plt.text(X[i] + 0.05, Y[i] + 0.05, str(result_path[i]), color='red')
plt.xlabel('横坐标')
plt.ylabel('纵坐标')
plt.title('轨迹图')

plt.figure(2)
plt.plot(np.array(distance_list))
plt.title('优化过程')
plt.ylabel('最优值')
plt.xlabel('代数({}->{})'.format(0, iter_time))
plt.show()

data数据集

1.304 2.312
3.639 1.315
4.177 2.244
3.712 1.399
3.488 1.535
3.326 1.556
3.238 1.229
4.897 5.468
1.987 2.687
6.359 6.987
10.479 11.674
9.657 6.845
7.687 6.945
12.467 10.367
15.164 14.267
17.654 14.983
1.302 7.635
2.346 9.647
3.647 10.943
12.001 2.036
11.746 1.357
9.467 2.467
14.605 6.876
16.798 5.304
4.304 8.674
5.476 14.379
16.004 7.649