B-tree算法需求分析及实现
1. 基本需求
考虑在磁盘文件上存储一张数据表,每张表有很多记录,暂时假定每个记录所存储的空间长度是相同的,每个记录有一个唯一的索引。操作系统对文件的读写是以页为单位的,每页长度为4096字节,现在需要对这张表中的记录进行插入、查找、删除操作。
不考虑时间和内存的性能,最简单的思路就是遍历每一页,在页中遍历每一个记录,查找给定的记录,如果记录不在这一页中再查找下一页,删除时只要找到对应的记录将其清空即可,而插入操作更简单,遍历每一页找到空闲的记录地址,将数据写入到该地址即可。
应该说在数据量不大的时候,上述做法还是挺好的,思路清晰自然,实现起来也很简单,在性能上也并不会受到什么大的影响。
但是在数据量比较大的时候,相对来说顺序查找的速度会慢一些,一两次查找也不会感受到慢太多,但如果是成千上万次频繁查找,积累下来的时间就非常可观了,人会明显感觉到慢很多,这时我们就要考虑做一些优化了。
我们知道顺序查找的平均时间是O(N),二叉树查找的平均时间是O(log2N),那么能不能采用二叉树查找来缩短查找的时间呢?答案是否定的,因为二叉树只有2个子结点,每读取一个记录时都需要一次磁盘I/O 操作,树的深度较深,需要更多的磁盘I/O操作,但是磁盘的读写时间比内存要多的多,对于查找时间的最主要制约因素是磁盘文件的读写次数,所以即使总的搜索次数较少,如果磁盘I/O操作太频繁也是不行的。
这时我们发现B-tree结构正好能弥补二叉树的缺陷,B-tree是一种多叉树,一个父结点有很多个子结点,同一个父结点下的子结点组成一个磁盘块,每读取一页时就能一次性读取到多个记录,假设子结点的个数是m,则树的深度是O(logmN),这大大减少了对磁盘文件的读写。
2. 测试分析
为了能感受B-tree带来的好处,有必要对顺序查找做一个简单的测试来直观感受一下。先随机插入10条记录,每条记录占16字节,再做100次随机查找,然后随机删掉2条记录,重复上述操作,记录所需要的时间。
插入时隐含着一次查询,因为需要先查询来判读这条记录是否已经在表中了,如果在表中则表示记录存在冲突,不执行此次插入。删除时也隐含着一次查找,为了确定要删除记录在文件中的位置。
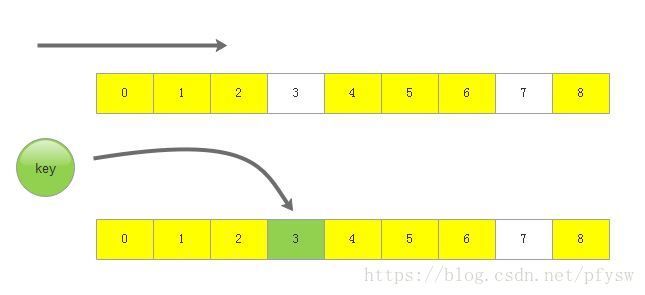
如下图所示,遍历整张表后发现key值不在表内,同时确定了第3个slot为空闲slot,然后把key插入到该位置。
测试平台为msys2和linux虚拟机:
顺序查找表测试时间
重复次数 |
msys2下时间 |
linux下时间 |
1000 |
13s |
6s |
2000 |
54s |
20s |
4000 |
213s |
59s |
10000 |
略 |
409 |
很显然根据上面的测试,顺序查询的效率非常低,而且文件数据量的增大,花费的时间基本呈指数增长。我们先看看不用btree算法有没有什么优化的方法。
在优化前要把握住2个最关键的因素,其中一个是减少硬盘的读写次数,因为内存的读写速度要远远快于磁盘的读写速度,另外在磁盘中读写数据,磁头的移动非常耗时间,所以顺序读写的时间远远快于随机读写,甚至在固态硬盘中顺序读写比内存的随机读写都要快很多。
根据以上2个问题,并针对上面的测试场景,我们来对插入、查找、删除分别做优化,现在先不考虑B-tree算法:
- 插入
每一次插入都要查询导致了磁盘的写数据不连续,所以可以先把要插入的10条记录保存到内存,进行统一查找确定没有冲突的记录,然后一次性写入到文件末尾,等到空闲的slot超过1000条时,再统一把后面的记录移到前面。在实际应用中,我们不知道什么时候会开始下一次插入操作,所以要做一个批量插入的接口。
- 查找
为了加快查找的速度,通常都是把数据按照一定的结构排序,但是我们上面的优化是按顺序写入数据,所以这种方法不行。那么有没有方法能使我们在查找之前就知道这个记录在不在表中呢?答案是有的,就是用bitmap算法把关键字映射到一个bit里,但是如果关键字太大的话用普通的bitmap算法将会非常耗内存,我在之前的文章里介绍过SQLite的bitmap算法可以解决这个问题,即需要多少记录使用多少内存。
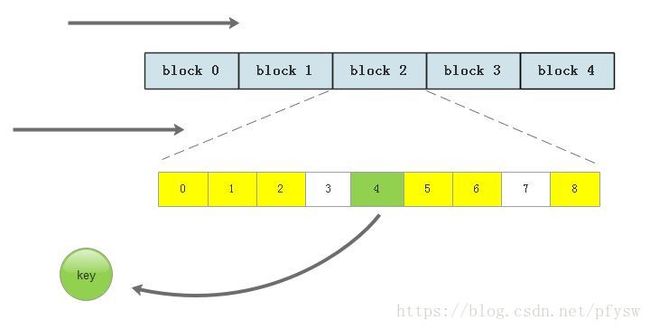
现在先假定最大记录数量为100万,此时最多需要消耗125K内存。我们把磁盘文件按块划分每10页即2560个记录组成一块,用bitmap先确定记录在哪一块,然后到对应的那一块里搜索,块的划分可以根据数据量和内存自行调整。
使用bitmap在提高搜索速度的同时更多是为了节省内存的考虑,如果不考虑内存,甚至可以建立一个超大数组,把关键字和记录在文件中的偏移位置做一个映射。
如下图所示,先遍历每一块,确定要查找的记录在第2块里,然后再遍历这一块的所有页中的所有slot
- 删除
删除操作没有什么好优化的,这就是一个建立在查找上的附加操作。
- 移动
每次插入时都是插入到文件的末尾,中间可能会有很多slot被删除,所以为了避免文件变得很大,当空闲slot到达1000时个时,就把后面的记录移到前面。
下表是经过优化后的测试数据
优化后的顺序查找表测试时间
重复次数 |
msys2下时间 |
linux下时间 |
1000 |
2s |
1s |
2000 |
4s |
4s |
4000 |
8s |
8s |
10000 |
22s |
18s |
算法的思路基本差不多,但是经过优化后发现速度提高了数10倍,所以写代码不能太随意,否则写出来的代码性能会非常差。
3. B-tree算法
上面已经对插入和查找做了一些优化,在查找虽然增加了bitmap分块定位来缩小查找范围,但是在每一块里基本还是顺序查找,而B-tree并不是顺序查找,而是一种特殊的二叉树查找,能够有效减少读取磁盘的次数,这是非常重要的,所以尽管B-tree写数据时是随机写入到磁盘,相比顺序写入性能会下降,但是大量应用都需要很多读操作,而写操作相对较少,所以写入性能变差也不那么关键了。
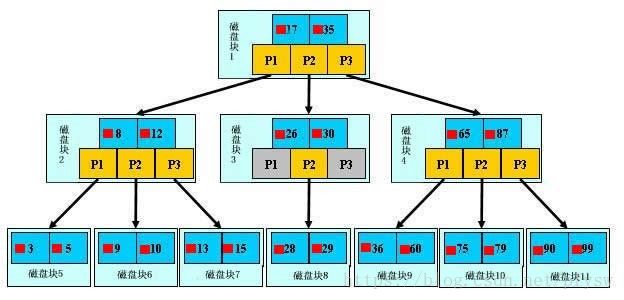
下面来简要介绍一下B-tree算法,B-tree其实就是一颗多叉树,即一个父结点会下挂很多个子结点,每个结点由关键字和子结点的指针组成,关键字里存储了所需的记录数据,每个结点里的关键字都是从小到大的顺序排列,而且如果我们把子结点中的关键字全部展开,这时候父结点和子结点的所有关键字也都是按顺序排列的,下图就是一个典型的B-tree
每一个磁盘块相当于一个B-tree的结点,蓝色区域是结点的关键字,黄色是子结点的指针,磁盘块里可能会有很多个关键字记录和子结点指针,我们先来看磁盘块2,关键字是8、12,子结点有P1,P2,P3,现在用子结点的关键字替代子结点的指针,得到全部关键字为3、5、8、9、10、12、13、15也是按照顺序排列的。
如果只是随便插入的话,经过多次插入和删除后这棵树就会退化成一张线性表,那么B-tree查找的优势也就不存在了,所以每一次插入都要使B-tree保持平衡,为了保持平衡B-tree会有以下一些特性,以一颗m阶B-tree(m叉树)为例:
- 树中每个结点至多有m个子结点
- 除根结点和叶子结点外,其他每个结点至少有[m/2]个子结点
- 若根结点不是叶子结点,则至少有2个子结点
- 所有叶子结点都出现在同一层
- 假设在某个非叶子结点里,子结点的个数为n,那么关键字的个数为n-1
- 所有结点的关键字个数范围为[m/2]-1~m-1
B-tree的查找比较简单,从根结点开始,按照关键字的大小定位目标结点在哪一个子结点里,层层往下搜索直到到达叶子结点,最后必定能找到目标。
插入和删除操作就有些繁琐,因为这会变更B-tree的结构,每次操作都要维持B-tree满足上面的特性。
下面来介绍B-tree的实现,这里以磁盘的每一页为一个结点,一页仍然是4096个字节,一页里有16字节的头部,接下来每一个记录为20个字节,其中16个字节为关键字和数据,另外4字节为子结点地址,一页里总共有(4096-16)/20=204个记录,即子结点个数最多为204个,关键字个数最多为203个,因为关键字个数要比子结点个数少1,所以最后一个记录只要子结点地址而没有关键字。
每个结点的定义如下:
struct Node
{
NodeHdr nodeHdr;//16字节头部
BtreeRecord aRecord[MAX_SUB_NUM];//204个记录
};头部包含了结点的属性,如是否是根结点或叶子结点,定义如下
typedef struct NodeHdr
{
u32 nPage;//页面数量,只用在第一次读取文件时从根结点获取
u32 reserve;
u8 aMagic[4];//校验值
u16 nRecord;//关键字个数
u8 isLeaf;//是否为叶子结点
u8 isRoot;//是否为根结点
}NodeHdr;每个记录的结构体定义如下
typedef struct BtreeRecord
{
int key;//关键字
u8 aMagic[4];
u8 aData[8];
u32 iSub;//关键字左边的子结点地址
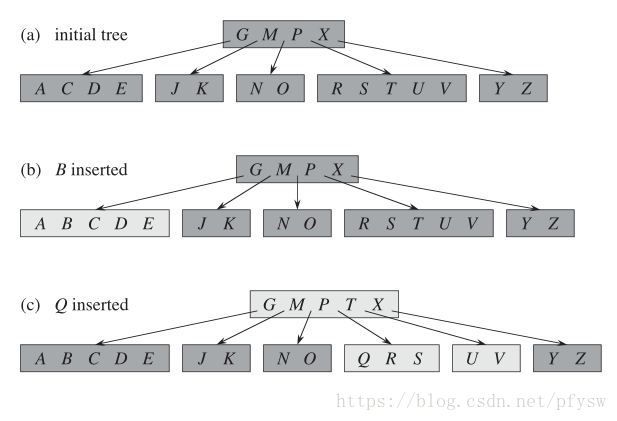
}BtreeRecord;插入的时候数据的时候找到要插入关键字所在的叶子结点插入,在查找过程中如果有发现要查找的非叶子结点关键字数量已经到达m-1,则对其进行分裂,而叶子结点在超过m-1时才分裂,这样接保证了在分裂后父节点的关键字数量不会超过m-1,下面假设m的值为6,插入过程如下图,插入B时的时候关键字个数还没有超过最大值,直接插入,插入Q的时候关键字个数超过最大值,则进行分裂,把中间关键字T提到父结点:
接下来要插入L时,内部结点(GMPTX)的关键字数量达到最大值,则先进行分裂,否则子树会在分裂后上提一个关键字到父结点,造成关键字数量超过限制。
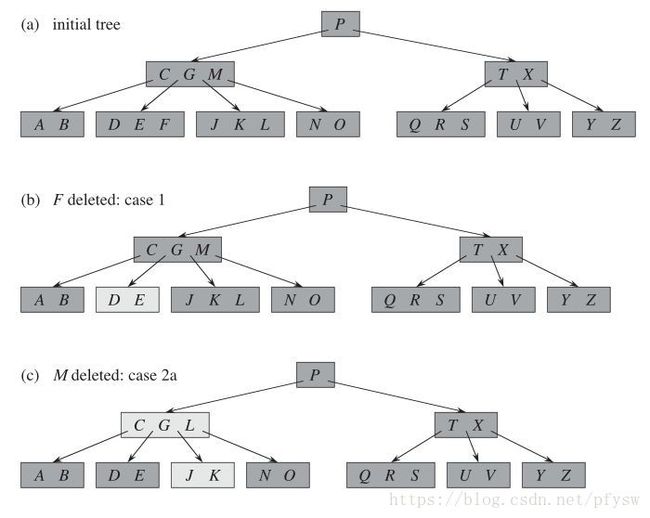
删除的操作就更加复杂了,情况分为很多种,基本思路就是先把结点删除了,如果关键字数量小于最小值2,再进行调整,整个删除过程如下图所示
(1)如图b,删除的记录在叶子结点,且不用调整,实现函数为
BtreeDeleteLeaf()
(2)如图c,删除的记录M在内部结点,向下从叶子结点中找到与M相邻的记录,如果关键字的数量有多余则将其上移到被删除的M位置,此处L上移到M,注意如果L不是叶子结点,L就不与M相邻,要继续向下搜索,实现函数为
BtreeDeleteInside()
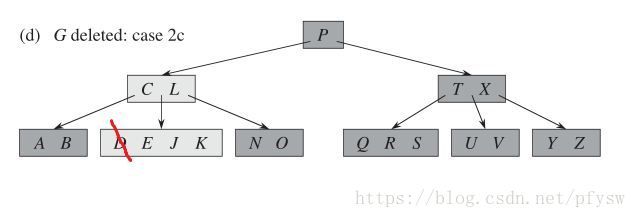
(3)如图c、d所示,要删除内部G,此时与M相邻的叶子结点已经没有多余的记录了,但是此时仍然把记录E或J上移到G的位置,这里假定是E,这时E所在结点已经小于最小关键字数量了,而且邻居结点的关键字数量也都到了最小值,那么找一个邻居结点合并,这里是J和K,实现函数为
BtreeDeleteInside()
BtreeAdjust()
mergeBtree()
(4)如图d所示,P的左右子结点的最大关键字数量都已经为最小值则将其合并,如图e所示。为了让工程实现更简单,这里只有等到(C、L)和(T、X)结点中被删关键字后从叶子结点补上来了一个关键字,但是又由于叶子结点向上层层合并触发了结点的记录数减小才合并。所以实际上,我写的代码在记录D被删除后并不触发合并,图e是《算法导论》的方案,仅作参考。
(5)在图e和图f中,B被删除,但是邻居结点(E、J、K)的记录数有多余,则把父结点C移到被删除的B位置,把E移到父结点,实现函数为
getNeighborKey()
(6) 在实现时无论是删除内部结点还是叶子结点,最后都会产生一个由根结点到叶子结点的搜素记录
pBt->aFind[pBt->iFind++]= pBt->iPage;
最后接可以由pBt->aFind和pBt->iFind从叶子结点开始回退到根结点,回退过程中遇到关键字数量小于最小值则或是情况(5)从邻居结点拿关键字或是情况(3)与邻居结点合并。
通过上面的分析就完成了Btree的查找和删除过程,接下来按照上一节讲到的测试方法来测试,测试结果如下,并与顺序表的处理时间做对比:
Btree数据处理测试时间
重复次数 |
msys2下时间 |
linux下时间 |
1000 |
0s |
0s |
2000 |
1s |
1s |
4000 |
3s |
2s |
10000 |
8s |
6s |
顺序表处理测试时间
重复次数 |
msys2下时间 |
linux下时间 |
||
优化后 |
未优化 |
优化后 |
未优化 |
|
1000 |
2s |
13s |
1s |
6s |
2000 |
4s |
54s |
4s |
20s |
4000 |
8s |
213s |
8s |
59s |
10000 |
22s |
略 |
18s |
409 |
最后结果可以看到Btree算法比优化后的顺序查找的性能都要提高了好几倍,这里最关键的因素就是Btree减少了大量磁盘的读取次数,因为磁盘读取是一个非常耗时间的操作。
4. 测试代码
测试代码的 github地址如下:
https://github.com/pfysw/btree
btree_test()测试Btree的插入、删除和查找操作;SequenceTest()测试顺序表的插入、删除和查找操作,其中SeqTest1()是未经优化的,SeqTest2()是优化后的。
代码是自己写的,应该还有许多不足,后续会借鉴其他开源代码中B-tree、B+-tree、LSM tree的处理来进一步优化