【Day6·超详细】数据结构 之 栈的应用 迷宫问题详解（包含详细举例）

导读

这篇文章将会非常详细介绍如何用栈去简单地找一个迷宫的路径

目录

导读

迷宫

准备工作

超详细举例

完整代码

---

 

迷宫

 这是一个迷宫，如果想让计算机去找一条从起点到终点的路径，通常利用“穷举求解”，先到达A，往下走到B，再到D，再到H，发现没有路了，回溯到D，再到I，没有路了回溯到D，再到J，没有路了，回溯到D再回溯到B，再到K......，最终回溯到A，再经过几次“撞墙”，终于到达终点。

通过这个简单的例子，可以看出，完成迷宫核心的思想是“回溯”，那么我们如何去保存之前走过的路径呢？由于回溯的起点是回溯前路径的终点，所以最好的办法是找一个“后进先出”的结构，所以我们可以利用栈这个东西。

大体步骤就是从起点开始，如果在方向一能前进，则将下一个坐标入栈，并继续前进，发现不能走的时候就出栈然后返回，在返回的路径上如果在某一个坐标处，除了之前走过的方向一，还有其它方向是通的，就可以走其它方向，将下一个坐标入栈，依次类推，到达终点直接打印。

准备工作

1.栈的构造，由于里面保存的是坐标，可以先定义一个Pos类型的结构体，包含着xy两个坐标，然后此处使用顺序栈，里面包含Pos类型的数组和int类型的栈顶标记top

2.方向定义，此处假设可以走8个方向，定义Pos类型的数组Pos dir[8]

3.迷宫定义，使用二维数组，0表示道路，1表示墙，例如：

 x 往下为正，y往右为正

4.定义一个和迷宫大小一样的二维数组mark记录是否经过某个坐标，0表示没经过可以走，1表示这条path已经包含了就不能再走了，否则会出现死循环，初始化为全0。

5.入栈、出栈函数的简单定义。

6.print函数的定义，传入两个参数，一个是int类型的sum，记录这是第几条路径（起点到终点可以有多条路径），一个是栈，用于输出打印路径（跟遍历相似）

超详细举例

比如，给出这么一个迷宫：

右边和下面分别是mark数组和栈

起点位于左上角的（1,1） 终点位于右下角的 （4,4）

刚开始，让（1,1）入栈，Mark标记：

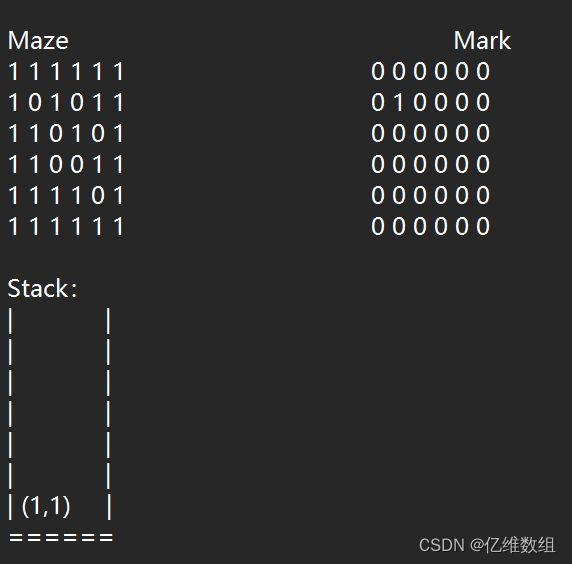第一个搜索的方向是右边，不能走，第二个换成右下角，可以走到达（2,2）并入栈：

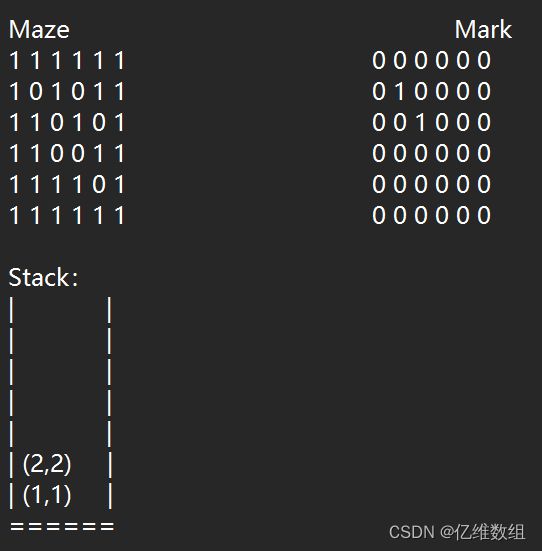在（2,2）处，同样也是先从右边搜索，不能走，然后走右下角，到达（3,3）入栈：

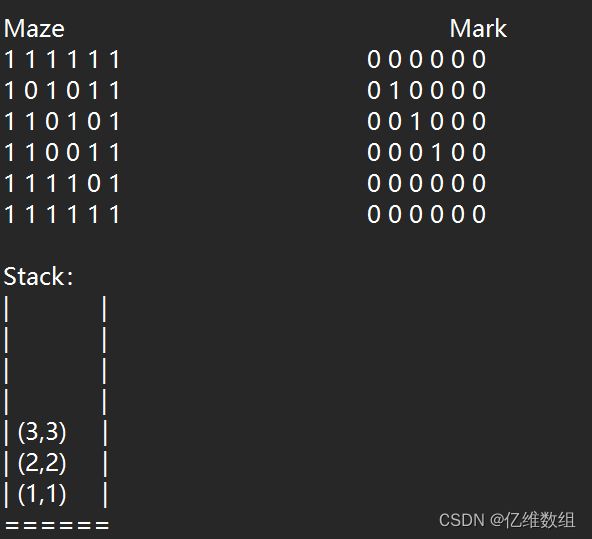在(3,3)处，也只能走右下角，直接到达终点，让（4,4）也入栈，让Mark（4,4）也变为1并得到第一条路：

path1：（1,1）——（2,2）——（3,3）——（4,4）

出栈（4,4）并把（4,4）的Mark变为0

然后回溯到（3,3），再搜索下面的位置，不能走，左下角，不能走，左边可以走，而且Mark（3,2）==0，可以入栈（3,2）并且标记Mark：

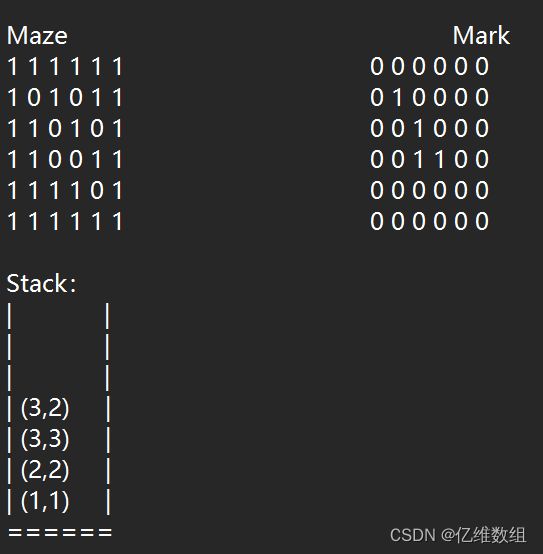在（3,2）处，也是先搜索右方，Mark（3,3）为1，不可以，同理，其它位置都不可以，所以（3,2）出栈，Mark（3,2）还原

在（3,3）处轮到了向左上角找，不行，上边，不行，右上角，可以！入栈，标记...到（2,4），（2,4）搜索发现（1,3）也行，但（1,3）的左下角（2,2）的Mark为1，所以这条路径报废，重新回到（3,3），（3,3）已经找完，出栈，回溯到（2,2），轮到（2,2）向下方找，入栈（3，2），再向右入栈（3,3）再到终点：

得到第二条路径

path2：（1,1）——（2,2）——（3,2）——（3,3）——（4,4）

其它同理，可以得到最后一条路径：（自行分析）

path3：（1,1）——（2,2）——（1,3）——（2,4）——（3,3）——（4,4）

 

完整代码

下面给出完整代码，大家可以复制，若有不足，还请指出：

#include
#include
#define MAXSIZE 100
#define m 6
#define n 8
typedef struct{
	int x;
	int y;
}Pos;
typedef struct{
	Pos data[MAXSIZE];
	int top;
}*StackPtr,Stack;
int sum=0;//记录路径的种类数
int Maze[m+2][n+2]={
	/*0,1,2,3,4,5,6,7,8,9*/
/*0*/  {1,1,1,1,1,1,1,1,1,1},
/*1*/  {1,0,1,1,1,0,1,1,1,1},
/*2*/  {1,1,0,1,0,1,1,1,1,1},
/*3*/  {1,0,1,0,0,0,0,0,1,1},
/*4*/  {1,0,1,1,1,0,1,1,1,1},
/*5*/  {1,1,0,0,1,1,0,0,0,1},
/*6*/  {1,0,1,1,0,0,1,1,0,1},
/*7*/  {1,1,1,1,1,1,1,1,1,1},
};
int Mark[m+2][n+2]={0};
StackPtr InitStack(void)  //初始化栈 
{
	StackPtr S=(StackPtr)malloc(sizeof(Stack));
	S->top=-1;
	return S;
}
void Push(StackPtr S,Pos e)//入栈 
{
	if(S->top==MAXSIZE-1)
	{
		printf("栈满！\n");
		return; 
	}
	S->top++;
	S->data[S->top]=e;
}
void Pop(StackPtr S,Pos *e)//出栈
{
	if(S->top==-1)
	{
		printf("空栈！\n");
		return; 
	}
	*e=S->data[S->top];
	S->top--;
}
void print(int sum,StackPtr S)
{
	int i;
	printf("第%d条路径为：");
	for(i=0;i<=S->top;i++)
	{
		printf("(%d,%d)--->",S->data[i].x,S->data[i].y);
	}
	printf("终点\n\n");
} 
Pos dir[8]={{0,1},{1,1},{1,0},{1,-1},{0,-1},{-1,-1},{-1,0},{-1,1}
};//八个方向，正右开始，顺时针旋转 
void Path(int x,int y,StackPtr S)
{
	if(x==6&&y==8)
	{
		sum++;
		print(sum,S);
	}
	else
	{
		int i;
		Pos temp;
		for(i=0;i<8;i++)
		{
			if(Maze[x+dir[i].x][y+dir[i].y]==0&&Mark[x+dir[i].x][y+dir[i].y])
			{
				temp.x=x+dir[i].x;
				temp.y=y+dir[i].y;
				Mark[x+dir[i].x][y+dir[i].y]=1;
				Push(S,temp);
				Path(x+dir[i].x,y+dir[i].y,S);
				Pop(S,&temp);
			}
		}
	}
}
int main()
{
	StackPtr S=InitStack();
	Mark[1][1]=1;
	Pos a;
	a.x=1;a.y=1;
	Push(S,a);
	Path(1,1,S);
	return 0;
}