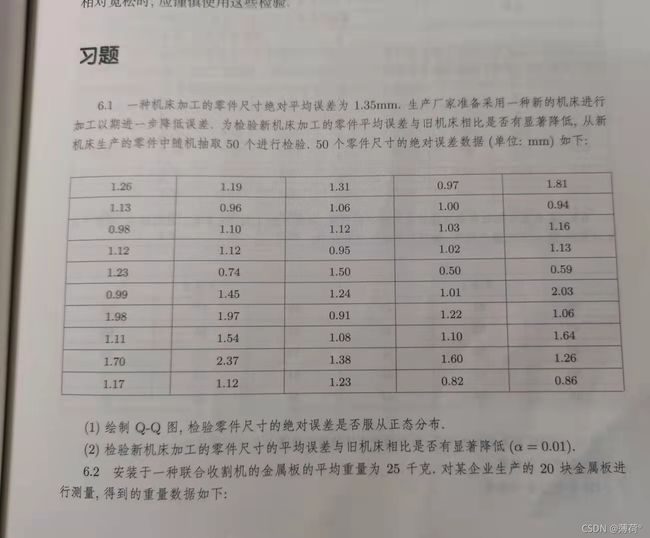
统计学-——基于R 第六章课后习题 假设检验
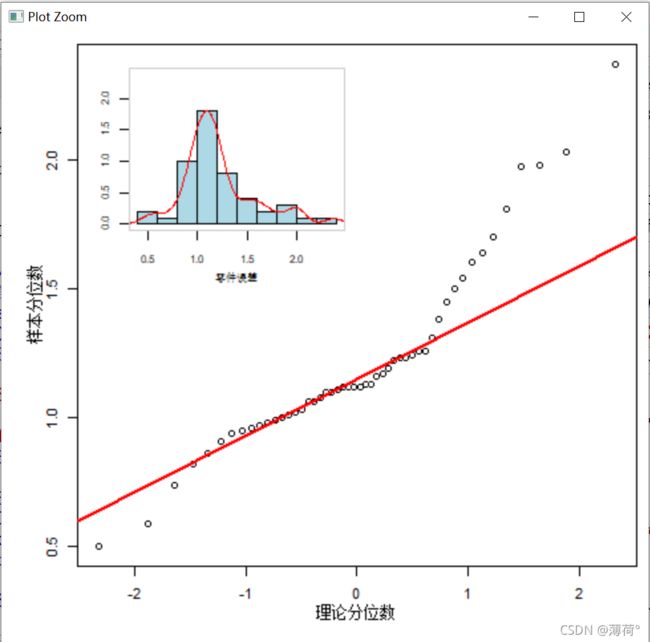
6.1(1)Q-Q图
> exercise6_1<-read.csv("D:/289250《统计学—基于R》(第4版)—例题和习题数据/《统计学—基于R》(第4版)—例题和习题数据(公开资源)/exercise/chap06/exercise6_1.csv") #导入exercise6_1文件
> par(mai=c(0.6,0.6,0.1,0.1),cex=0.7,mgp=c(2,1,0))
> qqnorm(exercise6_1$零件误差,xlab="理论分位数",ylab="样本分位数",main="") #绘制Q-Q点
> qqline(exercise6_1$零件误差,col="red",lwd=2) #添加Q-Q线
> par(fig=c(0.08,0.55,0.55,0.96),new=TRUE) #设置图形位置
> hist(exercise6_1$零件误差,xlab="零件误差",ylab="",ylim=c(0,2.37),freq=FALSE,col="lightblue",cex.axis=0.7,cex.lab=0.7,main="") #绘制直方图
> lines(density(exercise6_1$零件误差),col="red") #添加核密度曲线
> box(col="grey80") #添加盒子答:由图可知,各点并非在理论正态分布直线周围随机分布,且观测值越大或越小,越偏离理论正态分布,所以零件尺寸的绝对误差不服从正态分布
(2)一个总体均值的检验(大样本)
假设H0>=1.35;H1<1.35
> library(lattice)
> library(BSDA)
> z.test(exercise6_1$零件误差,mu=1.35,sigma.x=sd(exercise6_1$零件误差),alternative="less",conf.level=0.99)
One-sample z-Test
data: exercise6_1$零件误差
z = -2.6061, p-value = 0.004579
alternative hypothesis: true mean is less than 1.35
99 percent confidence interval:
NA 1.33553
sample estimates:
mean of x
1.2152
答:平均数=1.2152,z=-2.6061, P = 0.004579,P<0.05,拒绝H0,有证据显示新机床加工零件尺寸的平均误差与旧机床相比有显著降低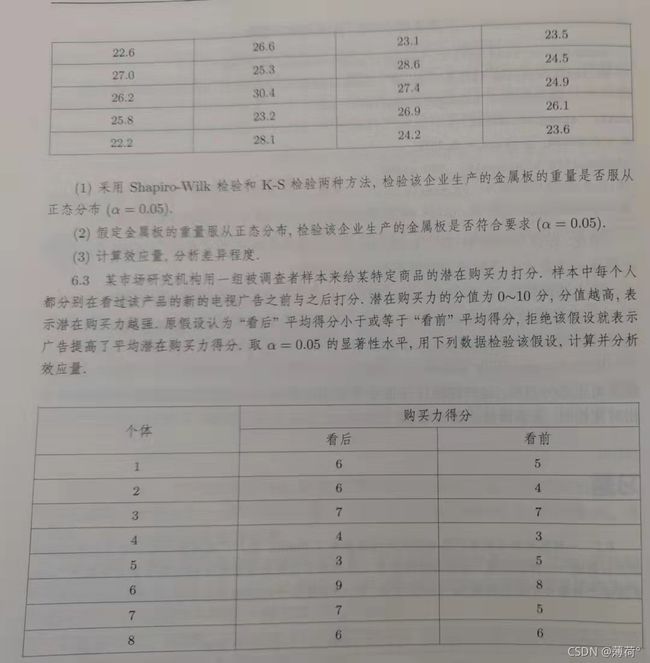
6.2
(1)
H0:服从正态分布
H1:不服从正态分布
Shapiro-Wilk正态性检验
> exercise6_2<-read.csv("D:/289250《统计学—基于R》(第4版)—例题和习题数据/《统计学—基于R》(第4版)—例题和习题数据(公开资源)/exercise/chap06/exercise6_2.csv")
> shapiro.test(exercise6_2$重量)
Shapiro-Wilk normality test
data: exercise6_2$重量
W = 0.97064, p-value = 0.7684答:W = 0.97064, P = 0.7684,P>0.05,不拒绝原假设,没有证据显示该企业生产的金属板的重量服从正态分布
K-S正态性检验
> ks.test(exercise6_2$重量,"pnorm",mean(exercise6_2$重量),sd(exercise6_2$重量))
One-sample Kolmogorov-Smirnov test
data: exercise6_2$重量
D = 0.10808, p-value = 0.9539
alternative hypothesis: two-sided答:D = 0.10808, P = 0.9539,P>0.05,不拒绝原假设,没有证据显示该企业生产的金属板的重量服从正态分布
(2)H0:μ=25;H1:μ≠25
一个总体均值的检验(小样本)
> t.test(exercise6_2$重量,mu=25)
One Sample t-test
data: exercise6_2$重量
t = 1.0399, df = 19, p-value = 0.3114
alternative hypothesis: true mean is not equal to 25
95 percent confidence interval:
24.48352 26.53648
sample estimates:
mean of x
25.51 答:x=25.51,t = 1.0399, df = 19, P = 0.3114,由于P>0.05,不拒绝H0,没有证据显示该企业生产的金属板符合要求
(3)计算单样本t检验的效应量
> cohensD(exercise6_2$重量,mu=25)
[1]0.2325298答:平均重量与标准重量相差0.2325298个标准差,该结果属于中的效应量
6.3 配对样本t检验效应量
H0:μ1-μ2=0;H2:μ1-μ2≠0
> exercise6_3<-read.csv("D:/289250《统计学—基于R》(第4版)—例题和习题数据/《统计学—基于R》(第4版)—例题和习题数据(公开资源)/exercise/chap06/exercise6_3.csv")
> library(lsr)
> cohensD(exercise6_3$看前,exercise6_3$看后,method="paired")
[1] 0.4798574答:结果显示,d=0.4798574,根据Cohen准则,该检验结果属于中的效应量
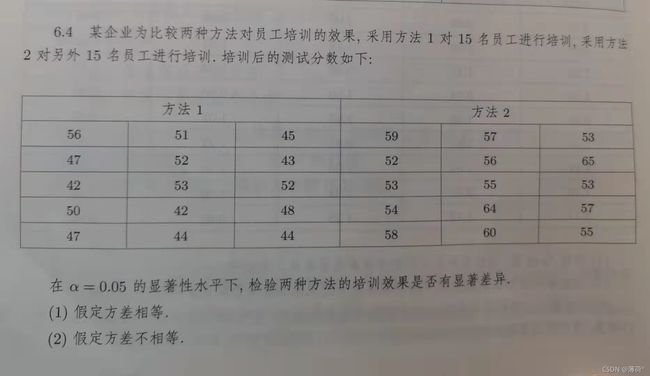
6.5
(1)两个总体均值之差的检验(独立小样本)
H0:μ1-μ2=0;H2:μ1-μ2≠0
> exercise6_4<-read.csv("D:/289250《统计学—基于R》(第4版)—例题和习题数据/《统计学—基于R》(第4版)—例题和习题数据(公开资源)/exercise/chap06/exercise6_4.csv")
> #假设总体方差相等
> t.test(exercise6_4$方法1,exercise6_4$方法2,var.equal=TRUE)
Two Sample t-test
data: exercise6_4$方法1 and exercise6_4$方法2
t = -5.8927, df = 28, p-value = 2.444e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-12.128568 -5.871432
sample estimates:
mean of x mean of y
47.73333 56.73333
> #假设总体方差不相等
> t.test(exercise6_4$方法1,exercise6_4$方法2,var.equal=FALSE)
Welch Two Sample t-test
data: exercise6_4$方法1 and exercise6_4$方法2
t = -5.8927, df = 27.639, p-value = 2.568e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-12.130411 -5.869589
sample estimates:
mean of x mean of y
47.73333 56.73333 答:在该项检验中,x方法1=47.73333,x方法2=56.73333,假设总体方差相等时,t = -5.8927, df = 28, P = 2.444e-06;假设总体方差不等时,t = -5.8927, df = 27.639, P = 2.568e-06。两种假设条件下检验的P值均小于0.05,所以拒绝H0,两家培训效果有显著差异
(3)独立样本t检验的效应量
> library(lsr)
> cohensD(exercise6_4$方法1,exercise6_4$方法2)
[1] 2.151704答:结果显示,d=2.151704,表示方法1与方法2的培训效果相差2.151704个标准差,根据Cohen准则,该结果属于大的效应量
6.5 一个总体比例的检验
H0:<=17%;H1>17%
> n<-550
> p<-115/550
> pi0<-0.17
> z<-(p-pi0)/sqrt(pi0*(1-pi0)/n)
> p_value<-1-pnorm(z)
> data.frame(z,p_value)
z p_value
1 2.440583 0.007331785答:在该项检验中,z=2.440583 P=0.007331785,由于P<0.05,拒绝H0,因此生产商的说法属实
6.6 两个总体比例只差的检验
H0:π1-π2>=0;π1-π2<0
> n1<-100;n2<-95
> p1<-24/100;p2<-39/95
> p<-(p1*n1+p2*n2)/(n1+n2)
> z<-(p1-p2)/sqrt(p*(1-p)*(1/n1+1/n2))
> p_value<-pnorm(z)
> data.frame(z,p_value)
z p_value
1 -2.545149 0.00546155答:在此检验中,z=-2.545149 P=0.00546155,由于P<0.05,拒绝H0,即男女比例成功的人数有显著差异
6.7 两个总体均值之差的检验(配对样本)
(1)H0:μ1-μ2=0;H2:μ1-μ2≠0
> exercise6_7<-read.csv("D:/289250《统计学—基于R》(第4版)—例题和习题数据/《统计学—基于R》(第4版)—例题和习题数据(公开资源)/exercise/chap06/exercise6_7.csv")
> t.test(exercise6_7$旧肥料,exercise6_7$新肥料,var.equal=TRUE)
Two Sample t-test
data: exercise6_7$旧肥料 and exercise6_7$新肥料
t = -5.4271, df = 38, p-value = 3.474e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-12.631742 -5.768258
sample estimates:
mean of x mean of y
100.7 109.9 答:旧肥料=100.7 ,新肥料=109.9 ,总体方差相等时,t = -5.4271, df = 38, P = 3.474e-06,P<0.05,拒绝H0,新肥料显著高于旧肥料
(2)两个总体方差比的检验
> var.test(exercise6_7[,1],exercise6_7[,2],alternative="two.sided")
F test to compare two variances
data: exercise6_7[, 1] and exercise6_7[, 2]
F = 0.72294, num df = 19, denom df = 19, p-value
= 0.4862
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.2861488 1.8264749
sample estimates:
ratio of variances
0.722941 答:s1平方/s2平方=0.722941, F = 0.72294, df1 = 19, df2 = 19, P=0.4862,P>0.05,不拒绝H0,没有证据显示两种化肥有显著差异
(3)配对样本t检验的效应量
> cohensD(exercise6_7$旧肥料,exercise6_7$新肥料,method="paired")
[1] 1.044093答:结果显示d=1.044093,根据Cohen准则,该检验结果属于大的效应量
6.8
H0:无差异;H1:有差异
> exercise6_8<-read.csv("D:/289250《统计学—基于R》(第4版)—例题和习题数据/《统计学—基于R》(第4版)—例题和习题数据(公开资源)/exercise/chap06/exercise6_8.csv")
> var.test(exercise6_8[,1],exercise6_8[,2],alternative="two.sided")
F test to compare two variances
data: exercise6_8[, 1] and exercise6_8[, 2]
F = 9.0711, num df = 23, denom df = 23, p-value =
1.477e-06
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
3.924078 20.969026
sample estimates:
ratio of variances
9.071058
答:P=1.477e-06,P<0.05,拒绝H0,两部机器生产的袋茶重量的方差存在差异