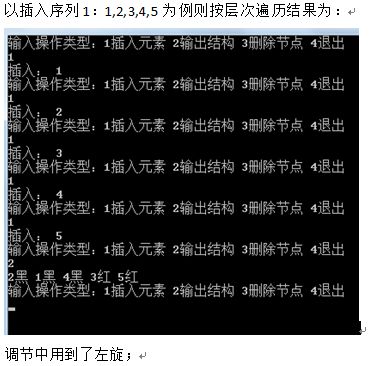
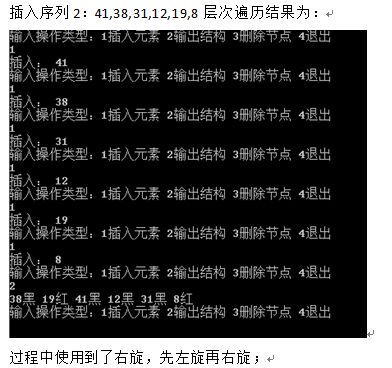
rbtree插入算法分析
#include<iostream>
#include<queue>
using namespace std;
struct rbnode{
int key;
int color;//1=black,0=red;
struct rbnode *p,*left,*right;
rbnode(){}
rbnode(int k){key=k;
}
};
rbnode *nil;
bool RBinsert(rbnode **root,int k);
void LevelOrder(rbnode *t);
void RBinserFix(rbnode **root,rbnode *z);
void Left(rbnode **root, rbnode *x);
void Right(rbnode **root, rbnode *x);
void Left(rbnode **root, rbnode *x){
if(x->right!=nil){
rbnode * y=nil;
y=x->right;
x->right=y->left;
if(y->left!=nil)y->left->p=x;
y->p=x->p;
if(x->p==nil) (*root)=y;
else if(x==x->p->left) x->p->left=y;
else x->p->right=y;
y->left=x;
x->p=y;}
}
void Right(rbnode **root, rbnode *x){
if(x->left!=nil){
rbnode * y=nil;
y=x->left;
x->left=y->right;
if(y->right!=nil)y->right->p=x;
y->p=x->p;
if(x->p==nil) (*root)=y;
else if(x==x->p->right) x->p->right=y;
else x->p->left=y;
y->right=x;
x->p=y;
}
}
void RBinserFix(rbnode **root,rbnode *z){
rbnode* y=nil;
while(z!=*root&&z->p->color==0){
if(z->p==z->p->p->left){
y=z->p->p->right;
if(y->color==0){
z->p->color=1;
y->color=1;
z->p->p->color=0;
z=z->p->p;
}else
{ if(z==z->p->right){z=z->p;//LEFT
Left(root,z);}
z->p->color=1;
z->p->p->color=0;
//RightRotate();
Right((root),z->p->p);
}
}else {
y=z->p->p->left;
if(y->color==0){
z->p->color=1;
y->color=1;
z->p->p->color=0;
z=z->p->p;
}else
{ if(z==z->p->left){z=z->p;//LEFT
Right(root,z);
}
z->p->color=1;
z->p->p->color=0;
//RightRotate();
Left((root),z->p->p);}
}
}
(*root)->color=1;
}
bool RBinsert(rbnode **root,int k){
rbnode* z=new rbnode(k);
//cout<<root->color;
rbnode* y=nil;
rbnode* x=*root;
while(x!=nil){
y=x;
if(k==x->key)return 0;
if(k<x->key)x=x->left;
else x=x->right;
}
z->p=y;
if(y==nil) {(*root)=z;(*root)->p=nil;}
else if(k<y->key) y->left=z;
else y->right=z;
z->left=nil;z->right=nil;
z->color=0;
//LevelOrder(*root);
RBinserFix(root,z);
return 1;
}
void Visit(rbnode *t) {
if (t) {
cout << t->key;
if(t->color)cout<<"黑 ";
else cout<<"红 ";
}
}
void LevelOrder(rbnode *t) {// 对* t逐层遍历
queue<rbnode*> Q;
while (t!=nil) {
Visit(t);
if (t->left!=nil)
Q.push(t->left);
if (t->right!=nil)
Q.push(t->right);
if (Q.empty())
break;
t=Q.front();
Q.pop();
}
}
void main(){
//rbnode* root=
//root->color=1;//1=black
//root->p=nil;
//root->left=nil;root->right=nil;
rbnode** root=(rbnode**)malloc(sizeof(rbnode*));;
nil=new rbnode();
nil->color=1;
*root =nil;
//rbnode
cout<<"输入操作类型:1插入元素 2输出结构 3删除节点 4退出"<<endl;
int sinin,num;
cin>>sinin;
while(sinin!=4)
{switch(sinin){
case 1:
cout<<"插入: ";
cin>>num;
if(!RBinsert(root,num))cout<<"插入重复值"<<endl;
// cout<<" root --key:"<<(*root)->p->color<<endl;
break;
case 2:
LevelOrder(*root);
cout<<endl;
break;
case 3:
break;
}cout<<"输入操作类型:1插入元素 2输出结构 3删除节点 4退出"<<endl;
cin>>sinin;
}
}
红黑树每个节点由5个域组成:parent,leftchild,rightchild,key,color组成
插入过程分为两大部分,即1)插入到树中2)维持红黑树性质
1)根据节点key值,插入时P节点的左子树均小于该节点key值,右子树各节点均大于p节点的key值,根据这个特征,如果小于p的key就到p的左子树寻找,否则到p的右子树。
2)在插入一个节点到树中后,会引起不满足红黑树定义的变化,需要进行调节。调节方法有三种:1、调节颜色,2、左旋,3、右旋。不满足红黑树条件的原因是,插入时父节点为红色(或为根)。下图展示针对各种情况的旋转调节方法:
注:调节时先采用调节颜色的方法,且最对经过2次旋转达到平衡。
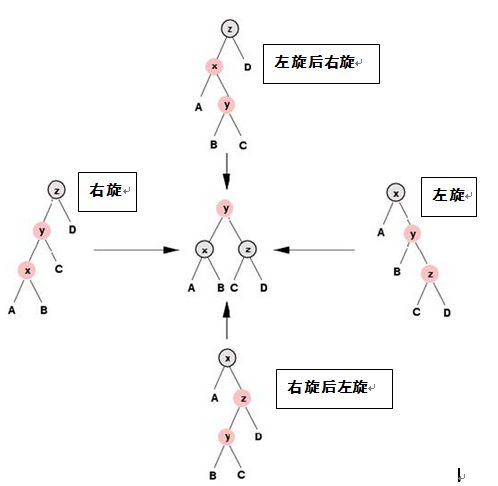
旋转过程中,二叉搜索树的性质保持不变
插入过程:小于节点值访问左子树,大于节点值访问右子树,否则返回插入失败O(logn)
调节过程:
void RBinserFix(T, z){
while(colorp[z] ==RED){
//若z为根,则p[z]=nil[T],颜色为黑,不进入循环,p[z]为黑也不进入
if(p[z] == left[p[p[z]]]){//z的父节点是祖父节点的左孩子
y= right[p[p[z]]];//y是z的叔叔,若为红色则调节颜色
if(color[y] ==RED){//改变颜色,case1
color[p[z]] =BLACK;
color[y]=BLACK;
color[p[p[z]]=RED;
z=p[p[z]];
}else //case2,3
{ if(z==right[p[z]]){//case 2,左旋
z=p[z]; Left(root,z);
}
Color[p[z]]=BLACK;//case3,右旋
Color[p[p[z]]]=RED;
Right((root),p[p[z]]);//p[z]为黑,退出
}
}else {//对调上方“左”“右”, z的父节点是祖父节点的右孩子}
}//endwhile
Color[root[t]]=BLACK;
}
复杂程度为O(logn)
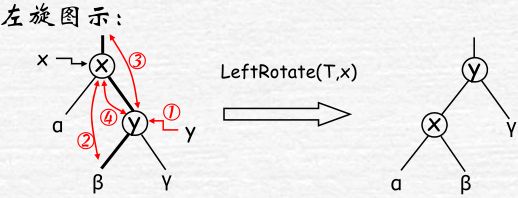
Left(T,x)
{//假设right[x]!=nil[T]
Y=right[x] //记录指向y节点的指针,1
right[x]=left[y];p[left[y]]=x;// B连到X右,2
p[y]=p[x ];//修改parent指针,3
if(p[x]=nil[T]) //x是根
root[T]=y; //修改树指针
else if (x==left[p[x]]) left[p[x]]=y; //修改父节点孩子指针
else right[p[x]]=y;
left[y]=x; p[x]=y;//x连接到y,4
}
复杂程度为O(1)
整个插入算法的时间是O(logn)