ISTA 算法
ISTA 算法
文章目录
- ISTA 算法
-
- 1、引言
- 2、迭代收缩阈值算法(ISTA)
1、引言
对于一个基本的线性逆问题:
y = A x + w \mathbf{y}=\mathbf{A}\mathbf{x}+\mathbf{w} y=Ax+w
其中 A ∈ M × N \mathbf{A} \in M \times N A∈M×N, y ∈ M \mathbf{y} \in M y∈M 且是已知的, w \mathbf{w} w 是未知噪声。
(1) 式可用最小二乘法(Least Squares)来求解:
x ^ L S = arg mi x n ∥ A x − y ∥ 2 2 \hat{\mathbf{x}}_{L S}=\underset{\mathbf{x}}{\arg \operatorname{mi}} n\|\mathbf{A x}-\mathbf{y}\|_{2}^{2} x^LS=xargmin∥Ax−y∥22
当 M = N M=N M=N 且 A \mathbf{A} A 非奇异时,最小二乘法的解等价于 A − 1 y \mathbf{A}^{-1}\mathbf{y} A−1y。
然而,在很多情况下, A \mathbf{A} A 是病态的(ill-conditioned),此时,用最小二乘法求解时,系统微小的扰动都会导致结果差别很大,可谓失之毫厘谬以千里,因此最小二乘法不适用于求解病态方程。
**什么是条件数?**矩阵 A \mathbf{A} A 的条件数是指 A \mathbf{A} A 的最大奇异值与最小奇异值的比值,显然条件数最小为 1,条件数越小说明矩阵越趋于 “良态”,条件数越大,矩阵越趋于奇异,从而趋于 “病态”。
为了求解病态线性系统的逆问题,前苏联科学家安德烈·尼古拉耶维奇·吉洪诺夫提出了吉洪诺夫正则化方法(Tikhonov regularization),该方法也称为 “岭回归”。最小二乘是一种无偏估计方法(保真度很好),如果系统是病态的,则会导致其估计方差很大(对扰动很敏感),吉洪诺夫正则化方法的主要思想是以可容忍的微小偏差来换取估计的良好效果,实现方差和偏差的一个 trade-off(权衡)。吉洪诺夫正则化求解病态问题可以表示为:
x ^ T = arg min x ∥ A x − y ∥ 2 2 + λ ∥ x ∥ 2 2 \hat{\mathbf{x}}_{T}=\underset{\mathbf{x}}{\arg \operatorname{min}} \|\mathbf{A x}-\mathbf{y}\|_{2}^{2} + \lambda \|\mathbf{x}\|_{2}^{2} x^T=xargmin∥Ax−y∥22+λ∥x∥22
其中 λ > 0 \lambda > 0 λ>0 为正则化参数。问题 (3) 的解等价于如下岭回归估计器:
x ^ T = ( x T x + λ I ) − 1 x T y \hat{\mathbf{x}}_{T}=(\mathbf{x^T}\mathbf{x}+\lambda \mathbf{I})^{-1}\mathbf{x^T}\mathbf{y} x^T=(xTx+λI)−1xTy
岭回归是采用 ℓ 2 ℓ2 ℓ2 范数作为正则项,另一种求解式 (1) 的方法是采用 ℓ 1 ℓ1 ℓ1 范数作为正则项,这就是经典的 LASSO(Least absolute shrinkage and selection operator)问题:
x ^ = arg min x ∥ A x − y ∥ 2 2 + λ ∥ x ∥ 1 \hat{\mathbf{x}}=\underset{\mathbf{x}}{\arg \operatorname{min}} \|\mathbf{A x}-\mathbf{y}\|_{2}^{2} + \lambda \|\mathbf{x}\|_{1} x^=xargmin∥Ax−y∥22+λ∥x∥1
采用 ℓ 1 ℓ1 ℓ1 范数正则项相对于 ℓ 2 ℓ2 ℓ2 范数正则项有两个优势:
- 第一个优势是 ℓ 1 ℓ1 ℓ1 范数正则项能产生稀疏解,
- 第二个优势是其具有对异常值不敏感的特性,这一点恰好与岭回归相反。
式 (5) 中的问题是一个凸优化问题,通常可以转化为二阶锥规划(second order cone programming)问题,从而使用内点法(interior point)等方法求解。然而在大规模问题中,由于数据维度太大,而内点法的算法复杂度为 O ( N 3 ) O(N^3) O(N3),导致求解非常耗时。
基于上述原因,很多研究者研究通过简单的**基于梯度的方法**来求解(5)式。基于梯度的方法其计算量主要集中在矩阵 A \mathbf{A} A 与向量 y \mathbf{y} y 的乘积上,算法复杂度小,而且算法结构简单,容易操作。
2、迭代收缩阈值算法(ISTA)
在众多基于梯度的算法中,迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm)是一种非常受关注的算法,ISTA 算法在每一次迭代中通过一个收缩/软阈值操作来更新 x \mathbf{x} x,其具体迭代格式如下:
x k + 1 = soft λ t ( x k − 2 t A T ( A x k − y ) ) \mathbf{x}_{k+1}=\operatorname{soft}_{\lambda t}\left(\mathbf{x}_{k}-2 t \mathbf{A}^{\mathrm{T}}\left(\mathbf{A} \mathbf{x}_{k}-\mathbf{y}\right)\right) xk+1=softλt(xk−2tAT(Axk−y))
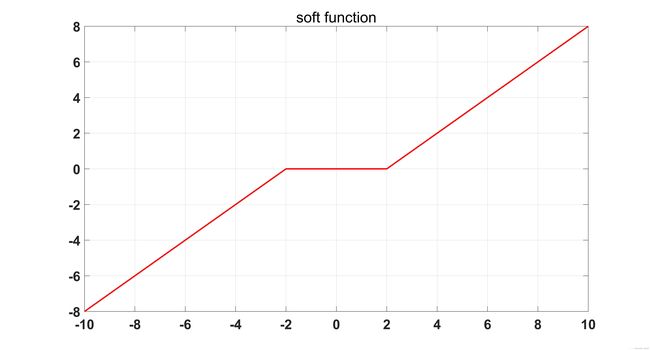
其中 soft λ t \operatorname{soft}_{\lambda t} softλt 是软阈值操作函数:
soft T ( x ) = sign ( x i ) ( ∣ x i ∣ − T ) \operatorname{soft}_{T}(\mathbf{x})=\operatorname{sign}(x_i)(|x_i|-T) softT(x)=sign(xi)(∣xi∣−T)
软阈值操作函数如下图所示,其中 sign ( ) \operatorname{sign}() sign() 是符号函数。:
那么 ISTA 的迭代格式(6)式是怎么来的呢?算法中的 “收缩阈值” 体现在哪里?这要从梯度下降法(Gradient Descent)说起。
考虑一个连续可导的无约束最小化问题:
min { f ( x ) : x ∈ R N } \operatorname{min}\{f(\mathbf{x}):\mathbf{x} \in R^N\} min{f(x):x∈RN}
(8) 式可用梯度下降法来求解:
x 0 ∈ R N ; x k = x k − 1 − t k ∇ f ( x k − 1 ) \mathbf{x}_0 \in R^N; \mathbf{x}_k=\mathbf{x}_{k-1}-t_k\nabla f(\mathbf{x}_{k-1}) x0∈RN;xk=xk−1−tk∇f(xk−1)
这里 t k > 0 t_k > 0 tk>0 是迭代步长。我们知道,梯度下降法可以表示成 f 在点 x k − 1 \mathbf{x}_{k-1} xk−1 处的近端正则化(proximal regularization),其等价形式可以表示为:
x k = arg min x { f ( x k − 1 ) + ⟨ x − x k − 1 , ∇ f ( x k − 1 ) ⟩ + 1 2 t k ∥ x − x k − 1 ∥ 2 2 } \mathbf{x}_{k}=\underset{\mathbf{x}}{\arg \min }\left\{f\left(\mathbf{x}_{k-1}\right)+\left\langle\mathbf{x}-\mathbf{x}_{k-1}, \nabla f\left(\mathbf{x}_{k-1}\right)\right\rangle+\frac{1}{2 t_{k}}\left\|\mathbf{x}-\mathbf{x}_{k-1}\right\|_{2}^{2}\right\} xk=xargmin{f(xk−1)+⟨x−xk−1,∇f(xk−1)⟩+2tk1∥x−xk−1∥22}
(9)-(10)可由李普希兹连续条件 ∥ ∇ f ( x k ) − ∇ f ( x k − 1 ) ∥ 2 ≤ L ( f ) ∥ x k − x k − 1 ∥ 2 \left\|\nabla f\left(\mathbf{x}_{k}\right)-\nabla f\left(\mathbf{x}_{k-1}\right)\right\|_{2} \leq L(f)\left\|\mathbf{x}_{k}-\mathbf{x}_{k-1}\right\|_{2} ∥∇f(xk)−∇f(xk−1)∥2≤L(f)∥xk−xk−1∥2 和 f 在 x k − 1 x_{k-1} xk−1 处的 2 阶泰勒展开得到
将 (8) 式加上 ℓ 1 ℓ1 ℓ1 范数正则项,得到:
min { f ( x ) + λ ∥ x ∥ 1 ) : x ∈ R N } \operatorname{min}\{f(\mathbf{x}) + \lambda \|\mathbf{x}\|_1):\mathbf{x} \in R^N\} min{f(x)+λ∥x∥1):x∈RN}
则 (10) 式相应变成:
x k = arg min x { f ( x k − 1 ) + ⟨ x − x k − 1 , ∇ f ( x k − 1 ) ⟩ + 1 2 t k ∥ x − x k − 1 ∥ 2 2 + λ ∥ x ∥ 1 } \mathbf{x}_{k}=\underset{\mathbf{x}}{\arg \min }\left\{f\left(\mathbf{x}_{k-1}\right)+\left\langle\mathbf{x}-\mathbf{x}_{k-1}, \nabla f\left(\mathbf{x}_{k-1}\right)\right\rangle+\frac{1}{2 t_{k}}\left\|\mathbf{x}-\mathbf{x}_{k-1}\right\|_{2}^{2}+ \lambda\|\mathbf{x}\|_1\right\} xk=xargmin{f(xk−1)+⟨x−xk−1,∇f(xk−1)⟩+2tk1∥x−xk−1∥22+λ∥x∥1}
(12) 忽略掉常数项 f ( x k − 1 ) f(\mathbf{x}_{k-1}) f(xk−1) 和 ∇ f ( x k − 1 ) \nabla f(\mathbf{x}_{k-1}) ∇f(xk−1) 之后,(12) 式可以写成:
x k = soft λ t k ( x k − 1 − t k ∇ f ( x k − 1 ) ) \mathbf{x}_{k}=\operatorname{soft}_{\lambda t_k}(\mathbf{x}_{k-1}-t_k \nabla f(\mathbf{x}_{k-1})) xk=softλtk(xk−1−tk∇f(xk−1))
文献中已经证明,当迭代步长取 f 的李普希兹常数的倒数(即 1 L ( f ) \frac{1}{L(f)} L(f)1)时,由 ISTA 算法生成的序列 x k \mathbf{x}_k xk 的收敛速度为 O ( 1 N ) O(\frac{1}{N}) O(N1) ,显然为次线性收敛速度。
function [x_hat,error] = cs_ista(y,A,lambda,epsilon,itermax)
% Iterative Soft Thresholding Algorithm(ISTA)
% Version: 1.0 written by Louis Zhang @2019-12-7
% Reference: Beck, Amir, and Marc Teboulle. "A fast iterative
% shrinkage-thresholding algorithm for linear inverse problems."
% SIAM journal on imaging sciences 2.1 (2009): 183-202.
% Inputs:
% y - measurement vector
% A - measurement matrix
% lambda - denoiser parameter in the noisy case
% epsilon - error threshold
% inter_max - maximum number of amp iterations
%
% Outputs:
% x_hat - the last estimate
% error - reconstruction error
if nargin < 5
itermax = 10000 ;
end
if nargin < 4
epsilon = 1e-4 ;
end
if nargin < 3
lambda = 2e-5 ;
end
N = size(A,2) ;
error = [];
x_1 = zeros(N,1) ;
for i = 1:itermax
g_1 = A'*(y - A*x_1) ;
alpha = 1 ;
% obtain step size alpha by line search
% alpha = (g_1'*g_1)/((A*g_1)'*(A*g_1)) ;
x_2 = x_1 + alpha * g_1 ;
x_hat = sign(x_2).*max(abs(x_2)-alpha*lambda,0) ;
error(i,1) = norm(x_hat - x_1) / norm(x_hat) ;
error(i,2) = norm(y-A*x_hat) ;
if error(i,1) < epsilon || error(i,1) < epsilon
break;
else
x_1 = x_hat ;
end
end