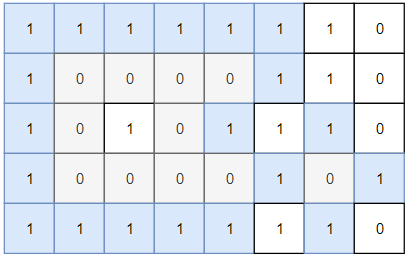
岛屿问题(用DFS遍历二维数组)
一文秒杀所有岛屿题目 :: labuladong的算法小抄 (gitee.io)
200. 岛屿数量 - 力扣(LeetCode)
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
思路:
用DFS算法/BFS算法遍历二维数组,将二维矩阵中的每一个位置看做一个节点,这个节点的上下左右四个位置就是相邻节点,那么整个矩阵就可以抽象成一幅网状的图结构。因为是遍历一幅图,所以遍历的过程中还需要一个 visited 布尔数组防止走回头路。
这道题中没有使用visited数组,而是选择每次遇到岛屿时,都用DFS算法把岛屿淹掉,避免了维护visited数组。
class Solution {
public:
int numIslands(vector>& grid) {
int res=0;
for(int i=0;i>& grid)
{
int m=grid.size();
int n=grid[0].size();
//处理越界
if(i<0||i>=m||j<0||j>=n)
{
return ;
}
if(grid[i][j]=='0')//已经是海水了
{
return ;
}
grid[i][j]='0';//把grid[i][j]淹掉
//把grid[i][j]的上下左右都淹掉
dfs(i-1,j,grid);
dfs(i+1,j,grid);
dfs(i,j-1,grid);
dfs(i,j+1,grid);
}
}; 1254. 统计封闭岛屿的数目
二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。
请返回 封闭岛屿 的数目。
示例 1:
输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] 输出:2 解释: 灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
思路:
由题意得,靠边的陆地不算封闭岛屿,所以先用dfs把四条边上的陆地都排除掉,剩下的就是封闭岛屿。
class Solution {
public:
int closedIsland(vector>& grid) {
int m=grid.size();
int n=grid[0].size();
int res=0;
//把边上的岛都淹掉
for(int i=0;i>& grid,int i,int j)
{
int m=grid.size();
int n=grid[0].size();
//处理越界
if(i<0||j<0||i>=m||j>=n)
{
return ;
}
//已经是海水了
if(grid[i][j]==1)
{
return ;
}
//把grid[i][j]淹掉
grid[i][j]=1;
//把grid[i][j]的上下左右都淹掉
dfs(grid,i+1,j);
dfs(grid,i-1,j);
dfs(grid,i,j+1);
dfs(grid,i,j-1);
}
}; 695. 岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 思路: 给dfs设置返回值,记录每次淹没的陆地的面积
class Solution {
public:
int maxAreaOfIsland(vector>& grid) {
int res=0;
int m=grid.size();
int n=grid[0].size();
for(int i=0;i>& grid,int i,int j)
{
int m=grid.size();
int n=grid[0].size();
if(i<0||j<0||i>=m||j>=n)
{
return 0;
}
if(grid[i][j]==0)
{
return 0;
}
grid[i][j]=0;
return dfs(grid,i+1,j)
+dfs(grid,i-1,j)
+dfs(grid,i,j+1)
+dfs(grid,i,j-1)+1;
}
}; 1905. 统计子岛屿 - 力扣(LeetCode)
给你两个 m x n 的二进制矩阵 grid1 和 grid2 ,它们只包含 0 (表示水域)和 1 (表示陆地)。一个 岛屿 是由 四个方向 (水平或者竖直)上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。
如果 grid2 的一个岛屿,被 grid1 的一个岛屿 完全 包含,也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含,那么我们称 grid2 中的这个岛屿为 子岛屿 。
请你返回 grid2 中 子岛屿 的 数目 。
示例 1:
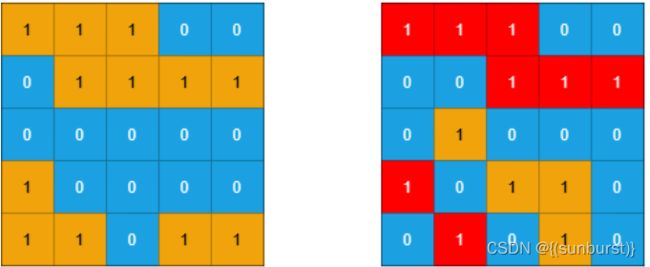
输入:grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出:3
解释:如上图所示,左边为 grid1 ,右边为 grid2 。
grid2 中标红的 1 区域是子岛屿,总共有 3 个子岛屿。
思路:
如果岛屿2中存在一片陆地,在岛屿1的对应位置是海水,那么岛屿2就不是岛屿1的子岛 ,
排除2中肯定不是子岛的岛屿
现在2中剩下的肯定都是子岛,就可以计算子岛数量了
class Solution {
public:
int countSubIslands(vector>& grid1, vector>& grid2) {
int m=grid2.size();
int n=grid2[0].size();
//如果岛屿2中存在一片陆地,在岛屿1的对应位置是海水,那么岛屿2就不是岛屿1的子岛
for(int i=0;i>& grid2,int i,int j)
{
int m=grid2.size();
int n=grid2[0].size();
if(i<0||j<0||i>=m||j>=n)
{
return ;
}
if(grid2[i][j]==0)
{
return ;
}
grid2[i][j]=0;
dfs(grid2,i+1,j);
dfs(grid2,i-1,j);
dfs(grid2,i,j+1);
dfs(grid2,i,j-1);
}
}; 827. 最大人工岛
给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。
返回执行此操作后,grid 中最大的岛屿面积是多少?
岛屿 由一组上、下、左、右四个方向相连的 1 形成。
示例 1:
输入: grid = [[1, 0], [0, 1]] 输出: 3 解释: 将一格0变成1,最终连通两个小岛得到面积为 3 的岛屿。
示例 2:
输入: grid = [[1, 1], [1, 0]] 输出: 4 解释: 将一格0变成1,岛屿的面积扩大为 4。
示例 3:
输入: grid = [[1, 1], [1, 1]] 输出: 4 解释: 没有0可以让我们变成1,面积依然为 4。
思路:
-
首先dfs找岛屿,找到一块就淹了它,并且给这个岛屿标记一下,存入HashMap(Key:岛屿的序号,Value,岛屿的面积)。给第一块岛屿标记为flag = -1,同时,在找的过程中,把访问到的格子的值改成flag。然后每当找到一块,flag--。有两个好处,第一,每块岛屿都被唯一标记了。第二,因为格子的值改成了小于0的flag,判断格子的值是否<=0就等效于visited数组的功能,使得回溯的过程中不会再访问已经访问过的格子。
-
对于已经标记完岛屿的地图,只需要挨个遍历,找到每个海洋(值为0)的格子,然后试一下上下左右是否可以连通,若联通,就计算一下联通之后的最大面积,更新答案。在这个过程中,需要用set判断上下左右有没有相同的岛屿,即每个岛屿只能加一次。
-
返回最大的答案
例:grid={ 遍历之后----》 grid={
{1,0,1}, {-1,0,-2},
{0,0,0}, {0,0,0},
{0,1,1} {0,-3,-3}
} }
unoedered_map
class Solution {
public:
int largestIsland(vector>& grid) {
unordered_map mapping;
int n=grid.size();
int flag=-1;//序号从-1开始递减,防止dfs时走回头路
for(int i=0;i s;
for(int i=0;i0) up=grid[i-1][j];
if(i0) left=grid[i][j-1];
if(j>& grid,int i,int j,int flag)
{
int n=grid.size();
if(i>=n||j>=n||i<0||j<0)//超出边界,返回0
return 0;
if(grid[i][j]<=0)//如果是海水或者其他已经被淹掉的陆地,那么就返回0
return 0;
if(grid[i][j]==1)//如果是陆地,就用flag把它淹掉(用flag标记它)
grid[i][j]=flag;
return dfs(grid,i+1,j,flag)+
dfs(grid,i-1,j,flag)+
dfs(grid,i,j+1,flag)+
dfs(grid,i,j-1,flag)+1;
}
}; 934. 最短的桥
给你一个大小为 n x n 的二元矩阵 grid ,其中 1 表示陆地,0 表示水域。
岛 是由四面相连的 1 形成的一个最大组,即不会与非组内的任何其他 1 相连。grid 中 恰好存在两座岛 。
你可以将任意数量的 0 变为 1 ,以使两座岛连接起来,变成 一座岛 。
返回必须翻转的 0 的最小数目。
示例 1:
输入:grid = [[0,1],[1,0]] 输出:1
示例 2:
输入:grid = [[0,1,0],[0,0,0],[0,0,1]] 输出:2
示例 3:
输入:grid = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]] 输出:1
思路:
最小翻转数 = 岛屿1 与 岛屿2 之间的最短路径
dfs(遍历二维数组) + bfs(找到最短路径)
如何找到最短路径?从一个岛屿开始,一圈一圈往外扩(BFS),直到扩展到第二座岛 。
遍历的思路类似于上题的最大人工岛,将遍历过的岛屿标记成“2”来做区分,而不是简单地淹掉。
class Solution {
public:
int shortestBridge(vector>& grid) {
vector> dire={{1,0},{0,1},{-1,0},{0,-1}};
queue> q;//队列中装的是各点的坐标
int n=grid.size();
int count=1;
for(int i=0;i0)
{
dfs(grid,q,i,j);
count--;
}
}
}
int step=0;
while(!q.empty())
{
int size=q.size();
for(int i=0;i=n||yn>=n)
{
continue;
}
if(grid[xn][yn]==0)//将周围的一圈海标记为2
{
grid[xn][yn]=2;
q.emplace(xn,yn);
}
if(grid[xn][yn]==1)//扩散中接触到了陆地,最短路径为step+1
return step+1;
}
}
step++;
}
return -1;
}
//深度优先遍历第一座岛,将岛屿及其周边的一圈都标记为 2
//将岛屿周边的一圈海的位置(i,j)压入队列中,做队列的初始化
void dfs(vector>& grid,queue>& q,int i,int j)
{
int n=grid.size();
if(i<0||j<0||i>=n||j>=n)
{
return ;
}
if(grid[i][j]==0)//岛屿周边的一圈海
{
grid[i][j]=2;//标记为 2
q.emplace(i,j);//将其位置(i,j)压入队列中
return ;
}
if(grid[i][j]==2)//遇到已经遍历过的,直接返回
return ;
grid[i][j]=2;//将遍历到的岛屿标记为 2
dfs(grid,q,i+1,j);
dfs(grid,q,i,j+1);
dfs(grid,q,i-1,j);
dfs(grid,q,i,j-1);
}
};