基于spss的多元统计分析 之 实例2（挤压塑料胶卷的最优工艺研究）（7/8）

主成分分析

摘要

主成分分析是利用降维的思想，把多指标转化为少数几个综合指标的多元统计分析方法。

对同一个个体进行多项观察时，必定涉及多个随机变量，它们都是相关的，一时难以综合。这时就需要进行主成分分析来概括诸多信息的主要方面，我们希望有一个或几个较好的综合分析来概括信息，而且希望综合指标相互独立地各代表某一方面的性质。任何一个度量指标的好坏除了可靠、真实之外，还必须能充分反应个体间的变异。如果有一项指标，个体间的取值都大同小异，那么该指标不能用来区分不同的个体。主成分分析是利用降维的思想，把多指标转化为少数几个综合指标的多元统计分析方法。

对同一个个体进行多项观察时，必定涉及多个随机变量，它们都是相关的，一时难以综合。这时就需要进行主成分分析来概括诸多信息的主要方面，我们希望有一个或几个较好的综合分析来概括信息，而且希望综合指标相互独立地各代表某一方面的性质。任何一个度量指标的好坏除了可靠、真实之外，还必须能充分反应个体间的变异。如果有一项指标，个体间的取值都大同小异，那么该指标不能用来区分不同的个体。

一、实验步骤

第五题：

1. 录入数据，先在spss中进行数据录入，如图：

   

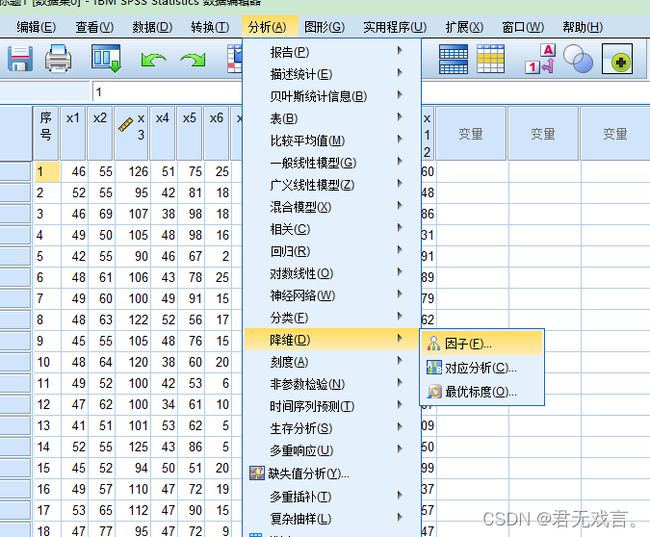
1.2 在spss里选择“分析”→“降维”→“因子””

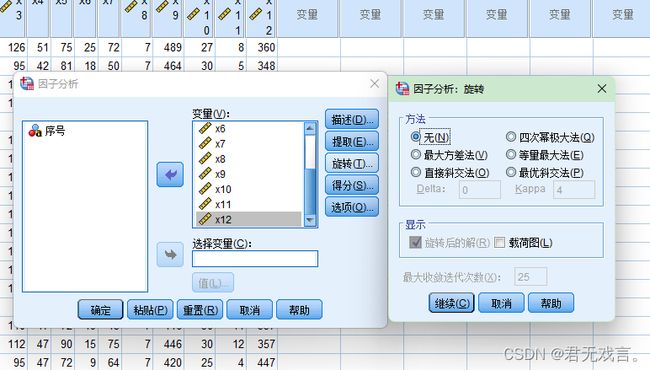
1.3将12个变量放入变量框，点击“描述”→“系数”→“继续”再点击“旋转”→“无”→“继续”→“确定”

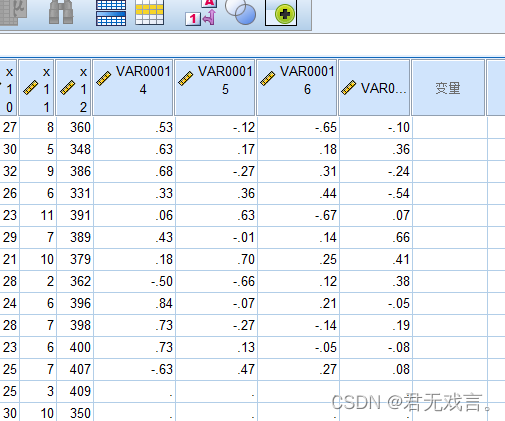
1.4将成分矩阵中的数据复制到数据视图中

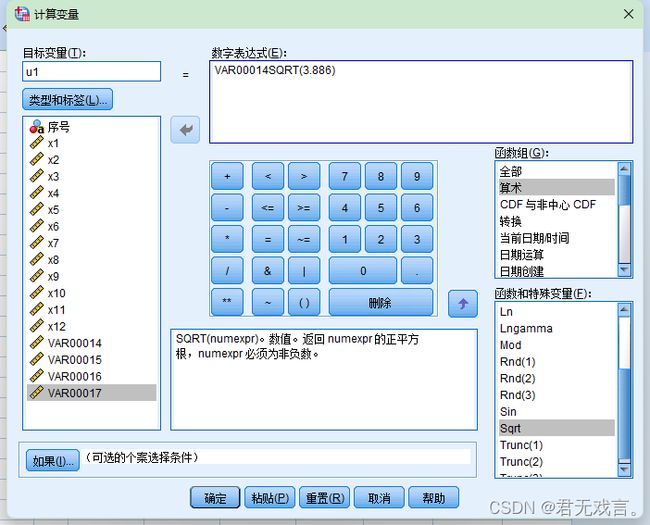
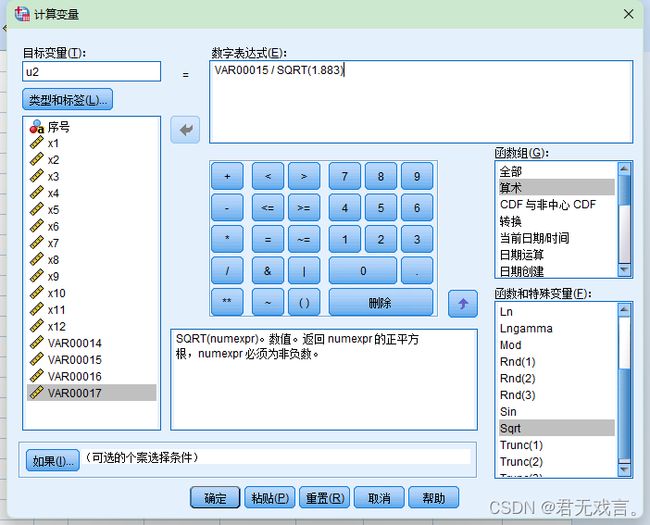
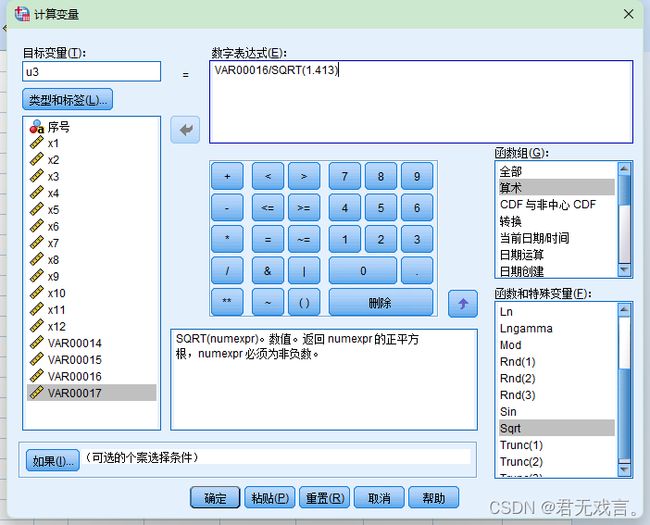
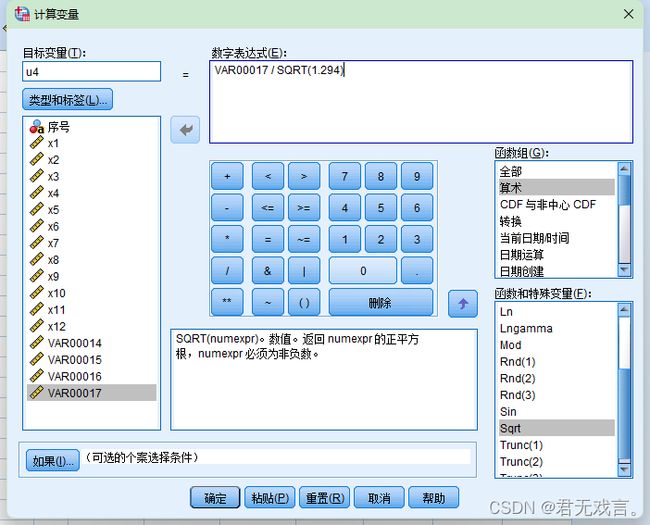
1.5点击“转换”→“计算变量”，在目标变量框分别输入u1，u2,u3,u4,在每次输入后分别在数字表达式框中输入VAR00014SQRT(3.886)，VAR00015 / SQRT(1.883)，VAR00016 / SQRT(1.413)，

VAR00017 / SQRT(1.294)，然后点击确定。

1.6点击“分析“→”描述统计“→”描述“，在描述对话框里将12个变量放入变量框中并勾选”将标准化值另存为变量（Z）“→”确定“

二、结果分析

第五题：

（KMO 和巴特利特检验图）

由KMO 和巴特利特检验，其p值小于0.05则表示拒绝原假设出错的概率小于0.05，那么选择拒绝原假设（变量之间没有相关性）。所以认为原始变量之间有较强的相关性。(主成分分析适用情况：适用于原有变量存在较高的相关程度)而KMO取样适切性量数，越接近1，数据可能得到的主成分分析模型越好。

公因子方差
	初始	提取
x1	1.000	.724
x2	1.000	.590
x3	1.000	.692
x4	1.000	.716
x5	1.000	.852
x6	1.000	.643
x7	1.000	.746
x8	1.000	.837
x9	1.000	.755
x10	1.000	.658
x11	1.000	.557
x12	1.000	.705
提取方法：主成分分析法。

提取列的数据表示为公共因子解释其余变量的方差的比例，即各变量含有原始变量的信息能被提取的公因子代表程度，可以看出说明提取的公因子对该变量的代表性是较强的

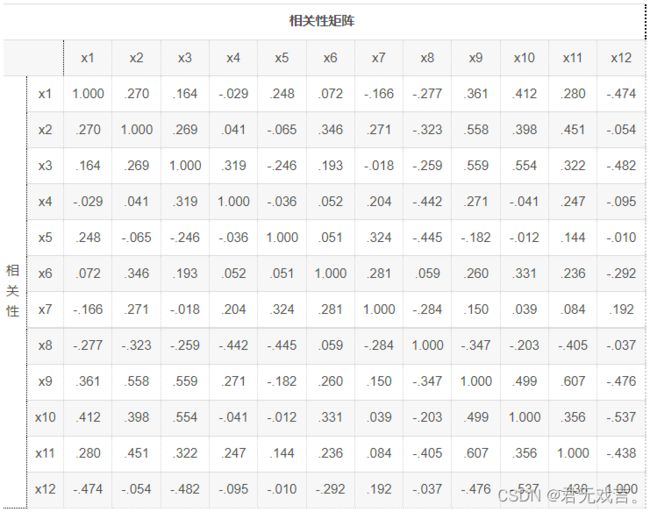
相关性矩阵，用于反应变量之间的相关程度，对于多重共线性，比如x9与x2和x3具有较高相关性但x2与x3也具有较高相关性，那么就可以说明该数据存在较为严重的多重共线性 （我们在回归分析中对多重共线性（相关程度很高）的变量解决方案一是去除一部分变量，二是用这些变量的线性组合。主成分分析就是利用第二种思想。）

总方差解释
成分	初始特征值			提取载荷平方和
	总计	方差百分比	累积 %	总计	方差百分比	累积 %
1	3.886	32.380	32.380	3.886	32.380	32.380
2	1.883	15.692	48.072	1.883	15.692	48.072
3	1.413	11.775	59.847	1.413	11.775	59.847
4	1.294	10.779	70.626	1.294	10.779	70.626
5	.950	7.915	78.542
6	.715	5.958	84.500
7	.556	4.630	89.130
8	.463	3.856	92.985
9	.295	2.454	95.440
10	.244	2.031	97.471
11	.180	1.502	98.973
12	.123	1.027	100.000
提取方法：主成分分析法。

显示提取的主成分，SPSS默认提取特征值大于1的主成分，本题提取了4个主成分其特征根分别为3.886，1.883，1.413，1.2942。其贡献率分别为32.380%,15.692%，11.775%，10.779%。累计贡献率不足80%,没有基本保留了原来指标的信息，假如其贡献率超过85%，这样就由原来的12指标转化为4个新指标，起到了降维的作用。（这也体现了主成分分析的基本思想：利用降维的思想，在损失很少信息的前提下，将多个指标转化为几个综合指标的方法。）

（碎石图）

碎石图则展示了每组的特征值，特征根的值越大说明其贡献率越大，可以用于证明自己总方差检验表的特征值是否造假。

成分矩阵a
	成分
	1	2	3	4
x1	.531	-.122	-.645	-.103
x2	.629	.173	.177	.364
x3	.682	-.265	.314	-.239
x4	.326	.356	.437	-.540
x5	.056	.634	-.665	.072
x6	.431	-.008	.142	.661
x7	.177	.697	.250	.408
x8	-.496	-.659	.117	.378
x9	.839	-.072	.208	-.050
x10	.728	-.268	-.140	.190
x11	.729	.130	-.052	-.078
x12	-.634	.474	.269	.075

成分矩阵表也称为因子载荷矩阵，主成分得分公式为f=w1*x1+w2*x2+…+wn*xn其中wi为主成分矩阵的值与该成分特征值（3.886，1.883，1.413，1.2942）。的开根值，代表权重。每个主成分矩阵（因子载荷矩阵）的值都要除以该成分特征值的开根值得到主成分公式的系数。然后通过实现步骤部分得到四个主成分的方程：

u1	u2	u3	u4
0.27	-0.09	-0.54	-0.09
0.32	0.13	0.15	0.32
0.35	-0.19	0.26	-0.21
0.17	0.26	0.37	-0.47
0.03	0.46	-0.56	0.06
0.22	-0.01	0.12	0.58
0.09	0.51	0.21	0.36
-0.25	-0.48	0.1	0.33
0.43	-0.05	0.17	-0.04
0.37	-0.2	-0.12	0.17
0.37	0.09	-0.04	-0.07
-0.32	0.35	0.23	0.07

主成分方程:

F1=0.27*x1+0.32*x2+0.35*x3+0.17*x4+0.03*x5+0.22*x6+0.09*x7-.25*x8+0.43*x9+0.37*x10+0.37*x11-0.32*x12

F2=-0.09*x1+0.13*x2-0.19*x3+0.26*x4+0.46*x5-0.01*x6+0.51*x7-0.48*x8-0.05*x9-0.2*x10+0.09*x11+0.35*x12

F3=-0.54*x1+0.15*x2+0.26*x3+0.37*x4-0.56*x5+0.12*x6+0.21*x7-0.1*x8+0.17*x9-0.12*x10-0.04*x11-0.23*x12

F4=-0.09*x1+0.32*x2-0.21*x3-0.47*x4+0.06*x5+0.58*x6+0.36*x7+0.33*x8-0.04x9-0.04*x10+0.17*x11-0.070.07*x12

最后通过每个主成分的贡献率得到综合得分：
F=0.3238*F1+0.15692*F2+0.11775*F3+0.10779*F4

(排序后的得分表)

三、讨论

引入：我们在回归分析种对多重共线性（相关程度很高）的变量解决方案一是去除一部分变量，二是用这些变量的线性组合。主成分分析就是利用第二种思想。实际问题中，多个变量具有一定相关关系，用较少的新变量代替原来较多的旧变量，而且使这些较少的新变量尽可能多地保留原来的变量，所反应的信息。

基本内容和作用：试图力保数据信息丢失最少的原则下，对这种多变量的数据表进行最佳综合简化。也就是对高维变量空间进行降维处理，使得在研究复杂问题时更容易抓主主要矛盾。

基本思想： 利用降维的思想，在损失很少信息的前提下，将多个指标转化为几个综合指标的方法。

适用情况：适用于原有变量存在较高的相关程度

性质：每个主成分的系数平方和为1，且主成分之间相互独立，且方差依次递减也就是重要性递减，并且主成分和原始变量的总方差相等。

方法简述：通过原始变量的相关矩阵或者协方差矩阵形成原始变量的线性组合从而产生几个综合指标（主成分）

贡献率：也就是第i个主成分的特征根（方差）在全部特征根（总方差）的比值。

主成分选取标准：累计贡献率达到85%

因子载荷量：也就是Xi（变量）与Fi（主成分）的相关系数

具体方法：从协方差矩阵计算

首先求样本均值和样本协方差矩阵，然后求特征方程解，得到特征根，利用特征根得到单位特征向量（a11 a21）最后得到特征向量矩阵（即满足向量元素的平方和为1）便可以得到主成分表达式也就是F1=a11（x1-x1的平均值）+a21（x2-x2的平均值）...即一个特征根的单位特征向量为主成分的系数。