LC-1595. 连通两组点的最小成本(状态压缩DP(记忆化搜索==>动态规划))
1595. 连通两组点的最小成本
难度困难86
给你两组点,其中第一组中有 size1 个点,第二组中有 size2 个点,且 size1 >= size2 。
任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出,其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。**如果两个组中的每个点都与另一组中的一个或多个点连接,则称这两组点是连通的。**换言之,第一组中的每个点必须至少与第二组中的一个点连接,且第二组中的每个点必须至少与第一组中的一个点连接。
返回连通两组点所需的最小成本。
示例 1:
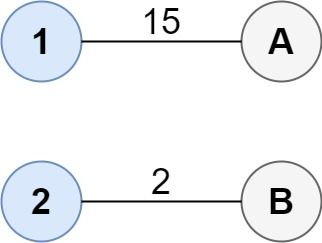
输入:cost = [[15, 96], [36, 2]]
输出:17
解释:连通两组点的最佳方法是:
1--A
2--B
总成本为 17 。
示例 2:
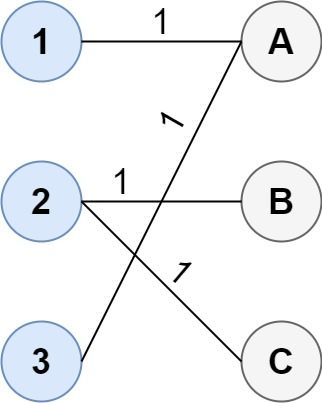
输入:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出:4
解释:连通两组点的最佳方法是:
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意,虽然有多个点连接到第一组中的点 2 和第二组中的点 A ,但由于题目并不限制连接点的数目,所以只需要关心最低总成本。
示例 3:
输入:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出:10
提示:
size1 == cost.lengthsize2 == cost[i].length1 <= size1, size2 <= 12size1 >= size20 <= cost[i][j] <= 100
状压DP(记忆化搜索 ==> 动态规划)
https://leetcode.cn/problems/minimum-cost-to-connect-two-groups-of-points/solution/jiao-ni-yi-bu-bu-si-kao-dong-tai-gui-hua-djxq/
class Solution {
int n, m;
int[][] cache;
List<List<Integer>> cost;
public int connectTwoGroups(List<List<Integer>> cost) {
this.cost = cost;
n = cost.size(); m = cost.get(0).size();
cache = new int[n][1 << m];
for(int i = 0; i < n; i++)
Arrays.fill(cache[i], -1);
return dfs(n-1, 0);
}
// 定义dfs(i, mask) 表示 在第一组中还有0-i个点需要连接,连接的第二组点在集合mask中,所需要的最小成本
// 转移:枚举第一组第i个点连接第二组中的任意一个点
// 递归边界: dfs(0, mask) ,此时mask中还为0的点可以连接任意第一组的点,选最小的成本
// 递归入口: dfs(全集,0)
public int dfs(int i, int mask){
if(i < 0){
if(mask == (1 << m) - 1)
return 0; // 第二组的点都选过了,没有额外成本
int ans = 0; // 寻找第二组中不为1的点,可以连接第一组任意点,选成本最小的点
for(int j = 0; j < m; j++){
if(((mask >> j) & 1) == 1) continue;
int min = Integer.MAX_VALUE;
for(int k = 0; k < n; k++){
min = Math.min(min, cost.get(k).get(j));
}
ans += min;
}
return ans;
}
if(cache[i][mask] >= 0) return cache[i][mask];
int ans = Integer.MAX_VALUE;
// 枚举第i位选第二组的哪个
for(int p = 0; p < m; p++){
// 将第一组中的i和第二组中的p连接起来,代价为cost.get(i).get(p)
ans = Math.min(ans, cost.get(i).get(p) + dfs(i-1, mask | (1 << p)));
}
return cache[i][mask] = ans;
}
}
优化:这里有重复寻找第二组中每个点成本最小的连接方式,可以进行预处理
class Solution {
int n, m;
int[][] cache;
int[] mincost;
List<List<Integer>> cost;
public int connectTwoGroups(List<List<Integer>> cost) {
this.cost = cost;
n = cost.size(); m = cost.get(0).size();
// 预处理寻找第二组中每个点的最小连接成本
mincost = new int[m];
Arrays.fill(mincost, Integer.MAX_VALUE);
for(int i = 0; i < m; i++){
for(List<Integer> c : cost){
mincost[i] = Math.min(mincost[i], c.get(i));
}
}
cache = new int[n][1 << m];
for(int i = 0; i < n; i++)
Arrays.fill(cache[i], -1);
return dfs(n-1, 0);
}
// 定义dfs(i, mask) 表示 在第一组中还有0-i个点需要连接,连接的第二组点在集合mask中,所需要的最小成本
// 转移:枚举第一组第i个点连接第二组中的任意一个点
// 递归边界: dfs(0, mask) ,此时mask中还为0的点可以连接任意第一组的点,选最小的成本
// 递归入口: dfs(全集,0)
public int dfs(int i, int mask){
if(i < 0){
if(mask == (1 << m) - 1)
return 0; // 第二组的点都选过了,没有额外成本
int ans = 0; // 寻找第二组中不为1的点,可以连接第一组任意点,选成本最小的点
for(int j = 0; j < m; j++){
if(((mask >> j) & 1) == 1) continue;
ans += mincost[j];
}
return ans;
}
if(cache[i][mask] >= 0) return cache[i][mask];
int ans = Integer.MAX_VALUE;
// 枚举第i位选第二组的哪个
for(int p = 0; p < m; p++){
// 将第一组中的i和第二组中的p连接起来,代价为cost.get(i).get(p)
ans = Math.min(ans, cost.get(i).get(p) + dfs(i-1, mask | (1 << p)));
}
return cache[i][mask] = ans;
}
}
问: 能不能枚举第二组的点,去连接第一组的点?
答: 也可以,但这样做的时间复杂度是 O(nm2^n),相比 O(nm2^m)更慢。注意本题 n >= m。
记忆化搜索转递推
class Solution {
// 在记忆化搜索中,存在一个状态 i < 0, 因此f数组整体右移
// 令f[0][x]表示状态 i < 0,最后返回结果f[n][(1 << m) - 1]
public int connectTwoGroups(List<List<Integer>> cost) {
int n = cost.size(), m = cost.get(0).size();
// 预处理寻找第二组中每个点的最小连接成本
int[] mincost = new int[m];
Arrays.fill(mincost, Integer.MAX_VALUE);
for(int i = 0; i < m; i++){
for(List<Integer> c : cost){
mincost[i] = Math.min(mincost[i], c.get(i));
}
}
int[][] f = new int[n+1][1 << m];
for(int i = 0; i < (1 << m); i++)
for(int j = 0; j < m; j++)
if((i >> j & 1) == 1) // 第二组的点 k 未连接
f[0][i] += mincost[j]; // 去第一组找个成本最小的点连接
for(int i = 0; i < n; i++)
for(int j = 0; j < (1 << m); j++){
int res = Integer.MAX_VALUE;
for(int k = 0; k < m; k++) // 第一组的点 i 与第二组的点 k
res = Math.min(res, f[i][j & ~(1 << k)] + cost.get(i).get(k));
f[i+1][j] = res;
}
return f[n][(1 << m) - 1];
}
}