python详解(7)——进阶(1)：排序算法

目录

一、前言

二、什么是算法（简单）

1、算法

2、排序算法

三、冒泡排序（中等）

 四、快速排序（困难）

五：插入排序（中等）

 六、选择排序（适中）

 七、计数排序（困难）

 八：归并排序（超难）

九：基数排序（困难）

十：bogo排序（宇宙超级无敌爆炸简单）

十一、尾声

一、前言

从现在开始，你就正式走出了入门圈。但是从入门到精通中间还有很长一段路要走。

python的大部分低级知识你已经掌握，我们不讲知识，而是讲算法。

排序算法，是最基本的算法之一。我们先来学习他。方法很多，挨个学吧。

写作不易，支持一波~

注意：标题有难易标注，可以根据自己的能力来选择学习。

---

二、什么是算法（简单）

1、算法

先来看看算法的基本定义。

来源：360百科

这就是算法。你可以尝试看懂他，看着很专业，其实静下心来一个字一个字看很简单。

简单说，算法就是解决一道题的完整指令。无论你输入什么（前提是规范），都能在有限时间内获得要求的输出。

我们研究下算法的基本5个性质。

1：有穷性。 算法必须是有结尾的，如果是一个死循环则称不上算法。必须在有限个步骤后终止。

2：确切性。算法的每一步必须有确切的定义，哪一步就是哪一步。

3：输入项。算法要让用户进行输入。但是有0个输入的情况，这就是算法本身定了初始条件。比如说要获取1-100的随机数，就不用用户输入麻烦人了。

4：输出项。输出结果，没有结果的算法是没意义的。必须得有。

5：可行性。也叫有效性。算法是针对实际问题进行设计的，你要让他能得到自己满意的结果。

接下来，研究算法的评定。

评定一个算法主要可以5方面来考虑。

1：时间复杂度，说人话就是代码运行时间能不能尽量短。

2：空间复杂度，就是算法消耗的内存空间，简单说就是占CPU的资源程度。

一般来说，要完成的问题规模越大，时间复杂度、空间复杂度就越大。

3：正确性，算法一定要对， 这个不必多说。

4：可读性，算法一定要方便用户理解。

5：健壮性，就是针对用户不合理输入的容错和处理能力。也叫作容错性。

算法有很多，基本的方法有递推法，递归法，分治法，穷举法，贪心算法，迭代法，动态规划法，分支界限法，回溯法等等等等。

---

2、排序算法

这篇文章，我们要学习算法之一：排序算法。

排序算法，就是将一个列表按照要求顺序排列。输入输出要求：

说人话：列表从无序变成有序。

排序算法高达20余种，360百科上有25种。

虽然说python里面有sort方法，但是sort方法的底层还是运用了这些算法的。

排序方法分为稳定性和不稳定性。比如，一个列表里两个元素相等放在一起，如果排序自始至终没有改变他们两个的相对位置，该排序算法就具有稳定性。

本文章，我们将要学习8种排序算法：

冒泡排序、快速排序、插入排序、选择排序、计数排序、归并排序、基数排序、bogo排序。

话不多说，现在开始：

---

三、冒泡排序（中等）

冒泡排序，名字有一点奇怪。属于稳定的。他对空间要求低。

我们先来了解冒泡排序的基本思路。

他的基本思路就是将列表的该项与后一项比较。排序从一个列表的第一项开始，将该项与后面一项进行比较，如果该项大于等于后面项则交换二者位置。这么一直遍历到最后一位。再返回第一位。

一直重复上述过程，直到1次遍历中，没有进行任何操作，就说明排序成功。

过程中，最大的数越来越往后“浮”出，故此叫做冒泡排序。

注意：如果你不懂range是什么，请先去学习range，不然理解起来很困难。

我们开始分析python实现。

首先，让用户输入列表里的每一项组合成列表:li。设置变量n为列表的长度。

接着，我们放一个for循环，用i遍历range(n-1)，就能保证能在循环结束后列表排列一定结束。

接着，我们再放一个for循环，用j遍历遍历range(列表长度-轮数)，还是range。

注意：这里面，列表的长度就是n，轮数就是i-1。减一是因为range(abc)是0到abc-1的数列，再减去1才是真实轮数。

每一次遍历都将本元素与下一个元素比较，交换。可以比较li[j]与li[j+1]的大小，大于则两数互换。

最后，输出列表。

完整代码：

def gulugulu_sort(li):#函数
    n=len(li)#n为列表的长度
    for i in range(n-1):#外层循环，遍历n-1次才能保证情况最坏也能正序排列
        print("轮数",i+1)#每次遍历输出轮数
        for j in range(n-i-1):#内层循环，遍历n-i-1次保证不多不少
            if li[j]>li[j+1]:#比较
                li[j],li[j+1]=li[j+1],li[j]#两数互换
                print("排序：",li)#输出
    return li
li = list(map(int,input().split()))#获取输入列表
print("最后结果:",gulugulu_sort(li))#输出

效果：

 瞎输入的一串：

结果： 

泰裤辣！！！！！！！！！

如果你需要把列表逆序排列，只用把代码里的大于改成小于就行了。

---

 四、快速排序（困难）

接下来，我们了解快速排序。这是对冒泡排序的改进。

来源：360百科

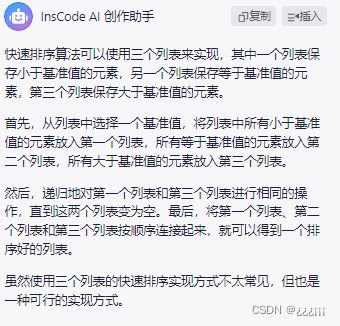
快速排序的基本思想就是将列表里的一个元素设置为key。注意：这个key值是什么都行，只要是列表里的元素，一般取第一和最后。之后将整个列表分成两个新列表：大于等于key的数，小于key的数。之后再将两个列表继续按照取key、分类的方法分，成4份，8份···一直分，直到每一个列表只有1或0个元素。就能排序成功。

快速排序也有很多方法实现。这里我们学习的是三列表法，感觉方便理解一点。

这是前后指针法，了解一下就行：

我们开始学习3列表法。先看创作助手的回答：

直接讲程序思路。首先，我们设置一个函数，让用户输入列表。我们把整个列表分成0和1个元素，多个元素两类。0,1个元素直接返回就行，多个元素再进行处理。

接着，我们将列表的第一个元素作为key。

我们创建三个新列表：left，right，middle。分别对应着三种情况：小于key，大于key，等于key。

之后用i去遍历原列表。如果i小于key，就添加到left列表里。如果等于key，就添加到middle列表里。如果大于key，则添加到right列表里。

上述代码如下：

def quick_sort(li):
    if len(li) <= 1:
        return li
    key = li[0]
    left,right,middle=[],[],[]
    for i in li:
        if i < key:
            left.append(i)
        elif i > key:
            right.append(i)
        else:
            middle.append(i)

有人要问了：但是我们要分隔left、right列表，分了还得再分，该怎么办呢？

接下来，我们给代码加上点睛之笔。在函数末尾添加：

    return quick_sort(left) + middle + quick_sort(right)

是不是豁然开朗？

一个函数可以调用自身，减少代码量。这种方法叫做递归。在算法里经常用到。该函数则叫做递归函数。

将left，right两个列表再次进行快速排序，因为形参虽然是left或right，实参仍然是li，定义域不同，所以他与第二个定义的left、right不会造成混淆。

之后再衍生出第二个left，right再次执行函数，再次排序，再次执行函数，再次排序······

当left、right都只剩一个数字的时候，就会通过上面的if条件返回。

递归函数中，总会有一个if条件来阻止陷入死循环，这个条件就叫做递归边界条件。

这时候，代码再一层层往上返回，一直到第一层，就可以输出已经正序排列的列表。

实数点睛之笔，加上这行代码，仿佛档次一下就上来了。

我相信，大家的理解能力一定比我强(doge

加上输出后，完整代码：

def quick_sort(li):#快速排列函数
    if len(li) <= 1:#如果长度是1或0
        return li#直接输出
    key = li[0]#key是第一位
    left,right,middle=[],[],[]#创建3列表
    for i in li:#遍历
        if i < key:#如果小于
            left.append(i)#添加到left
        elif i > key:#如果大于
            right.append(i)#添加到right
        else:#如果等于
            middle.append(i)#添加到middle
    global a#全局变量：轮数
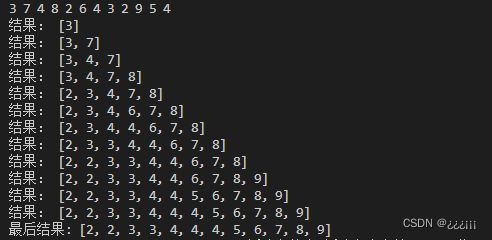
    a+=1#自增
    print("第",a,"趟，",end="")#输出轮数
    print(f"原列表为{li}，左为{left}，中为{middle}，右为{right}")#输出拆分结果
    return quick_sort(left) + middle + quick_sort(right)#返回，具体见文章解析
a=0
lst = list(map(int,input().split()))#获取列表
print(quick_sort(lst))#输出

最终结果：

 very good！

---

五：插入排序（中等）

先看基本简介。

（来源：360百科）

方法是：获取用户的输入列表1，创建一个空的列表2。

我们用i遍历列表1，如果列表2为空则直接将元素添加。如果列表2不为空则用j遍历列表2。

将列表1的每一个元素插入到列表2的合适地方，全部插入完就是正序排列了。

插入到合适位置，只用将该元素与列表2的每一个元素比大小，如果检测到该元素小于列表2的一个元素，就插入在他的前一位。如果最后一位还没有就直接添加到最后一位。

思路炒鸡煎蛋好吗？但是代码写起来有点难度。主要列表、range的位置很难分清，啥时候减一啥时候加一。

最终代码：

def insert_sort(li):#创建函数
    li1=[]#创建li1
    for i in range(len(li)):#大循环，遍历len(li)
        if not li1:#如果li1长度为0
            li1.append(li[i])#直接添加
        else:#如果li1有长度
            for j in range(len(li1)):#用j遍历li1的长度
                if li[i] < li1[j]:#比较大小，如果小于则应该插入到该位置
                    li1.insert(j,li[i])#插入
                    break#退出循环
                if j == len(li1)-1:#如果遍历到最后
                    li1.append(li[i])##直接在最后一位添加
                    break#退出循环
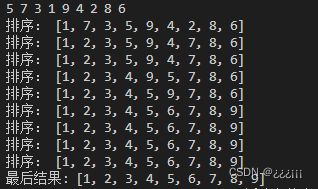
        print("结果：",li1)#输出一次插入后的结果
    return li1#返回
li = list(map(int,input().split()))#获取输入列表
print("最后结果:",insert_sort(li))#输出

结果：

真不戳！

---

 六、选择排序（适中）

选择排序，十分的简单，但是是一个不稳定的排序方法。

先看基本思想：

意思就是说，这种方法就是直接找最小的数。之后一个一个挨着找。看着思路，我相信你们自己也能完成。

思路：创建函数selection_sort ，获取参数li。

之后用i遍历range(len(li))。这里，i后面的部分叫做为排序部分。

再设置一个较小数变量：min_index=i。她用来记录较小值所在的位置。

再设置一个内层循环，查找最小值。用j遍历range(min_index+1,len(li))。+1是因为min_index这时候是未排序部分的第一个元素，没必要自己比自己。

如果li[j]比li[index]还小，j就是最小的。min_dex=j来更新数据。

内层循环结束后，将未排序的部分的第一个元素（i）与最小元素（min_index）交换位置。

整个函数结束，return li。

完整代码：

def selection_sort(li):
    for i in range(len(li)):#外层循环
        min_index=i#最小值所在位置为i
        for j in range(i+1, len(li)):#内层循环查找最小值
            if li[j] < li[min_index]:#如果找到比当前最小值还要小的元素
                min_index=j#更新最小值
        li[i],li[min_index]=li[min_index],li[i]#将未排序部分的第一个元素和最小值交换位置
        print("排序：",li)
    return li#返回排好序的列表
li = list(map(int,input().split()))#获取输入列表
print("最后结果:",selection_sort(li))#输出

输出：

 perfect！

---

 七、计数排序（困难）

大部分排序都是基于元素的比较。但是计数排序不一样。

首先，我们先创造一个空的列表。这里假设数字的范围为0-9，这样，我们就可以建一个0-9的数列。设用户输入的列表为li：

0 0 0 0 0 0 0 0 0 0

0 1 2 3 4 5 6 7 8 9                

假设列表为[1,2,3,4,6,4,3,5,7,4,8,9,3,0,7,0,2,6,3]

我们来统计0到9分别出现的次数：

2 1 1 4 3 1 2 2 1 1

0 1 2 3 4 5 6 7 8 9

这不就出来了吗？列表就是：

[0,0,1,2,3,3,3,3,4,4,4,5,6,6,7,7,8,9]

计数排序牺牲空间换取时间，相对于所有比较排序都是最快的。

但是，他有一个致命的缺点：前提范围内。给的数组最好是一定范围内的随机数，比如1到10。不然如果两个数据相差大，一个一个数得数到天荒地老。

接下来开始写程序。

因为计数排序一般程序的第二个循环太难李姐，所以我采用了3个列表。

列表1：输入的列表。

列表2：用来记录列表1里面所有数出现的数量

列表3：最终返回的列表。

这个代码思路比较难，我们讲一段写一段。

首先还是设置函数。

def count_sort(li):#计数排序函数

如果列表为空，要直接返回列表。如果不为空再开始下列程序。

    if not li:#如果列表为空
        return li#直接返回

首先，我们创建一个变量：k来保存列表li2应有的长度。他等于：列表的最大值-最小值+1.

之后再创造li2，为长度为k的全0列表。

    k=max(li)-min(li)+1#创建的列表应该有的长度
    li2=[0]*k#创建全0列表，长度为k

为啥要是最大值-最小值+1呢？比如：一个列表是[9,9,8,7,7,6,6,6,6]，那么li2的长度就应该是9-6+1=4。li2是长度为4的全0列表，就是[0,0,0,0]。

接下来，我们开始第一次遍历。对li1中每个元素出现的数量进行计数。

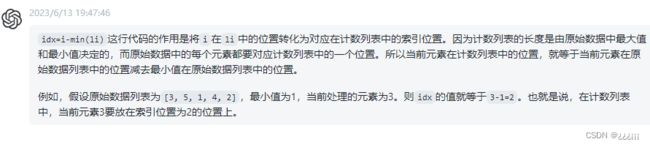
设置变量idx记录对应索引的位置，为i-min(li)。之后列表li2对应的位置自增。

    for i in li:#第一次遍历，进行计数
        idx=i-min(li)#查找索引位置
        li2[idx]+=1#对应位置自增
        print(li2)

为啥是i-min(li)呢？

因为这是该元素与最小值的差，li2是以min(li)为分界线的，所以要减去他。不理解？举个例子

还是列表[9,9,8,7,7,6,6,6,6]，这时li2=[0,0,0,0]。当i遍历到第0位时i=9，min(li)=6，9-6=3，所以就在列表的第三位自增，li2变成[0,0,0,1]。就成功在对应位置自增计数了。还是看不懂？

 来看ChatGPT的回答。懂了吧？

接着，我们创建列表li3.

    li3=[]#空列表li3

第二次遍历，用i去遍历列表2的长度，也就是k。

   for i in range(k):#第二次遍历，进行整理。遍历li2长度

重难点来临！！！

先看代码：

        li3+=[i+min(li)]*li2[i]#注释君已崩溃，请看解析

注：不知道列表加、乘运算的请先利用搜索引擎查看。

首先，[i+min(li)]这部分。由于之前我们减去了一个min(li)，再加回来才是真实的数值。

之后要让他乘上li2的i位，也就是这个元素出现的次数。

li3自增该列表，就相当于append的作用。

这段代码，其实是在li3的末尾添加上一个列表：[遍历的元素]*出现的次数 所得列表。

不懂，再来看ChatGPT的回答：

懂了吧？

最后，直接return li3就完成了计数排序。

完整代码：

def count_sort(li):#计数排序函数
    if not li:#如果列表为空
        return li#直接返回
    k=max(li)-min(li)+1#创建的列表应该有的长度
    li2=[0]*k#创建全0列表，长度为k
    for i in li:#第一次遍历，进行计数
        idx=i-min(li)#查找索引位置
        li2[idx]+=1#对应位置自增
        print(li2)
    li3=[]#空列表li3
    for i in range(k):#第二次遍历，进行整理。遍历li2长度
        li3+=[i+min(li)]*li2[i]#注释君已崩溃，请看解析
    return li3#返回
li = list(map(int,input().split()))#获取输入列表
print("最后结果:",count_sort(li))#输出

啊···想不出来什么词了。

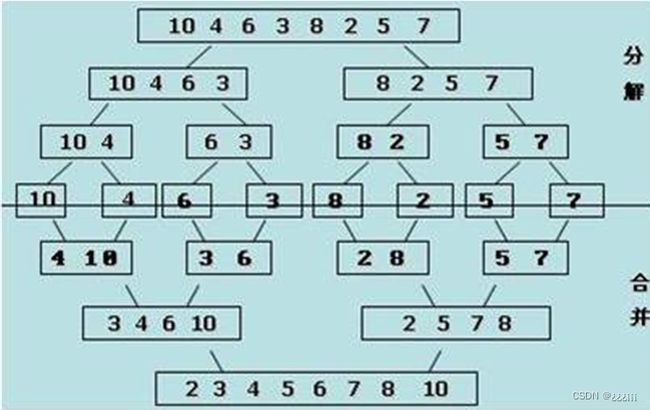
 八：归并排序（超难）

超难：归并排序闪亮登场！

 来源：360百科

接着放流程图：

看似十分简单、容易理解，但是写起来可是很有难度的。还是要进行递归的利用。

“归”很好理解，“并”有点难，我们边写代码边了解。（实际写起来归并都很难）

先说一个概念：将两个正序排列列表合并成一个正序排列列表，叫做二路归并。

归并排序就是利用的二路合并，先把列表变成长度为1的列表，因为长度为1的列表它本身就有序，就可以再利用二路归并的方法一步步得出结果。

注：此代码为ChatGPT所写，作者也无能为力······但是能理解就好了。

我们创建两个函数，一个处理归，一个处理并。

首先，创建函数merge_sort(li)。

因为需要用递归的方法，我们设置一个递归边界，还是len(li)<=1则直接返回。

def merge_sort(li):
    if len(li) <= 1:
        return li

之后设置一个变量mid，取列表的中间来把列表一分为二。

    mid = len(li) // 2

接着，我们设置2个变量：left_li和right_li，来保存0到mid和mid到最后一位。这就能把列表一分为二了。

    left_li = li[:mid]
    right_li = li[mid:]

OK，递归来了家人们：

    left_result = merge_sort(left_li)
    right_result = merge_sort(right_li)
    return merge(left_result, right_result)

不怕大家笑话，这段代码递归了个啥玩意儿，我看了3天没看明白。。。主要原因是没理解marge的作用。我以为是一直往上递归，最后用《2个列表保存多个分列表》

你只用记住merge函数是用来让2个列表二路归并的。具体怎么实现后面讲。

当这一行代码调用后，left_result就会再次二分二分二分，直到剩一个元素。

我们假设列表为[8,7,6,5,4,3,2,1]，变成[8][7][6][5][4][3][2][1]。我们用[8][7]做个例。

上一步，我们将[8,7]变成[8][7]，执行函数之后达到递归边界，最里层直接返回，left_result(倒数第二层的)就会接受到该列表：[8]。right_result就会接收[7]。

之后将[8][7]给merge进行二路归并处理，变成[7,8]。直接给上层的left_result。之后一直给一直给，就变成了正序排列的列表。

过程就是这样的：

(注：省略号处和前面的处理方法一样，懒得屑了)      
                             原：[8,7,6,5,4,3,2,1]

第一层：           left：[8,7,6,5]                        right:[4,3,2,1]

第二层：     left：[8,7]    right:[6,5]            left:[4,3]         right:[2,1]

第三层：left:[8] right:[7] left:[6] right:[5] left:[4] right:[3] left:[2]  right:[1]

第四层：到达递归边界，直接原列表返回————————————————————————————————————————————————

第三层：[8][7]二路归并为[7,8] [6][5]二路归并为[5,6]  ······             ······

第二层：[7,8][5,6]二路归并为[5,6,7,8]                         ······

第一层：[5,6,7,8][1,2,3,4]二路归并为[1,2,3,4,5,6,7,8]，直接返回

懂了吧？接下来我们研究怎么二路归并，要求：给两个有序列表，合成一个新有序列表。

开头还是先函数要参数，设置空列表，命名为result。

def merge(left, right):
    result = []

之后我们直接一口气看完：

    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    result += left
    result += right
    return result

还算好理解。第一行是为了判断两个列表是不是都不为空，不为空则进入循环。

第二行，如果比较两个列表的第0位。为什么是第0位后面说。

如果left<=right，那么result就添加left.pop(0)。

pop的作用方法是填上一个列表的索引位置，返回这个数，并且把这个数在列表里删除。

当条件成立，就说明left[0]是两个列表中最小的数，就让result添加上这个数，并且在left列表中删除他。这样下次循环就不会出现排序过元素数。

right同理。

循环结束后，可能一个列表是空，一个列表还有残余的元素。比如[1,2,3,4][2,5,7]，循环结束后左为空列表，右边的列表还有[5,7]存在。所以要自增两个列表才能将残余的元素也加进来。

最后直接返回就行了。

完整代码：

def merge_sort(li):
    if len(li) <= 1:
        return li
    mid = len(li) // 2
    left_li = li[:mid]
    right_li = li[mid:]
    left_result = merge_sort(left_li)
    right_result = merge_sort(right_li)
    print(left_result,right_result)
    return merge(left_result, right_result)
                
def merge(left, right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    result += left
    result += right
    return result
li = list(map(int,input().split()))
print(merge_sort(li))

九：基数排序（困难）

基数排序，名字听着有点像计数排序。他们都不是通过为个位比较来排序的。直接上一个范例：

一串数组，为46 49 24 58 21 56 24 19 44 22

我们放10个桶，分别对应着个位为0,1,2,3,4,5,6,7,8,9。

就可以分类为：

46 49 24 58 21 56 24 19 44 22
0：无
1:21
2:22
3：无
4：24 24 44
5：无
6:46 56
7：无
8:58
9:49 19

我们接着比十位。如果十位相同就看个位是咋排的。

46 49 24 58 21 56 24 19 44 22
0：无
1:19
2:21 22 24 24（排个位时，22在24前，21在22前）
3：无
4:44 46 49
5:56 58
6：无
7：无
8：无
9：无

如图所示。当我们比较百位时，发现没一个数字有百位，就可以直接排序：

结果就是：19 21 22 24 24 44 46 49 56 58。

网上找的图：

基数排序之所以我标的困难，是因为列表套列表的方式难。不知道二级列表的可以先查询相关资料。

接下来讲实现。首先还是创建函数。我们设置一个保存最大数的变量：max_num。再设置一个变量基数，每次循环后自乘10，来确定要侦测的位数。

def radix_sort(li):#创建函数
    max_num=max(li)#设置最大数
    base=1#基数

之后设置大循环。这次要用while。如果base<=max_num，就说明有数字超过base，进行下列程序。

    while base <= max_num:#如果大于，则循环结束

接着，我们创建10个篮，之后这10个篮要用一个大列表括起来。采取列表套列表的方式。就是：

[[],[],[],[],[],[],[],[],[],[]]

创建方法有点匪夷所思，但是只要知道能创建就行了。

        buckets=[[]for i in range(10)]#创建桶

之后我们用一个for循环遍历列表li，用来把每一个元素放在对应的桶中。

首先创建一个digit变量，保存的为(i//base)%10。啥意思呢？i//base就是这个元素整除base，再除以10得到余数。

        for i in li:#循环，用来把元素放入桶中
            digit=(i//base)%10#看要放在哪一个桶

难理解？举几个例子。

比如元素是66，要侦测他的十位数时，base是10，那就用66//10得到6，再除以10，得到余数6。

元素是114514，要侦测他的十位数时，base是10，那就用114514//10得到11451，再除以10，得到余数1.

嗯，就是这样。

之后，我们知道了放在哪个桶，就是加入到对应的篮中。

            buckets[digit].append(i)#放入桶

因为buckets里面是代表着0到9的10个列表，所以buckets[digit]才是要添加的篮。直接末尾添加。

之后，我们清空列表来不造成混淆。

        li.clear()#清空原列表

我们已经将所有元素储存到了列表buckets中。接下来，就是把这些元素按顺序再返回到原列表。

还是for循环遍历buckets，来遍历9个篮。

        for i in buckets:#循环，归位原列表

之后，我们在li的末尾直接添加该列表。

            li.extend(i)#末尾添加

extend：在原列表的末尾添加该可迭代对象。用li+=i也同理。

接下来，操作就基本结束。我们在加一句base=base*10，来遍历下一位。

完整代码：

def radix_sort(li):#创建函数
    max_num=max(li)#设置最大数
    base=1#基数
    while base <= max_num:#如果大于，则循环结束
        buckets=[[]for i in range(10)]#创建桶
        for i in li:#循环，用来把元素放入桶中
            digit=(i//base)%10#看要放在哪一个桶
            buckets[digit].append(i)#放入桶
        li.clear()#清空原列表
        for i in buckets:#循环，归位原列表
            li.extend(i)#末尾添加
        base=base*10#进行下一位
        print(li)
    return li#返回
li = list(map(int,input().split()))#获取输入列表
print("最后结果:",radix_sort(li))#输出

十：bogo排序（宇宙超级无敌爆炸简单）

bogo排序，又叫猴子排序。他是咋排的呢？

没有技巧！直接随机打乱！离谱不？

这种方法是最低效的方法之一。

这让我想起了一句话：给一只monkey一个计算机，总有一天他能敲出来一本《圣经》。

不说敲出来圣经，bogo排序，如果列表长到几万，几亿个元素，就快赶上猴子敲出来一段py代码的用时了。

这···我相信你们也能写出代码。

注：随机打乱列表可以用random的shuffle函数。用法：random.shuffle(列表)

直接上代码了。

import random
a=0
def bogo_sort(li):
    global a
    while True:
        a=1
        random.shuffle(li)
        for i in range(0,len(li)-1):
            if li[i]>li[i+1]:
                a=0
                break
        if a!=0:
            return li
li = list(map(int,input().split()))
print("最后结果:",bogo_sort(li))

就离谱~

十一、尾声

我们就学这八种排序算法，其他的太难辣。

脑细胞已经被杀光了(⊙︿⊙)如果这篇文章对你有帮助，请给个三连支持一下~

--------------------------------------------------------end---------------------------------------------------------------