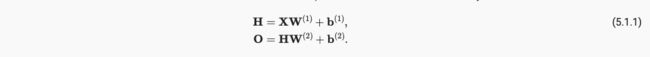d2l_第五章学习_Multilayer Perceptrons多层感知机
x.1 Hidden Layers
线性模型的基本假设是单调,即任何特征的增大都会导致模型的输出增大(权重正时,负值时亦)。但是现实中很多的关系并不仅仅是简单的线性关系,这个时候就需要引入非线性关系,而非线性关系由以下两个部分组成:Hidden Layer隐藏层和Activication Function激活函数。
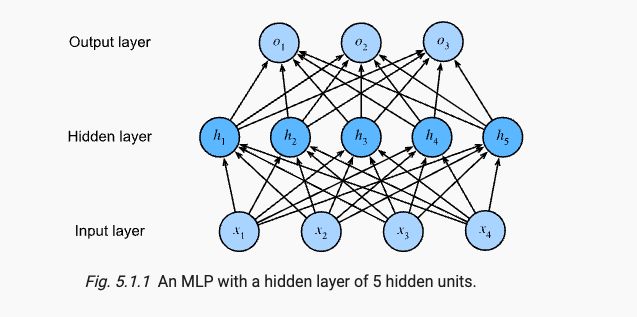
联想Regression/LInear Regression和Classification/Softmax Regression,二者的简洁实现都是由一个LazyLinear线性层实现,而这时我们再增加一层线性层,就通过引入隐藏层,构成了Multilayer Perceptrons多层感知机(后简写MLP)。如下图是具有两层(输入层不单独算一层)的MLP。它的第一层具有 4 ∗ ( 5 + 1 ) = 24 4*(5+1)=24 4∗(5+1)=24个可学习的参数,第二层具有 5 ∗ ( 3 + 1 ) = 20 5*(3+1)=20 5∗(3+1)=20个可学习参数。
x.2 Activation Function
x.2.1 From Linear to Nonlinear
通过引入hidden layer,我们的仿射函数具有如下变化,由(5.1.1)->(5.1.2)
仿射函数的仿射函数还是仿射函数,所以并没有引入非线性性质。为了引入非线性性质还得加入激活函数,通过激活函数,一层叠加一层,生成更有表达能力的模型,并且我们注意到,通用近似定理讲述了:通过使用更深(而不是更广)的网络,可以更容易逼近许多函数。
x.2.2 常见Activation Function
x.2.2.1 ReLU
ReLU是最常用的激活函数并且具有很多变种形式,如He_normal也是针对LeakyReLU和ReLU进行的权重初始化工作。
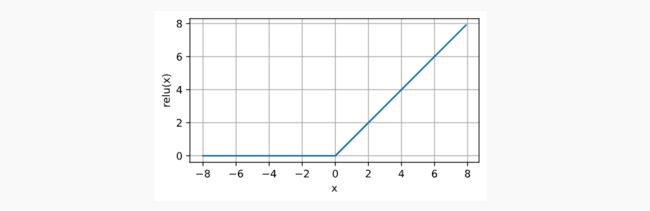
ReLU具有良好的求导的性质:要么让参数消失,要么让参数通过。它的函数表达式如下:
图像如下:
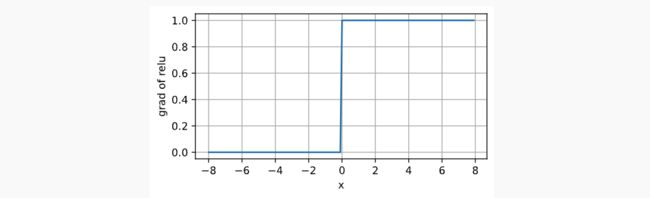
导数图像如下:
x.2.2.2 Sigmoid
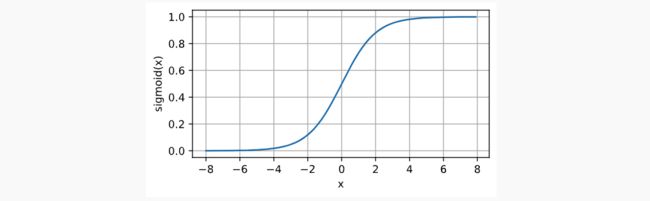
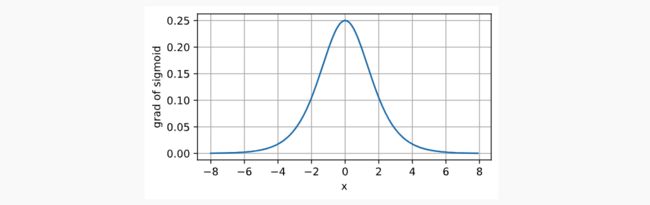
Sigmoid Function又称为Logistic Function,是在最早的神经网络中提出的,类似于一个阈值单元,档期输入低于某一个值时取0,高于某一阈值时取1。将范围从(-inf, inf)映射到(0, 1),函数表达,图像表达,导数图像表达如下:
x.2.2.3 Tanh
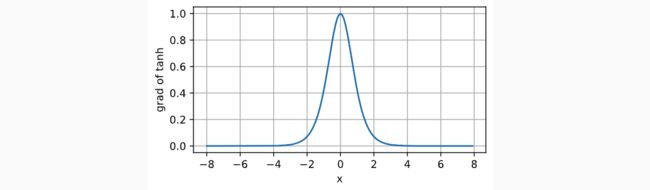
Tanh与sigmoid类似,只不过是将函数值映射从(0, 1)变成了(-1, 1)。它的函数表达式,函数图像和函数梯度图像如下所示:
x.3 MLP 复杂实现
复杂实现中可能要参考nn.Parameters函数接口,见https://blog.csdn.net/qq_43369406/article/details/131234557。
x.4 MLP 简易实现
MLP的简单实现即使用Pytorch封装好的nn.LazyLinear线性层代替nn.Parameter自己定义的权重层。在这一过程中,你可能需要接触到nn.Sequentail这个API,参考https://blog.csdn.net/qq_43369406/article/details/129998217
x.5 Forwad Propagation 正向传播, Backward Propagation 反向传播和 Computational Graphs 计算图.
通过使用nn的子类定义模型model,model便是生成的计算图。使用正向传播计算输出。使用反向传播更新model的梯度矩阵。使用optimizer.step()更新model的权重矩阵。
参考 一文搞懂网络训练中一个epoch中到底做了什么+zero_grad可以放在backward后面吗(train.py)https://blog.csdn.net/qq_43369406/article/details/129740629
x.6 Vanishing and Exploding Gradients 梯度消失和梯度爆炸
由于链式法则的运用,梯度其实是多个数值相乘的结果,当连续乘以一个大于1或者小于1的数,其结果都是非常不稳定的。
由此引申出Vanishing Gradients梯度消失和Exploding Gradients梯度爆炸的问题。
x.6.1 Vanishing Gradients 梯度消失
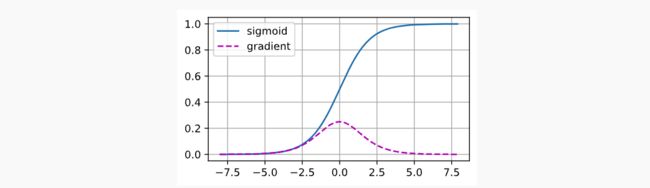
常见的梯度消失,如当一个极其小或者大的数字经过sigmoid函数后,它的求导数就会很小,无线趋近于0,这便是梯度消失,如下:
x.6.2 Exploding Gradients 梯度爆炸
如一百个均值为0,方差为1的矩阵相乘,很容易出现大于1的元素。
x.7 模型初始化
常见的初始化有数据初始化和模型初始化,而数据初始化有归一化,标准化等;模型初始化则有he_normal等。我们需要知道的是数据决定了你的山长什么样,模型初始化决定了你从哪里开始走。如果你刚开始就从一个局部最优开始走那情况将非常糟糕。
x.8 dropout
解决过拟合的根本目的是增强模型的泛化能力,而一个好的模型应该具备简单的特点。这里的简单有两点构成:
- 简单性以较小纬度的形式展现。如L2正则化减少了参数量。
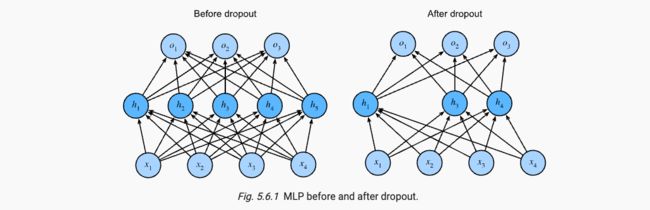
- 简单性的另一角度是增加平滑性,即函数不应对其输入的微小变化敏感。毕晓普证明具有输入噪声的训练等价于Tikhonov regularization,将该想法引入网络内部,得到了dropout层。dropout暂退法在前向传播过程中,在计算每一内部层的同时注入噪声,从表面上看像是在训练过程中丢弃一些神经元。
在Dropout层中,每个中间层的激活值h,以暂退概率p被一个新值(常为0)所替代,h’的期望仍为h。
相关代码参考https://github.com/yingmuzhi/deep_learning/blob/main/chapter5/5.6.%20Dropout.py