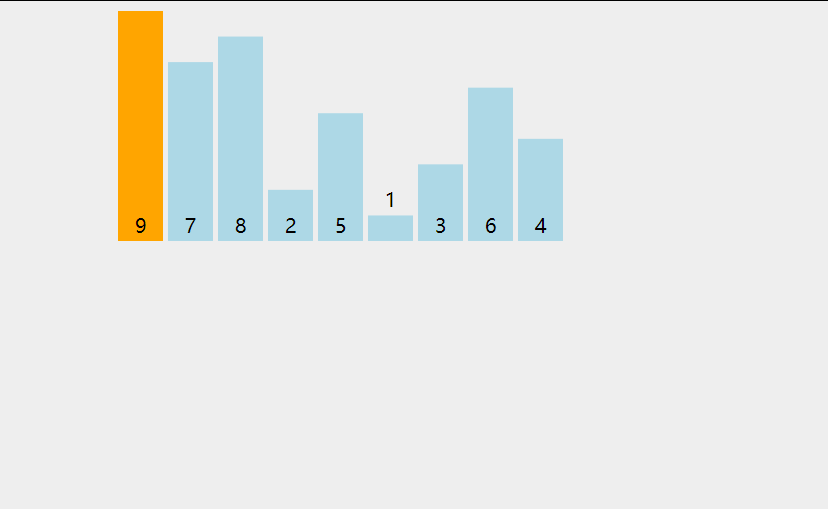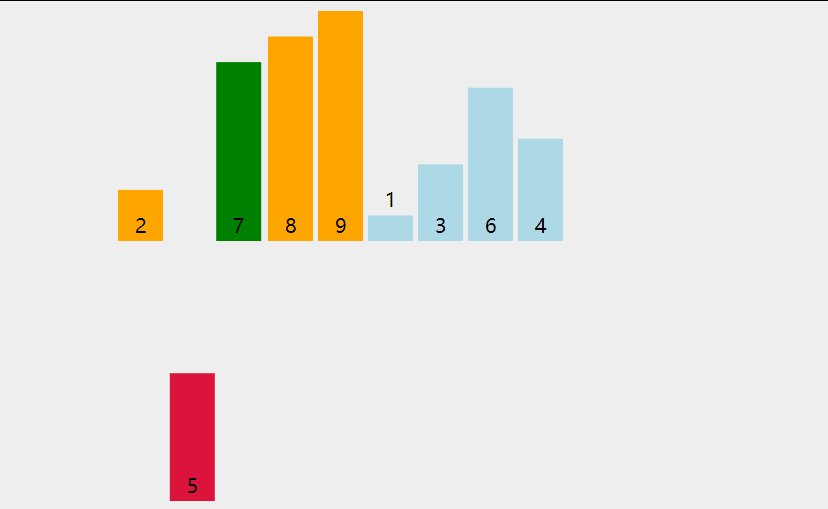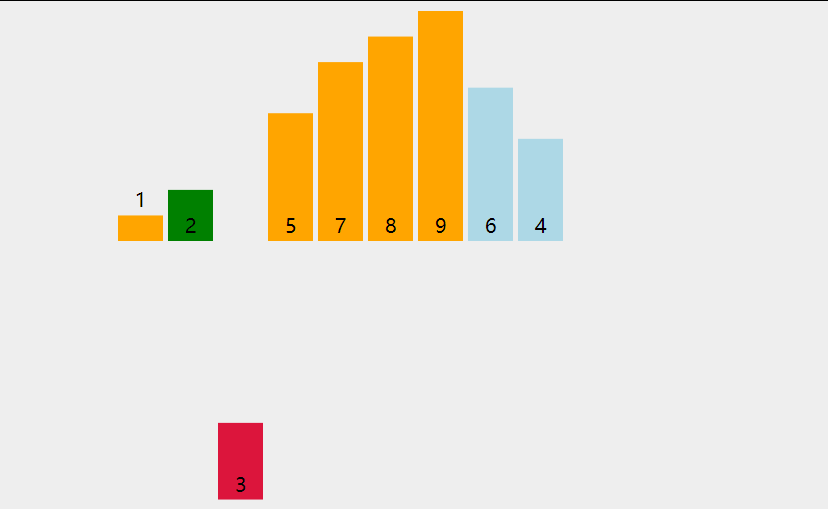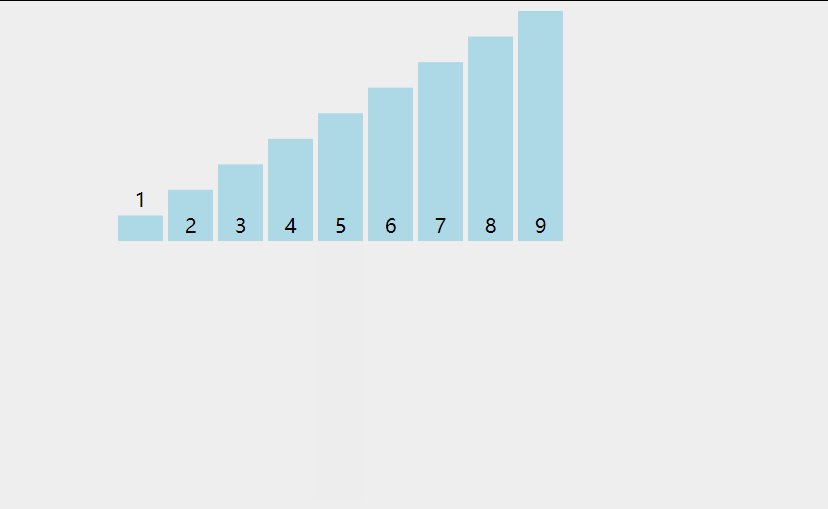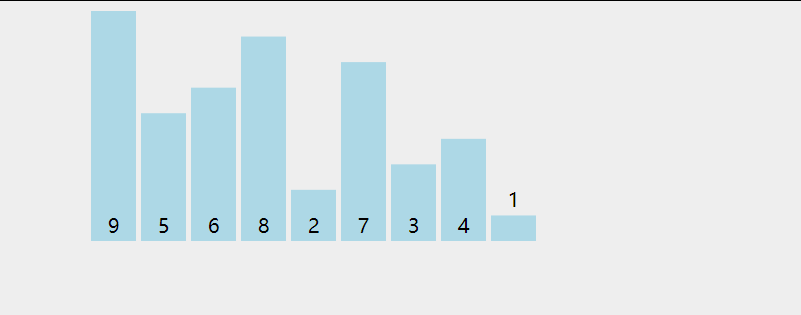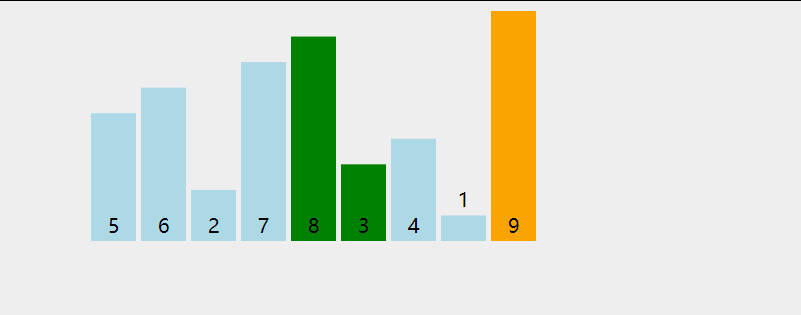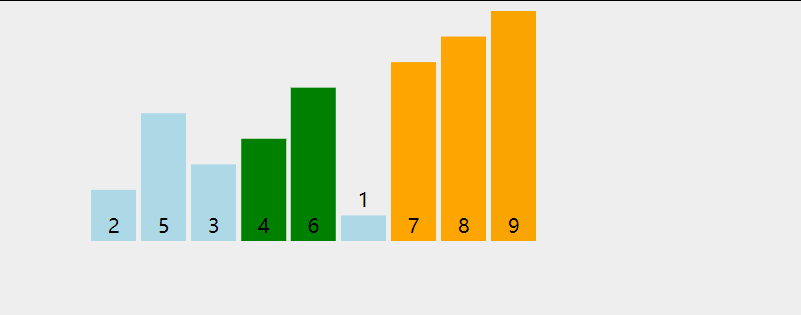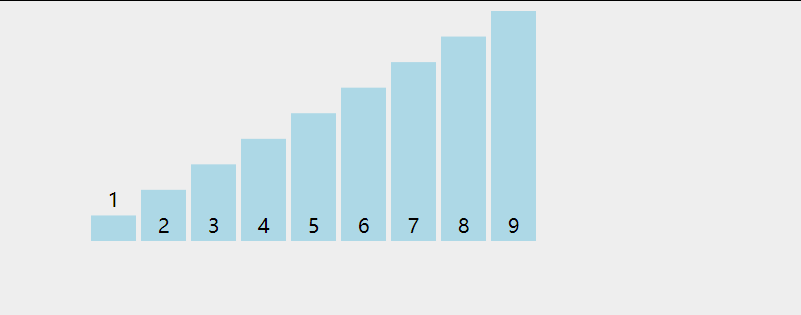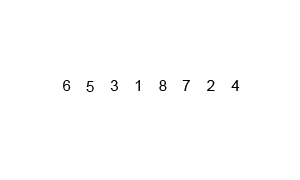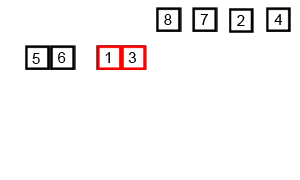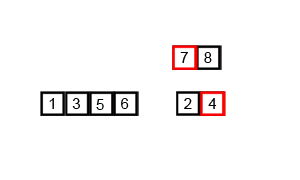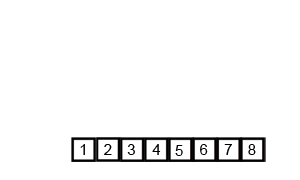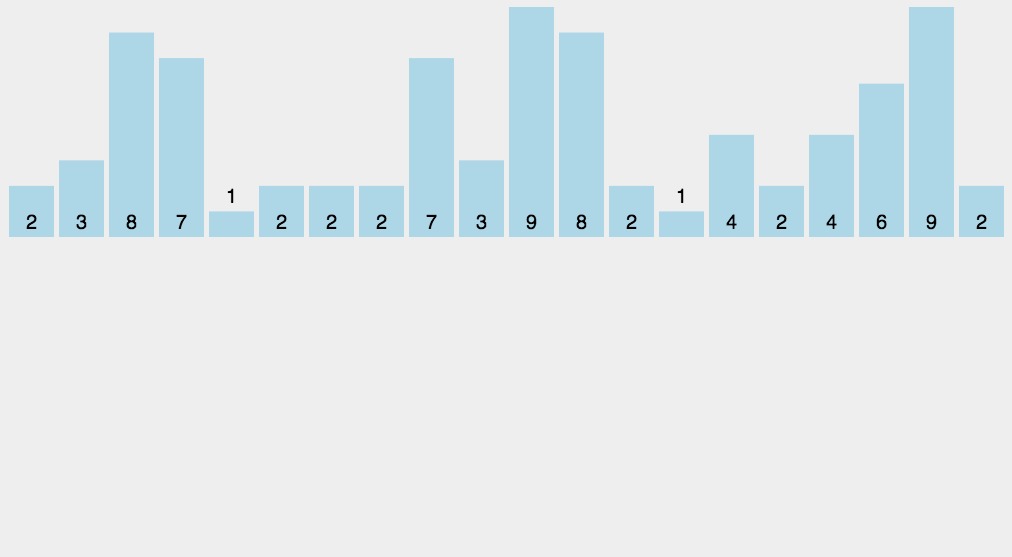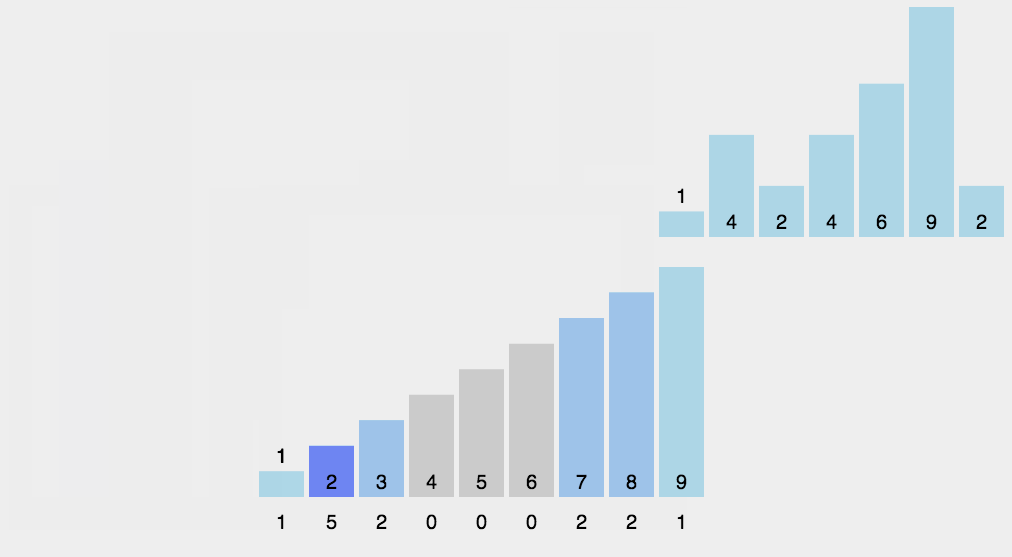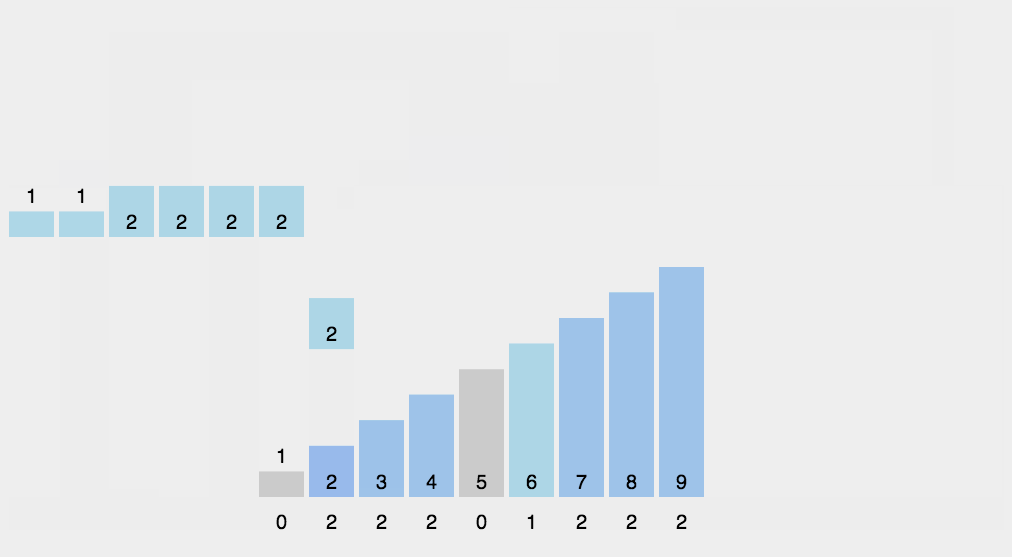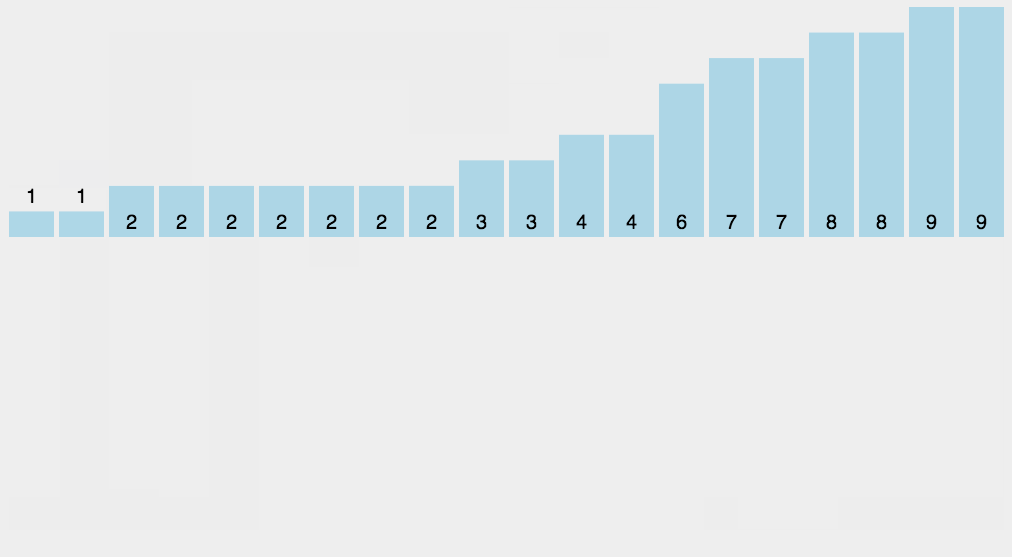十大基础算法
一、选择排序
过程简单描述:
首先,找到数组中最小的那个元素,其次,将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。其次,在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此往复,直到将整个数组排序。这种方法我们称之为选择排序。
为方便理解我还准备了动图:
.
public class SelectionSort {
public static void main(String[] args) {
int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
//定义内外两层循环,从最外层循环第一个值开始匹配,内层循环从外层循环加以开始向后匹配
//如果遇到小的值就进行交换
//外层循环到倒数第二为止,内层循环到倒数第一为止
for (int i = 0; i < arr.length-1; i++) {
int min = i;
for (int j = i+1; j < arr.length; j++) {
if(arr[i]>=arr[j]){
min = j;
int temp = arr[i];
arr[i] = arr[min];
arr[j] = temp;
}
}
}
CommonUtils.print(arr);
}
}性质:1、时间复杂度:O(n2) 2、空间复杂度:O(1) 3、非稳定排序 4、原地排序
二、插入排序
我们在玩打牌的时候,你是怎么整理那些牌的呢?一种简单的方法就是一张一张的来,将每一张牌插入到其他已经有序的牌中的适当位置。当我们给无序数组做排序的时候,为了要插入元素,我们需要腾出空间,将其余所有元素在插入之前都向右移动一位,这种算法我们称之为插入排序。
过程简单描述:
1、从数组第2个元素开始抽取元素。
2、把它与左边第一个元素比较,如果左边第一个元素比它大,则继续与左边第二个元素比较下去,直到遇到不比它大的元素,然后插到这个元素的右边。
3、继续选取第3,4,….n个元素,重复步骤 2 ,选择适当的位置插入。
为方便理解我还准备了动图:
public class InsertionSort {
public static void main(String[] args) {
int[] a = { 9, 3, 1, 4, 6, 8, 7, 5, 2 };
for (int i = 1; i < a.length; i++) {
//内层比较是从外层的赋值为起始点
//该值会和它前面的值比较,如果比前面的值小就交换
for (int j = i;j>0; j--) {
if(a[j]三、冒泡排序
1、把第一个元素与第二个元素比较,如果第一个比第二个大,则交换他们的位置。接着继续比较第二个与第三个元素,如果第二个比第三个大,则交换他们的位置….
我们对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样一趟比较交换下来之后,排在最右的元素就会是最大的数。
除去最右的元素,我们对剩余的元素做同样的工作,如此重复下去,直到排序完成。
为方便理解我还准备了动图:
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
for (int i = 0; i < arr.length; i++) {
//内层循环像指针一样指导着程序运行
for (int j = 0; j < arr.length-i-1; j++) {
if(arr[j]>arr[j+1]){
CommonUtils.swap(arr,j,j+1);
}
}
}
CommonUtils.print(arr);
}
}四、冒泡排序
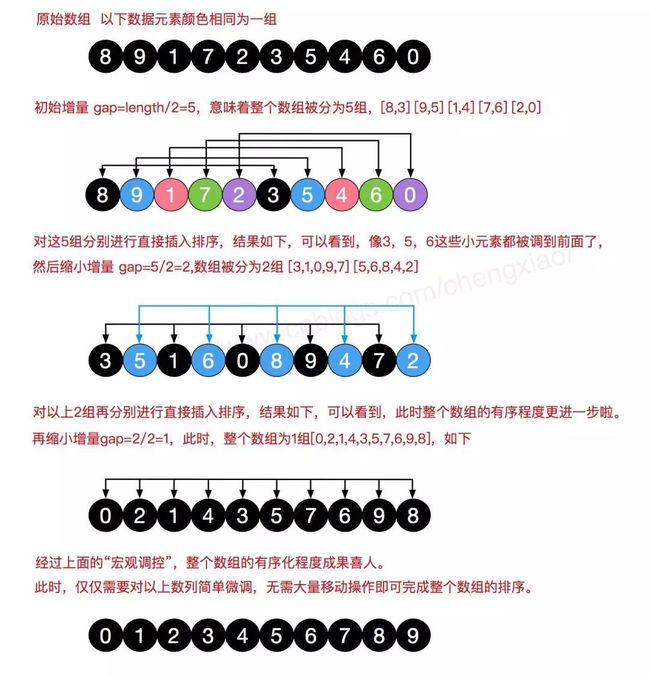
希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它正确的位置很远的话,则需要与相邻元素交换很多次才能到达正确的位置,这样是相对比较花时间了。
希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
希尔排序的思想是采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。
为方便理解我还准备了图片:
public class ShellSort {
public static void main(String[] args) {
int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
int h = arr.length/2;
for (int gap = h; gap > 0; gap--) {//间隔的循环
for (int j = 0; j < arr.length-gap; j++) {
if(arr[j]>arr[j+gap]){
CommonUtils.swap(arr,j,j+gap);
}
}
}
CommonUtils.print(arr);
}
}五、归并排序
将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很快的。
通过递归的方式将大的数组一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了,之后再把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的 ….. 直到全部小的数组合并起来。
为方便理解我还准备了动图:
public class MergeSort {
public static void main(String[] args) {
int[] arr = {1,4,7,8,3,6,9};
sort(arr, 0, arr.length-1);
CommonUtils.print(arr);
}
static void sort(int[] arr, int left, int right) {
if(left==right){
return;
}
int mid = left + (right-left)/2;
sort(arr,left,mid);
sort(arr,mid+1,right);
merge(arr,left,mid+1,right);
}
//先定义合并的方法
static void merge(int[] arr, int leftPtr, int rightPtr, int rightBound) {
int i = leftPtr;
int j = rightPtr;
int mid = rightPtr -1;
int[] temp = new int[rightBound - leftPtr + 1];
int tempPtr = 0;
//进行比较赋值
while (i<=mid&&j<=rightBound){
if(arr[i]>arr[j]){
temp[tempPtr]=arr[j];
j++;
tempPtr++;
}else {
temp[tempPtr]=arr[i];
i++;
tempPtr++;
}
}
//将未放入临时数组的数放入临时数组
while(i<=mid) temp[tempPtr++] = arr[i++];
while(j<=rightBound) temp[tempPtr++] = arr[j++];
//数组复制
for (int i1 = 0; i1 < temp.length; i1++) {
arr[leftPtr+i1]=temp[i1];
}
}
}六、快速排序
我们从数组中选择一个元素,我们把这个元素称之为中轴元素吧,然后把数组中所有小于中轴元素的元素放在其左边,所有大于或等于中轴元素的元素放在其右边,显然,此时中轴元素所处的位置的是有序的。也就是说,我们无需再移动中轴元素的位置。
从中轴元素那里开始把大的数组切割成两个小的数组(两个数组都不包含中轴元素),接着我们通过递归的方式,让中轴元素左边的数组和右边的数组也重复同样的操作,直到数组的大小为1,此时每个元素都处于有序的位置。
为方便理解我还准备了动图:
public class QuickSort {
public static void main(String[] args) {
int[] arr = {1,5,7,6,4};
sort(arr,0,arr.length-1);
CommonUtils.print(arr);
}
static void sort(int[] arr, int leftBound, int rightBound) {
if(leftBound>=rightBound) {
return;
}
int mid = partition(arr, leftBound, rightBound);
sort(arr,leftBound,mid-1);
sort(arr,mid+1,rightBound);
}
static int partition(int[] arr, int leftBound, int rightBound) {
int left = leftBound;
int mid = rightBound;
int right = rightBound-1;
while (left<=right){
//1、这两个指针分别寻找小于标杆和大于标杆的数,找到以后指针停止
//2、交换两边指针停止位置的数
//3、将标杆放到中间的位置
while (left<=right&&arr[left]<=arr[mid]){
left++;
}
while (left<=right&&arr[right]>arr[mid]){
right--;
}
if(left七、计数排序
计数排序是一种适合于最大值和最小值的差值不是不是很大的排序。
基本思想:就是把数组元素作为数组的下标,然后用一个临时数组统计该元素出现的次数,例如 temp[i] = m, 表示元素 i 一共出现了 m 次。最后再把临时数组统计的数据从小到大汇总起来,此时汇总起来是数据是有序的。
为方便理解我还准备了动图:
public class CountSort {
public static void main(String[] args) {
int[] arr = {2, 4, 2, 3, 7, 1, 1, 0, 0, 5, 6, 9, 8, 5, 7, 4, 0, 9};
int[] result = sort(arr);
CommonUtils.print(result);
}
public static int[] sort(int[] arr) {
int[] temp = new int[10];
for (int a : arr) {
temp[a]++;
}
int[] result = new int[arr.length];
int r = 0;
for (int i = 0; i < temp.length; i++) {
while (temp[i]>0){
result[r]=i;
r++;
temp[i]--;
}
}
return result;
}
}八、桶排序
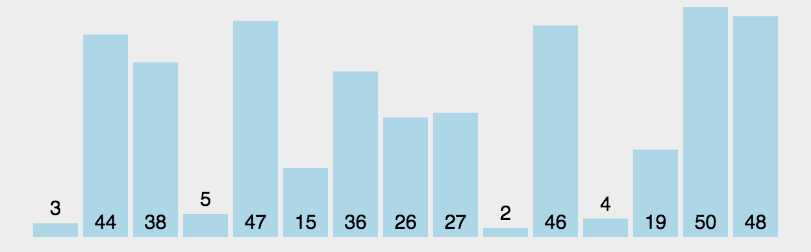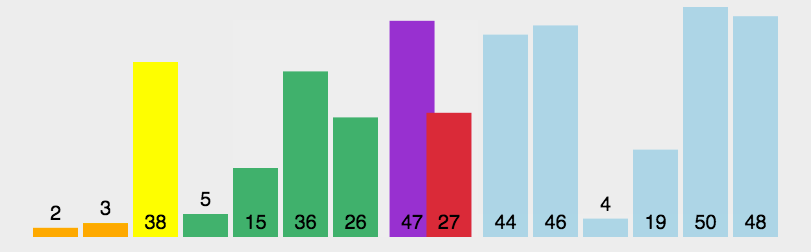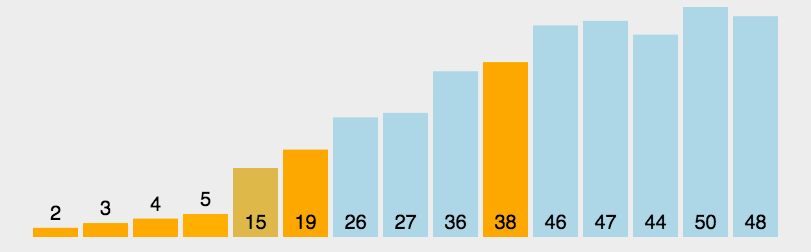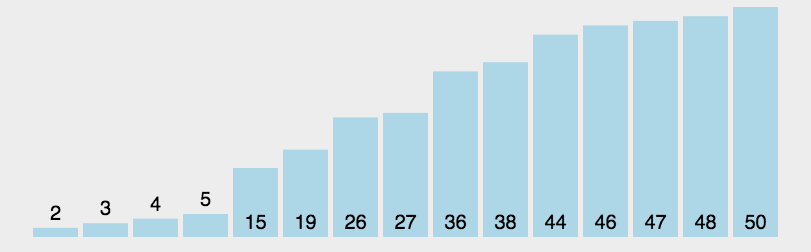
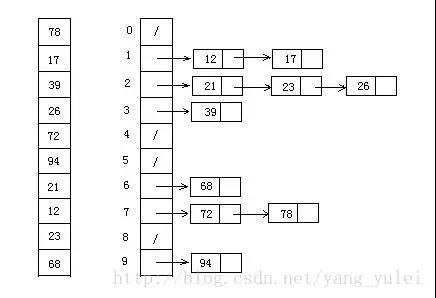
桶排序就是把最大值和最小值之间的数进行瓜分,例如分成 10 个区间,10个区间对应10个桶,我们把各元素放到对应区间的桶中去,再对每个桶中的数进行排序,可以采用归并排序,也可以采用快速排序之类的。
之后每个桶里面的数据就是有序的了,我们在进行合并汇总。
为方便理解我还准备了图片:
public class BucketSort {
public static void main(String[] args) {
int[] arr = {2, 4, 2, 3, 7,0};
int[] result = sort(arr);
CommonUtils.print(result);
}
public static int[] sort(int[] arr) {
int max = findMax(arr);
int mini = findMini(arr);
int group = (max-mini)/5+1;
List> totalBucket = new LinkedList<>();
//初始化桶
for (int i = 0; i < group; i++) {
totalBucket.add(new LinkedList());
}
for (int i = 0; i < arr.length; i++) {
//得到所在区间
int i1 = (arr[i] - mini) / (max - mini);
//向所在区间添加元素
totalBucket.get(i1).add(arr[i]);
}
//复制结果
for (List integers : totalBucket) {
Collections.sort(integers);
}
//复制结果
int[] result = new int[arr.length];
int r = 0;
for (int i = 0; i < totalBucket.size(); i++) {
for (int i1 = 0; i1 < totalBucket.get(i).size(); i1++) {
result[r]= totalBucket.get(i).get(i1);
r++;
}
}
return result;
}
public static int findMax(int[] arr) {
int max = arr[0];
for (int i : arr) {
if(i>max){
max = i;
}
}
return max;
}
public static int findMini(int[] arr) {
int mini = arr[0];
for (int i : arr) {
if(i 九、基数排序
基数排序的排序思路是这样的:先以个位数的大小来对数据进行排序,接着以十位数的大小来多数进行排序,接着以百位数的大小……
排到最后,就是一组有序的元素了。不过,他在以某位数进行排序的时候,是用“桶”来排序的。
由于某位数(个位/十位….,不是一整个数)的大小范围为0-9,所以我们需要10个桶,然后把具有相同数值的数放进同一个桶里,之后再把桶里的数按照0号桶到9号桶的顺序取出来,这样一趟下来,按照某位数的排序就完成了
为方便理解我还准备了动图:
public class RadioSort {
public static void main(String[] args) {
int[] arr = {5, 3, 6, 8, 100, 7, 9, 4, 20};
sort(arr);
CommonUtils.print(arr);
}
public static int[] sort(int[] arr) {
if(arr==null||arr.length==2) {
return arr;
}
int max = findMax(arr);
int num = 1;
while (max/10>0){
max= max/10;
num++;
}
List> totalBucket = new LinkedList<>();
//初始化桶
for (int i = 0; i < 10; i++) {
totalBucket.add(new LinkedList());
}
for (int i = 0; i < num; i++) {
//放入对应的桶
for (int j = 0; j < arr.length; j++) {
int location = (arr[j] / (int)Math.pow(10,i)) % 10;
totalBucket.get(location).add(arr[j]);
}
int k = 0;
for (List integers : totalBucket) {
for (Integer integer : integers) {
arr[k++]=integer;
}
integers.clear();
}
}
return arr;
}
public static int findMax(int[] arr) {
int max = arr[0];
for (int i : arr) {
if(i>max){
max = i;
}
}
return max;
}
} 十、堆排序
堆的特点就是堆顶的元素是一个最值,大顶堆的堆顶是最大值,小顶堆则是最小值。
堆排序就是把堆顶的元素与最后一个元素交换,交换之后破坏了堆的特性,我们再把堆中剩余的元素再次构成一个大顶堆,然后再把堆顶元素与最后第二个元素交换….如此往复下去,等到剩余的元素只有一个的时候,此时的数组就是有序的了。
为方便理解我还准备了动图:
public class HeadSort {
public static void main(String[] args) {
int[] arr = {5, 3, 6, 8, 100, 7, 9, 4, 20};
int n = arr.length;
//构建大顶堆
for (int i = (n - 2) / 2; i >= 0; i--) {
sort(arr, i, n - 1);
}
//进行堆排序
for (int i = n - 1; i >= 1; i--) {
// 把堆顶元素与最后一个元素交换
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
// 把打乱的堆进行调整,恢复堆的特性
sort(arr, 0, i - 1);
}
CommonUtils.print(arr);
}
public static void sort(int[] arr,int parent, int n) {
int child = 2*parent+1;
while (childarr[parent]){
CommonUtils.swap(arr,child,parent);
}
parent = child;
child = 2*parent+1;
}
}
}
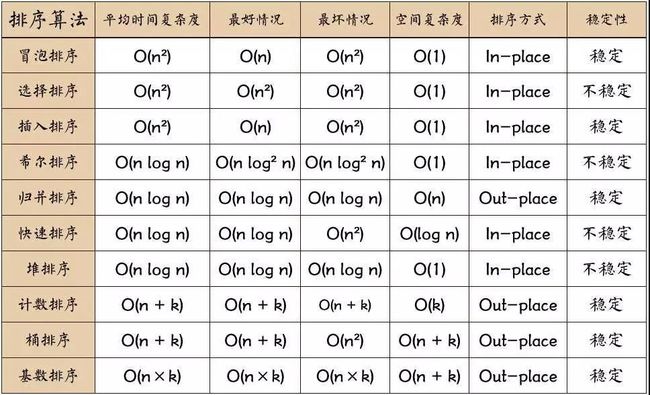
总结
用一张图汇总了10大排序算法的性质
参考文章:
堆排序详细图解(通俗易懂)_右大臣的博客-CSDN博客
https://www.cnblogs.com/itsharehome/p/11058010.html