机器学习中常用的模型评价指标及其应用场景
文章目录
- Accuracy, Recall, Precision, F-score
- 关于Precision, Recall的选择
- Micro-F1 & Macro-F1
- ROC、AUC
-
- ROC的绘制过程
- AUC
- 为什么要用ROC/AUC呢?
Accuracy, Recall, Precision, F-score
先看一下它们的计算公式:
A C C = T P + T N T P + F N + T N + F P R e c a l l = T P T P + F N P r e c i s i o n = T P T P + F P ACC = \frac{TP + TN}{TP+FN+TN+FP}\quad Recall = \frac{TP}{TP+FN}\quad Precision = \frac{TP}{TP+FP} ACC=TP+FN+TN+FPTP+TNRecall=TP+FNTPPrecision=TP+FPTP
在二分类任务中,通常将两个类别分为正类(+1)和负类(-1)。可以根据模型的预测结果和标签构建模型预测的混淆矩阵,混淆矩阵也是很多二分类指标建立的基础,混淆矩阵 (Confusion Matrix) 见图1:

关于混淆矩阵中的 T P , F P , F N , T N TP, FP, FN, TN TP,FP,FN,TN:
- T P TP TP:预测为正类,实际为正类的样本;
- F P FP FP:预测为正类,实际为负类的样本,即模型把负类样本预测成了正类;
- F N FN FN:预测为负类,实际为正类的样本,即模型把正类样本预测成了负类;
- T N TN TN:预测为负类,实际为负类的样本;
Accuracy、Recall、Precision都是构建在混淆矩阵的二分类指标:
- A c c u r a c y Accuracy Accuracy:模型预测正确的样本( T P + T N TP+TN TP+TN)占总样本( T P + F N + T N + F P TP+FN+TN+FP TP+FN+TN+FP)的比例;
- R e c a l l Recall Recall:模型预测的正样本( T P TP TP)占真实正样本( T P + F N TP+FN TP+FN)的比例,即真实的正样本被模型找出来的比例,因此也叫召回率;
- P r e c i s i o n Precision Precision:模型预测的正样本( T P + F P TP+FP TP+FP)里有多少是真的正样本( T P TP TP),即模型预测的正样本有多少是对的,因此也叫精确率;
F-score 是对 R(Recall), P(Precision) 的一个综合评价, β \beta β度量了 R 相对于 P 的重要性, 可以理解为 β = i m p o r t a n c e ( R ) i m p o r t a n c e ( P ) \beta = \frac{importance(R) }{importance(P)} β=importance(P)importance(R), 则表示 β \beta β越大, 我们越看重R.
F β = ( 1 + β 2 ) P ⋅ R β 2 P + R F_\beta = (1 + \beta^2)\frac{P \cdot R}{\beta^2 P + R} Fβ=(1+β2)β2P+RP⋅R
关于Precision, Recall的选择
这几个指标在很多任务中都有应用, , 但是不同的指标侧重于不同的方面, 比如P、R都有不同的侧重, 但看一个指标是比较片面的, 并不能反映出模型真实的效果. 有可能P很高, 但是R很低, 而在一些场景下R是很重要的.
比如在金融风控等领域, 我们希望算法能够尽量识别出所有有可能有风险的用户, 这时候就侧重于 Recall, 即希望算法把所有的正样本 (通常有危险的, 需要被找出来的被标记为正样本) 都筛选出来, 即使将所有样本都标为正 (即 Recall=1) . 因为这种情况下, 可能漏掉一个正样本带来的代价是极大的, 通常筛选完之后还需要交给人工进行判断. 类似的场景还有癌症检测, 将一个没有癌症的判断为癌症没有很大关系, 但是将一个有癌症的判断为没有癌症则是很严重的, 会出人命的!!!
又比如在垃圾邮件分类中, 我们可能更侧重于Precision. 我们希望算法在识别垃圾邮件时不要把正常邮件错分了, 这个时候希望Precision尽可能高, 即使将所有样本标为负也没关系 (TP=0时可认为Precision=1) , 或者说算法只把自己十分确信为垃圾邮件的标为正, 尽量降低FP, 即尽量不要把正常邮件视为垃圾邮件, 不然错过了offer那可咋整!!!
通常, 将需要识别出的类别, 或者简单的说坏的一类为正样本, 为什么呢?因为好的漏掉一般不会产生啥大的影响, 但是坏的跑了课就不行了!当然, 也需要不同场景下选择合适的指标!!!
我们是贪心的, 因此就有了一些综合的指标, 比如F-score. Precision是以被分类的所有样本为分母, Recall则是以原本所有的positives元素为分母. 二者之间并没有建立直接联系, 如果一个分类器, Precision很高但是Recall很低, 或者Recall很高但是Precision很低, 这两种分类器都是不好的, 都是我们不希望的. 所以我们采用F1-Score来建立Precision和Recall的联系.
在数学中, 调和平均数是永远小于等于算术均值平均数的, 当用于求两个数的平均数时, 如果直接用算术平均作为结果, 那么两数之间的差异将被大的值削平, 而调和平均数则不会极大削平这种大的差异, 得到的结果更倾向于小的值。
Micro-F1 & Macro-F1
基本的F1使针对二分类任务而言的, 在多分类中中, Micro-F1和Macro-F1是两种求多类别F1均值的方式.
- Micro-F1: 分别计算每个类别的 T P , F N , F P TP, FN, FP TP,FN,FP, 再求整体的 R e c a l l Recall Recall, P r e c i s i o n Precision Precision, 再以整体的 P , R P, R P,R来求 F 1 F1 F1, 得到Micro-F1. 在计算公式中考虑到了每个类别的数量, 所以适用于数据分布不平衡的情况; 但同时因为考虑到数据的数量, 所以在数据极度不平衡的情况下, 数量较多的类 (即常见的类) 会较大的影响到F1的值;
- Macro-F1: 分别计算每个类别的F1, 再求平均, 得到Macro-F1. 没有考虑到数据的数量, 所以会平等的看待每一类 (因为每一类的precision和recall都在0-1之间) , 会相对受高 P r e c i s i o n Precision Precision和高 R e c a l l Recall Recall类 (即稀有的类) 的影响较大;
M i c r o − F 1 Micro-F1 Micro−F1公式如下所示:
R e c a l l m i = ∑ i T P i ∑ i T P i + ∑ i F N i P r e c i s i o n m i = ∑ i T P i ∑ i T P i + ∑ i F P i M i c r o − F 1 = R e c a l l m i × P r e c i s i o n m i R e c a l l m i + P r e c i s i o n m i \begin{aligned} Recall_{m i} &=\frac{\sum_i TP_{i}}{\sum_i TP_{i} + \sum_i FN_{i}} \\ Precision_{m i} &=\frac{\sum_i TP_{i}}{\sum_i TP_{i} + \sum_i FP_{i}} \\ Micro-F1 &= \frac{ Recall_{m i} \times Precision_{m i}}{Recall_{m i}+ Precision_{m i}} \end{aligned} RecallmiPrecisionmiMicro−F1=∑iTPi+∑iFNi∑iTPi=∑iTPi+∑iFPi∑iTPi=Recallmi+PrecisionmiRecallmi×Precisionmi
M a c r o − F 1 Macro-F1 Macro−F1如下所示:
M a c r o − F 1 = 2 ∑ i F 1 i N Macro-F1 =2 \frac{ \sum_i F1_i}{N} Macro−F1=2N∑iF1i
ROC、AUC
接收者操作特征曲线 (recevier operating characteristic curve) , 用于反映一个而分类器的灵敏度 (sensitivity) 和特异度 (specificity) 之间的关系.
S e n s i t i v i t y = T P T P + F N S p e c i f i c i t y = T N T N + F P \begin{aligned} Sensitivity &= \frac{TP}{TP + FN}\\ Specificity &= \frac{TN}{TN + FP} \end{aligned} SensitivitySpecificity=TP+FNTP=TN+FPTN
其中Sensitivity也就是TPR (True Positive Rate) , 也就是Recall, Specificity是TNR (True Negtive Rate) . ROC的横坐标是 1 − S p e c i f i c i t y 1 - Specificity 1−Specificity, 即FPR (False Positive Rate, 即负样本中有多少被分成了正样本) , 纵坐标是Sensitivity. 横坐标表示的是负样本中被预测为正样本的比例, 纵坐标表示的是正样本中被预测为正样本的比例.
ROC如图2所示.
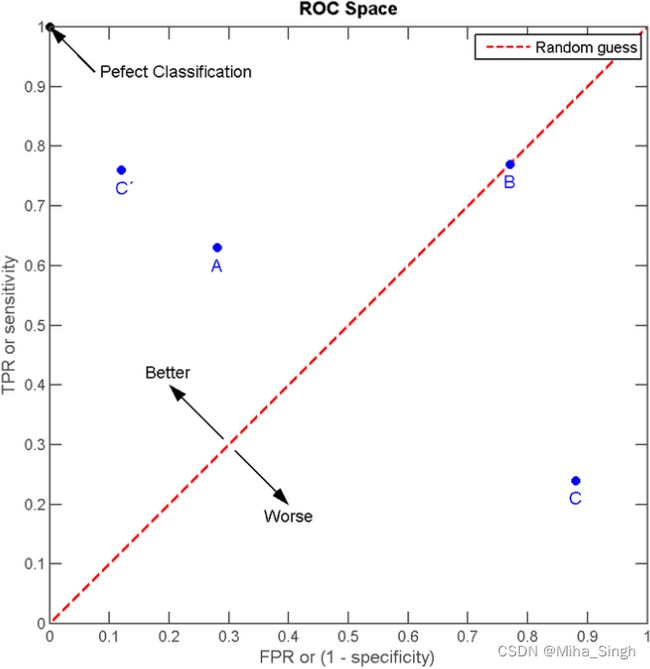
ROC的绘制过程
对于一个二分类问题, 使用一个分类器对样本集进行预测后, 可以得到每个样本属于正样本的概率, 此时我们还需要一个阈值来确定那些为正样本. 每选取一个阈值, 就可以得到一个 (TPR, FPR) 数值对. 当阈值从1到0不断减小时, 被确定为正样本的样本数不断增大, 其中TP和FP都会不断增大, 由于正负样本的数量是固定的 (即TPR, FPR的分母是固定的) , 则TPR和FPR都会不断增大. 那么,
- 当阈值为1时, (几乎) 所有样本都为负样本, 则TPR约为0, 既然都为负样本那么FP也为0, 则FPR也为0;
- 当阈值为0时, 所有样本都为正样本, 那么肯定所有的正样本都找出来了, 则TPR为1, 由于所有样本都预测为正样本, 那么肯定所有的负样本都预测为了正样本, 则FPR为1;
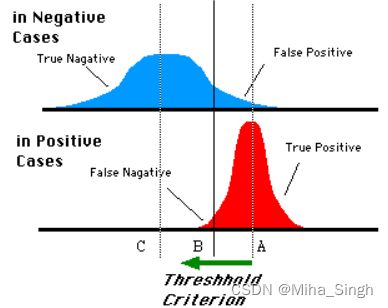
因此, 在阈值从1到0的过程中, (TPR, FPR) 不断增大, 从坐标 (0, 0) 到 (1, 1) , 如图3所示, 图3上部分为负样本为正样本的概率的分布图 (即横坐标为正样本概率值, 纵坐标为对应的样本数量) , 下部分为正样本为正样本的概率的分布图, 可见, 当阈值为 B B B时, 大部分正样本都被分为了正样本 (TP) , 小部分负样本被分为了正样本 (FP) . 由图4可见, 当阈值减小时, (TPR, FPR) 的变化过程.
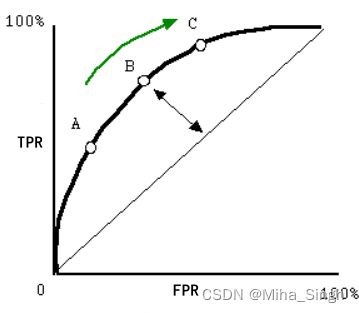
AUC
ROC是一个曲线, 那怎么作为一个指标呢? — 取ROC与坐标轴围成的面积, 即AUC (Area Under Curve). 由于ROC的绘制过程, 我们希望当阈值为接近0时, TPR尽量高, FPR尽量低 (其实不管阈值为何值, 都希望有这个效果) , 一个好的分类器的ROC的AUC应该尽量大.
AUC的含义: 随机挑选一个正样本、一个负样本, 分类器分别给出一个分数, 正样本的分数大于负样本的分数的概率. 强烈推荐-相关证明: 理解 ROC 和 AUC (以及 AUC 的简洁计算方式).
为什么要用ROC/AUC呢?
因为ROC曲线有个很好的特性: 当测试集中的正负样本的分布变化的时候, ROC曲线能够保持不变. 在实际的数据集中经常会出现类不平衡(class imbalance)现象, 即负样本比正样本多很多(或者相反), 而且测试数据中的正负样本的分布也可能随着时间变化. roc曲线不变原因: TPR和FPR是实际label内部的操作, 看混淆矩阵和tpr、fpr计算公式, 无论实际label比例怎么变化, tpr、fpr计算公式都是在实际为p或者n的内部计算的. AUC 关注的是样本间的排序效果. AUC 对正负样本比例的不敏感性: AUC: 直观理解AUC为何会对正负样本数分布不均匀情况鲁棒.
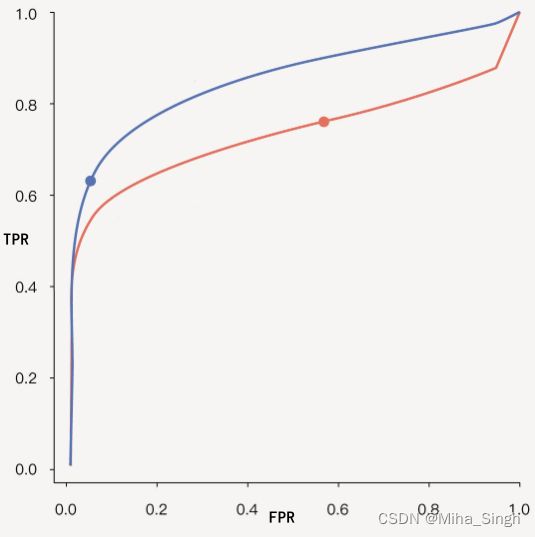
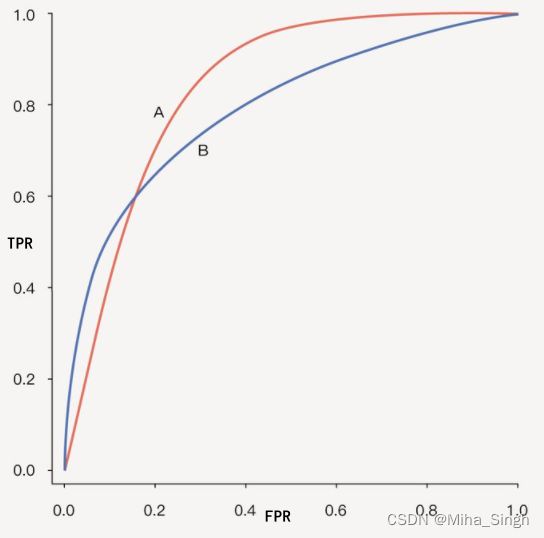
**如何使用ROC来选择模型?**当我们有多个分类器时, 给定一个数据集, 可以得到多条ROC曲线, 那么怎么来选择模型呢?一个很直观的想法是直接比较AUC. 但是在不同场景下, 我们要结合更看重的指标选择模型. 如图5所示, 当ROC不交叉时, 可以直接选择AUC高的;如图6所示,当ROC交叉时则需要慎重考虑了. 当需要高的Sensitiviy时, 选择A, 需要高Specificity (即低FPR) 时选择B.
参考资料:
- 分类模型评估之ROC-AUC曲线和PRC曲线;
- ROC曲线;