C语言建立并查集
一.树的存储方式
在知道并查集之前,我们得知道树的三种存储方式:
1.双亲表示法
双亲表示法 :双亲表示法是最简单的一种存储方式,它使用一个大小为n的一维数组来表示树中的n个节点。在数组中,每个元素存储该节点的父节点的下标,根节点的父节点下标为-1。由于每个节点只有一个父节点,因此可以快速找到一个节点的父节点,但查找一个节点的子节点需要遍历整个数组,效率较低。
用C语言定义其存储结构:
#define MAX_TREE_SIZE 100
typedef struct {
int data; // 节点数据
int parent; // 父节点在数组中的下标
} PTNode;
typedef struct {
PTNode nodes[MAX_TREE_SIZE]; // 存储节点的数组
int root; // 根节点在数组中的下标
int size; // 树中节点的个数
} PTree;
在上面的代码中,PTNode结构体表示树中的一个节点,包含节点的数据和其父节点在数组中的下标。PTree结构体表示整棵树,包括存储节点的数组、根节点在数组中的下标和树中节点的个数。可以根据需要调整MAX_TREE_SIZE的值来适应具体情况。
本次实验并查集就是用这种方法表示的
2.孩子表示法
孩子表示法采用链式存储结构,每个节点包含指向其第一个子节点的指针和指向其下一个兄弟节点的指针。如果一个节点没有子节点,则其子节点指针为空。孩子表示法的优点是查找一个节点的子节点很方便,但查找一个节点的父节点需要遍历整棵树。
这种方法我们最熟悉了,前面的二叉树和哈夫曼树的相关操作,我们都是用这种方法。
用C语言实现其存储结构:
#define MAX_TREE_SIZE 100
typedef struct CTNode {
int child; // 子节点在数组中的下标
struct CTNode* next; // 指向下一个兄弟节点的指针
} *ChildPtr;
3.孩子兄弟表示法(二叉树表示法)
孩子兄弟表示法也采用链式存储结构,每个节点包含指向其第一个子节点的指针和指向其下一个兄弟节点的指针。如果一个节点没有子节点,则其子节点指针为空;如果一个节点没有兄弟节点,则其兄弟节点指针为空。孩子兄弟表示法可以方便地遍历树的所有节点,但查找一个节点的父节点需要遍历整棵树。
下面是使用C语言定义孩子兄弟表示法存储结构的示例代码:
#define MAX_TREE_SIZE 100
typedef struct CSNode {
int data; // 节点数据
struct CSNode* firstchild; // 指向第一个子节点的指针
struct CSNode* nextsibling; // 指向下一个兄弟节点的指针
} CSNode, *CSTree;
上述代码中,CSNode结构体表示树中的每个节点,包括节点的数据、指向第一个子节点的指针和指向下一个兄弟节点的指针。CSTree类型表示整棵树,实际上就是一个指向根节点的指针。可以根据需要调整MAX_TREE_SIZE的值来适应具体情况。与前两种存储方式不同,孩子兄弟表示法不需要额外的数组或链表来存储节点,而是直接使用节点之间的指针关系来表示树的结构。
二.并查集
1.基础认识
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。它支持两种操作:查找和合并。
在并查集中,每个元素有一个父节点,如果一个元素的父节点是自己,说明该元素是一个集合的代表元素,称之为该集合的“祖先”。通过查找该元素的祖先,可以得到该元素所属的集合。同时,如果两个元素的祖先不同,则可以将它们所属的两个集合进行合并。
并查集常见的应用场景包括图像处理、网络连通性问题、路径压缩等领域。
并查集的实现方式有多种,其中最常见的是基于数组实现的“按秩合并”和“路径压缩”算法。按秩合并指在合并两个集合时,将元素较少的集合合并到元素较多的集合中,并更新新集合的秩;路径压缩指在查找元素的祖先时,将路径上所有经过的节点都直接连接到祖先节点,以减小后续查找的复杂度。
2.说明
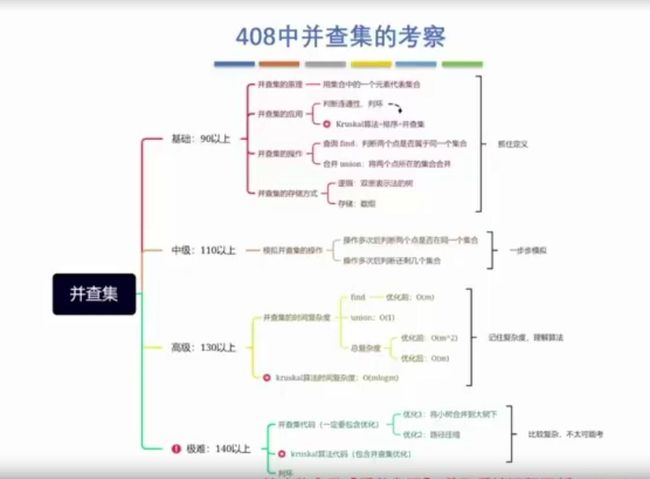
这是408考研从2022年后新增的考点,不难,但记得掌握。
这是王道考研考点要求图:
三.核心部分实现
1.定义结构体:
定义并查集结构体 首先需要定义一个并查集的结构体,包含元素个数、秩数组和父节点数组:
#include 2.初始化
初始化并查集 初始化并查集时,将每个元素的父节点指向自身:
//并查集的初始化(S即是并查集)
void Initial(int S[]){
for(int i=0;i<size;i++){ //这里初始每个元素自己就是一个集合
S[i]=-1;
high[i]=1; //初始树高设为1
}
}
3.“查”函数
查找元素的祖先节点 查找元素的祖先节点时,需要沿着父节点不断向上查找,直到找到根节点为止。
//定义“查”函数
int find1(int S[],int x){ //因为后面要写优化的find算法,这里叫find1
while(S[x]>0) //循环寻找x所在集合的根
x=S[x];
return x; //根的S[]小于0
}
4.“并”函数
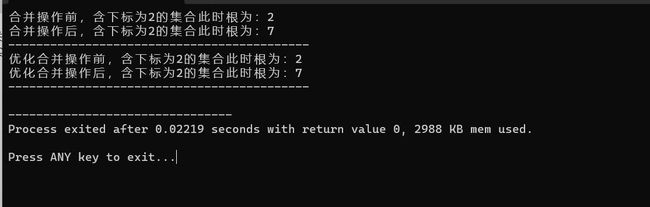
合并两个集合 合并两个集合时,可以根据秩数组的大小来判断哪个集合的根节点应该成为新集合的根节点。同时,在将新集合的根节点挂在旧集合的根节点下面时,需要更新秩数组:
//定义“并”函数
void union1(int S[],int root1,int root2){
if(root1==root2) //要求root1和root2是不同的集合
return;
S[root2]=root1; //将根root2连接到另一根root1下面
}
/*这里root1和root2的编号,你可以举个例子,比如这里root1=2,root2=3,分别代表下标为2和3的集合,
把root2的双亲定为root1,就相当于把root2连接到另一根root1下面*/
四.优化操作
1.优化原理
并查集的优化主要是通过路径压缩和按秩合并两种方法来实现的。
路径压缩是指在查找根节点的同时,将搜索路径上遇到的所有节点都直接连接到根节点,以减少下一次查找所需的时间。它可以通过递归或迭代的方式来实现。具体来说,在查找根节点时,可以沿着路径向上递归或循环查找,并将搜索路径上的所有节点直接连接到根节点。这样做可以使得后续的查找操作变得更加高效,因为每个节点都会直接连接到根节点,而不需要再重新访问路径上的其他节点。
按秩合并是指将两个集合按照它们的秩(即节点数)进行合并,从而保证较小的集合被连接在较大的集合上,进一步减少了路径压缩的深度。具体来说,当需要将两个集合合并时,先比较它们的秩大小,然后将秩较小的集合连接到秩较大的集合上。这样做可以保证较小的集合被合并到较大的集合上,从而减少了路径压缩的深度,提高了并查集的查询性能。
上面两种优化方法,分别对应着优化“查”和优化“并”操作
2.优化代码
//定义“查”的优化算法
int find(int x) {
if (x != parents[x]) {
parents[x] = find(parents[x]); //把x元素的双亲直接修改为根结点
}
return parents[x];
}
/*如果不理解可以举个例子,比如2合并到7下面,然后把3合并到2下面,这样就相当于把3合并到7的集合里,但是查早3的根结点是先找到2再找到7
如果我们在找到3的时候把3从2下面直接合并到根结点7下面,这样以后查找的时候,我们可以节省时间复杂度*/
//定义“并”的优化算法
bool union2(int x,int y){
x = find1(parents,x); //寻找 x的集合根
y = find1(parents,y); //寻找 y的集合根
if(x == y) //如果两个在同一个集合里,我们就不合并
return false;
else //否则
{
if(high[x]==high[y]) high[y]++; //如果 x的高度和 y的高度相同,则令 y的高度加1
parents[x]=y; //让 x的双亲,也就是把x合并到y集合里
}
return true;
}
五.C语言完整测试代码
#include