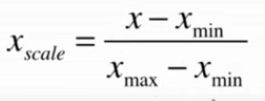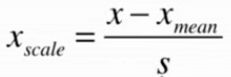【机器学习实战】数据归一化

 目录：

一、介绍

二、最值归一化

1.计算公式

2.Python实战

三、均值方差归一化

1.计算公式

2.Python实战

四、归一化要点

五、使用scikit-learn进行数据归一化

---

一、介绍

为什么需要进行数据归一化？

举个简单的例子，样本1以[1, 200]输入到模型中去的时候，由于200可能会直接忽略到1的存在。此时样本间的距离由时间所主导。

此时，如果将天数转换为占比1年的比例，200/365=0.5479, 100/365=0.2740。但也导致样本间的距离又被肿瘤大小所主导。因此有必要进行数据归一化处理。不然直接计算样本间的距离是有一定偏差的。

解决方案：

将所有的数据映射到统一尺度。

两种数据归一化的方法：

• 最值归一化（Normalization）：把所有数据映射到0-1之间。适用于分布有明显边界的情况；受outliner影响较大。
• 均值方差归一化（standardization）：把所有数据归一化到均值为0方差为1的分布中。适用于数据分布没有明显的边界；有可能存在极端的数据值。

二、最值归一化

1.计算公式

该方法实现对原始数据的等比例缩放，其中Xscale为归一化后的数据，X为原始数据，Xmax、Xmin分别为原始数据集的最大值和最小值。

2.Python实战

# 导包
import numpy as np
import matplotlib.pyplot as plt

# 随机生成0-100之间的100个数
x = np.random.randint(0, 100, size=100)
x

输出结果：

array([10, 92, 55, 25, 67, 84, 64,  2,  5, 56, 32, 37, 69, 40, 24, 86, 65,
       29, 49, 93, 13, 80, 90, 70, 80, 63, 90, 95, 25, 50, 92, 37, 42, 16,
       83, 52, 36, 14, 73,  4, 53, 84, 34, 62, 59, 50, 46, 55, 72, 43, 39,
        1, 58,  6, 84, 64, 72, 70, 41, 30, 51, 62, 79, 14, 89, 20,  7, 37,
       44, 36, 40, 89, 70, 62,  6,  3, 74, 88, 36, 90,  0, 30, 20,  6,  0,
       67, 50,  4, 36, 28, 62, 91, 94, 96, 75, 22, 19, 56, 81, 28])

# 最值归一化处理，把所有数据映射到0-1之间
(X - np.min(X)) / (np.max(X) - np.min(X))

输出结果：

array([0.10416667, 0.95833333, 0.57291667, 0.26041667, 0.69791667,
       0.875     , 0.66666667, 0.02083333, 0.05208333, 0.58333333,
       0.33333333, 0.38541667, 0.71875   , 0.41666667, 0.25      ,
       0.89583333, 0.67708333, 0.30208333, 0.51041667, 0.96875   ,
       0.13541667, 0.83333333, 0.9375    , 0.72916667, 0.83333333,
       0.65625   , 0.9375    , 0.98958333, 0.26041667, 0.52083333,
       0.95833333, 0.38541667, 0.4375    , 0.16666667, 0.86458333,
       0.54166667, 0.375     , 0.14583333, 0.76041667, 0.04166667,
       0.55208333, 0.875     , 0.35416667, 0.64583333, 0.61458333,
       0.52083333, 0.47916667, 0.57291667, 0.75      , 0.44791667,
       0.40625   , 0.01041667, 0.60416667, 0.0625    , 0.875     ,
       0.66666667, 0.75      , 0.72916667, 0.42708333, 0.3125    ,
       0.53125   , 0.64583333, 0.82291667, 0.14583333, 0.92708333,
       0.20833333, 0.07291667, 0.38541667, 0.45833333, 0.375     ,
       0.41666667, 0.92708333, 0.72916667, 0.64583333, 0.0625    ,
       0.03125   , 0.77083333, 0.91666667, 0.375     , 0.9375    ,
       0.        , 0.3125    , 0.20833333, 0.0625    , 0.        ,
       0.69791667, 0.52083333, 0.04166667, 0.375     , 0.29166667,
       0.64583333, 0.94791667, 0.97916667, 1.        , 0.78125   ,
       0.22916667, 0.19791667, 0.58333333, 0.84375   , 0.29166667])

# 随机生成0-100之间的100个数（50×2的矩阵）
X = np.random.randint(0, 100, (50, 2))

# 将整数转成浮点数
X = np.array(X, dtype=float)

# 最值归一化
X[:, 0] = (X[:, 0] - np.min(X[:, 0])) / (np.max(X[:, 0]) - np.min(X[:, 0]))
X[:, 1] = (X[:, 1] - np.min(X[:, 1])) / (np.max(X[:, 1]) - np.min(X[:, 1]))

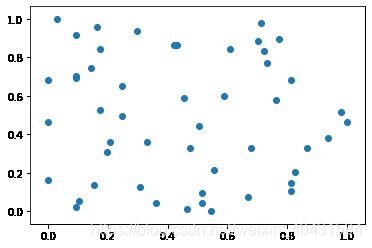
# 绘制散点图
plt.scatter(X[:, 0], X[:, 1])
plt.show()

print('第一列数据的均值为', np.mean(X[:, 0]))
print('第一列数据的方差为', np.std(X[:, 0])
print('第二列数据的均值为', np.mean(X[:, 1]))
print('第二列数据的方差为', np.std(X[:, 1]))

输出结果：

第一列数据的均值为 0.4480412371134021
第一列数据的方差为 0.29316230758866496
第二列数据的均值为 0.48494845360824745
第二列数据的方差为 0.3163383877358538

三、均值方差归一化

1.计算公式

其中，Xmean、S分别为原始数据集的均值和方差。该归一化方式要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。

2.Python实战

# 导包
import numpy as np
import matplotlib.pyplot as plt

# 随机生成0-100之间的100个数（50×2的矩阵）
X2 = np.random.randint(0, 100, (50, 2))

# 将整数转成浮点数
X2 = np.array(X2, dtype=float)

# 均值方差归一化处理
X2[:, 0] = (X2[:, 0] - np.mean(X2[:, 0])) / np.std(X2[:, 0])
X2[:, 0] = (X2[:, 1] - np.mean(X2[:, 1])) / np.std(X2[:, 1])

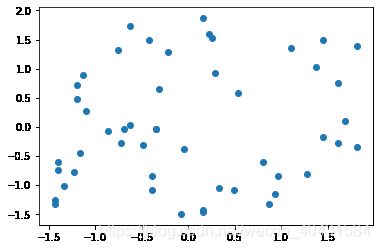
# 绘制散点图
plt.scatter(X2[:, 0], X2[:, 1])
plt.show()

print('第一列数据的均值为', np.mean(X2[:, 0]))
print('第一列数据的方差为', np.std(X2[:, 0])
print('第二列数据的均值为', np.mean(X2[:, 1]))
print('第二列数据的方差为', np.std(X2[:, 1]))

输出结果：

第一列数据的均值为 -9.325873406851315e-17
第一列数据的方差为 1.0
第二列数据的均值为 5.329070518200751e-17
第二列数据的方差为 1.0

四、归一化要点

​ 我们得到数据集训练模型之前，首先会把数据集进行切分，分成训练集和测试集，如果需要对数据进行归一化，我们可以很容易地通过训练集得到其最大值、最小值、均值和方差。但是测试集呢？如何对测试集进行数据归一化呢？

正常情况下，测试数据集是模拟真实环境的，既然是真实环境，我们就很可能无法得到所有的测试集。因此当有一个新的数据需要进行预测时，我们需要使用训练集的最大值、最小值、均值和方差对测试集数据进行归一化。

五、使用scikit-learn进行数据归一化

本案例采用鸢尾花数据集进行测试。

# 导包
import numpy as np
from sklearn import datasets 

# 加载iris数据集
iris = datasets.load_iris()

X = iris.data
y = iris.target

# 将数据集分成训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 666)

# 导入StandardScaler包（进行均值方差归一化）
from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()

# 训练
standardScaler.fit(X_train)

print(standardScaler.mean_)   # 均值 四个特征的均值
print(standardScaler.scale_)  # 分布范围

输出结果：

array([5.83416667, 3.08666667, 3.70833333, 1.17      ])
array([0.81019502, 0.44327067, 1.76401924, 0.75317107])

# 归一化处理
X_train = standardScaler.transform(X_train) 
X_test_standard = standardScaler.transform(X_test)
X_test_standard

输出结果：

array([[-0.28902506, -0.19551636,  0.44878573,  0.43814747],
       [-0.04217092, -0.64670795,  0.78891808,  1.63309511],
       [-1.0295875 , -1.77468693, -0.23147896, -0.22571233],
       [-0.04217092, -0.87230374,  0.78891808,  0.96923531],
       [-1.52329579,  0.03007944, -1.25187599, -1.28788802],
       [-0.41245214, -1.32349533,  0.16534211,  0.17260355],
       [-0.16559799, -0.64670795,  0.44878573,  0.17260355],
       [ 0.82181859, -0.19551636,  0.8456068 ,  1.10200727],
       [ 0.57496445, -1.77468693,  0.39209701,  0.17260355],
       [-0.41245214, -1.09789954,  0.39209701,  0.03983159],
       [ 1.06867274,  0.03007944,  0.39209701,  0.30537551],
       [-1.64672287, -1.77468693, -1.36525344, -1.15511606],
       [-1.27644165,  0.03007944, -1.19518726, -1.28788802],
       [-0.53587921,  0.70686683, -1.25187599, -1.0223441 ],
       [ 1.68580811,  1.15805842,  1.35580532,  1.76586707],
       [-0.04217092, -0.87230374,  0.22203084, -0.22571233],
       [-1.52329579,  1.15805842, -1.53531961, -1.28788802],
       [ 1.68580811,  0.25567524,  1.29911659,  0.83646335],
       [ 1.31552689,  0.03007944,  0.78891808,  1.50032315],
       [ 0.69839152, -0.87230374,  0.90229552,  0.96923531],
       [ 0.57496445,  0.48127103,  0.56216318,  0.57091943],
       [-1.0295875 ,  0.70686683, -1.25187599, -1.28788802],
       [ 2.30294347, -1.09789954,  1.80931511,  1.50032315],
       [-1.0295875 ,  0.48127103, -1.30856471, -1.28788802],
       [ 0.45153738, -0.42111215,  0.33540828,  0.17260355],
       [ 0.08125616, -0.19551636,  0.27871956,  0.43814747],
       [-1.0295875 ,  0.25567524, -1.42194216, -1.28788802],
       [-0.41245214, -1.77468693,  0.16534211,  0.17260355],
       [ 0.57496445,  0.48127103,  1.29911659,  1.76586707],
       [ 2.30294347, -0.19551636,  1.35580532,  1.50032315]])

# 导包，测试数据归一化之后KNN的性能
from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier(n_neighbors = 3)
knn_clf.fit(X_train, y_train)

# 计算准确度
knn_clf.score(X_test_standard, y_test) 

输出结果：

1.0

如果训练集进行了归一化，测试集不做归一化？结果又会如何？

knn_clf.score(X_test, y_test)

输出结果：

0.3333333333333333

---

菜鸟还在学习ing！

后续，如有学习其他数据归一化处理方法，继续补充！