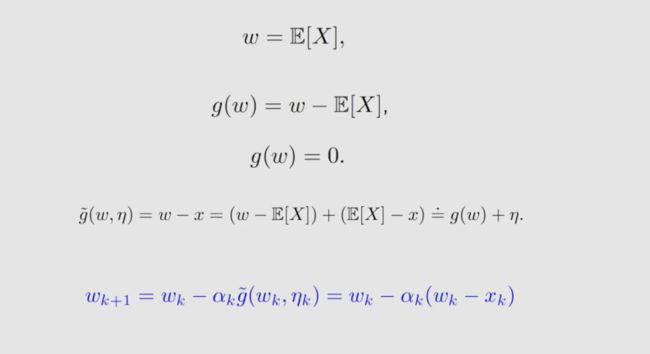强化学习:时序差分算法 TD-learning
例子引入
首先,我们考虑简单的平均估计计算: w = E [ X ] w=E[X] w=E[X],根据 RM算法 计算过程如下:
接着上面的例子,我们现在考虑一个较为复杂的问题,估计函数 v ( X ) v(X) v(X) 的平均值,根据 RM算法 计算过程如下:
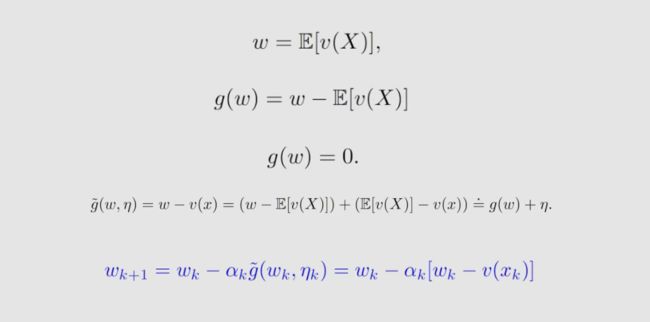
接着上面的例子,我们现在考虑一个更复杂的问题,有两个随机变量,根据 RM算法 计算过程如下:

TD 算法介绍
TD-Learning 通常指的是广泛的一类RL算法,但此处的 TD-Learning 是指一种特定的算法:状态估计算。
TD算法是基于数据的,也就是说它不基于模型来实现强化学习的。那它要的数据是什么呢?是遵循给定的策略 π π π 产生的,形式可以为一长串 ( s 0 , r 1 , s 1 . . . . , s t , r t + 1 , s t + 1 . . . ) (s_0,r_1,s_1....,s_{t},r_{t+1},s_{t+1}...) (s0,r1,s1....,st,rt+1,st+1...) 或者写成集合 { ( s t , r t + 1 , s t + 1 ) } t {\{(s_{t},r_{t+1},s_{t+1})\}}_t {(st,rt+1,st+1)}t,TD算法是用这些数据来估计这个策略 π π π 所对应的 state value,如下:

其中 t = 0 , 1 , 2 , . . . t = 0,1,2,... t=0,1,2,... , v t ( s t ) v_t(s_t) vt(st) 是策略 π π π 下 状态 s t s_t st 的状态估计值; α t ( s t ) \alpha_t (s_t) αt(st)是时间 t t t 时刻 s t s_t st 的学习率。在 t t t 时刻,只有访问的状态 s t s_t st 的值被更新,而未访问的状态 s t s_t st 的值保持不变。
为什么 v ˉ t \bar v_t vˉt 被称为 TD target ?这是因为 TD 算法将是将 v ( s t ) v(s_t) v(st) 朝着 v ˉ t \bar v_t vˉt 改进,数学证明如下:
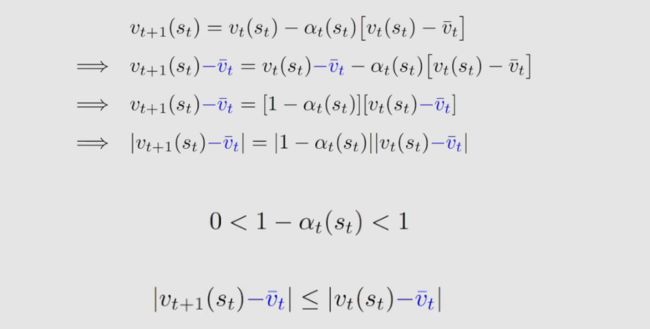
那么,TD error 是什么?两个相续时间变量的差值,这也是被叫做 时序差分算法 的原因,它实际反映了 v t v_t vt 与 v π v_π vπ 之间的误差,数学证明如下:
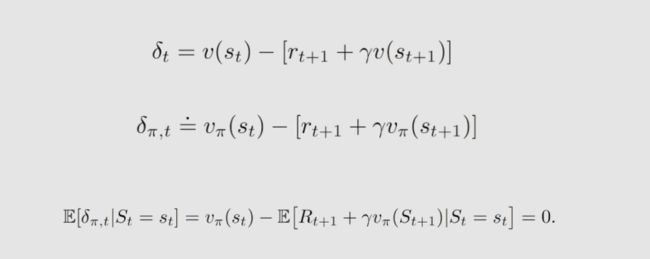
如果 v t = v π v_t = v_π vt=vπ,则 δ t δ_t δt应该为零(在期望意义上);因此,如果 s t s_t st 不为零,则 v t ≠ v π v_t≠v_π vt=vπ。TD error 可以解释为新息,也就是从经验 ( s t , r t + 1 , s t + 1 ) (s_t,r_{t+1},s_{t+1}) (st,rt+1,st+1)中获得的新信息。
.
我们可以知道 TD算法仅估计给定策略的状态值,它不能估计动作值,也不能搜索最优策略,TD算法对于理解强化学习的核心思想至关重要。那么,TD算法从数学上做了什么?它求解给定策略 π π π 的 Bellman 方程。
首先,我们引入一个新的贝尔曼公式,并用 RM 算法求解,如下:
可以发现,上述式子中RM 算法求解贝尔曼方程得到的式子与 TD 算法的式子相似,但有两个不同点值得特别注意,第一要反复采样得到集合 { ( s , r , s ′ ) } {\{(s,r,s')}\} {(s,r,s′)}, k = 1 , 2 , 3 , … … k=1,2,3,…… k=1,2,3,……;第二,认为 v π ( s ′ ) v_π(s') vπ(s′) 是已知的。 消除两个不同点的方法如下:1、将 { ( s , r , s ′ ) } {\{(s,r,s')}\} {(s,r,s′)} 改为 { ( s t , r t + 1 , s t + 1 ) } {\{(s_t,r_{t+1},s_{t+1})}\} {(st,rt+1,st+1)} ,因为等式右边 v π v_π vπ没办法很好估计,这样就只有通过一个 episode 循环迭代,即访问就更新不访问不更新。第二,用状态 s ′ s' s′ 的估计值 v k ( s ′ ) v_k(s') vk(s′) 取代 v π ( s ′ ) v_π(s') vπ(s′) 。
.
Saesa 算法
TD算法只能估计状态值而不能估计动作值,Sarsa算法是一种可以直接估计动作值的算法,我们来看看如何使用Sarsa来寻找最优策略。
首先,我们要估计给定策略 π π π 下的动作值。假设我们有一些经验数据 { ( s t , a t , r t + 1 , s t + 1 , a t + 1 ) } t {\{(s_t, a_t,r_{t+1},s_{t+1},a_{t+1})}\}_t {(st,at,rt+1,st+1,at+1)}t,那么可以使用以下的Sarsa算法来估计动作值:
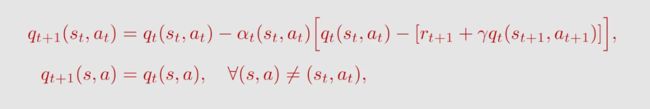
q t ( s t , a t ) q_t(s_t,a_t) qt(st,at) 是对 q π ( s t , a t ) q_π(s_t, a_t) qπ(st,at) 的估计; α t ( s t , a t ) \alpha_t(s_t,a_t) αt(st,at) 是学习率,它取决于 s t s_t st 和 a t a_t at 。
我们可以发现,Sarsa是用动作值估计 q ( s , a ) q(s,a) q(s,a) 替换TD算法中的状态值估计 v ( s ) v(s) v(s) ,Sarsa通过估计值函数来更新策略。因此,我们可以简单理解为 Sarsa是TD算法的动作值版本。与TD算法类似,不同之处在于,在Sarsa算法中,我们关注的是动作值函数 q ( s , a ) q(s,a) q(s,a),而不是状态值函数 v ( s ) v(s) v(s)。Sarsa通过估计和更新动作值函数来学习最优策略。具体而言,Sarsa在每个时间步中观察到当前状态和动作,然后执行该动作并观察到奖励和下一个状态。然后,它使用新的观测值来更新动作值函数,以逐步改进对最优动作值的估计。因此,Sarsa是基于TD算法的一种变体,通过将状态值估计替换为动作值估计,使其成为一种动作值版本的TD算法。
RL的最终目标是找到最优策略。要做到这一点,我们可以将Sarsa与 策略优化 结合,这种组合算法也称为Sarsa。

这个算法在更新 q ( s t , a t ) q(s_t, a_t) q(st,at) 之后,会立即更新 s t s_t st 的策略, 策略更新采用 ε − g r e e d y ε-greedy ε−greedy 策略,以平衡利用和探索,这个核心思想是使用算法来解决给定策略的贝尔曼方程。
Expected Sarsa
在 Expected Sarsa 算法中,是将 Sarsa 算法的 r t + 1 + γ q t ( s t + 1 , a t + 1 ) ] r_{t+1} + γq_t(s_{t+1},a_{t+1})] rt+1+γqt(st+1,at+1)] 替换成 r t + 1 + γ E [ q t ( s t + 1 , A ) ] r_{t+1} + γE[q_t(s_{t+1},A)] rt+1+γE[qt(st+1,A)],其中 γ γ γ 是折扣因子, q t ( s t + 1 , a t + 1 ) q_t(s_{t+1},a_{t+1}) qt(st+1,at+1) 是根据当前策略 π π π 在下一个状态 s t + 1 s_{t+1} st+1 和动作 a t + 1 a_{t+1} at+1 的动作值估计,而在 Expected Sarsa 算法 E [ q t ( s t + 1 , A ) ] E[q_t(s_{t+1},A)] E[qt(st+1,A)] 是根据当前策略 π π π 在下一个状态 s t + 1 s_{t+1} st+1 和所有可能的动作 A A A 的动作值的期望。
换句话说,Expected Sarsa算法通过对下一个状态的所有可能动作的动作值进行期望,来计算 TD target,而不是像Sarsa算法那样只考虑下一个状态和选择的动作的动作值。这种改变使 Expected Sarsa 算法更加稳定,因为它对不同动作的期望值进行了考虑,而不仅仅是选择一个动作的值。这可以减少由于不精确的动作值估计而导致的波动性,并提供更准确的 TD target .
相对于Sarsa算法,Expected Sarsa算法需要更多的计算,因为随机变量减少了,随机变量从 ( s t , a t , r t + 1 , s t + 1 , a t + 1 ) (s_t, a_t,r_{t+1},s_{t+1},a_{t+1}) (st,at,rt+1,st+1,at+1) 到 ( s t , a t , r t + 1 , s t + 1 ) (s_t, a_t,r_{t+1},s_{t+1}) (st,at,rt+1,st+1) ,Expected Sarsa算法考虑了所有可能的动作的期望值,它将 a t + 1 a_{t+1} at+1 从随机变量中移除。这样一来,估计值中的随机性减少了,因为不再依赖于选择的下一个动作的随机性。这种减少随机变量的做法有助于降低估计方差,使算法更加稳定。通过减少随机性的影响,Expected Sarsa可以提供更可靠和准确的动作值估计,从而改善学习过程。
.
n-step Sarsa
n-step Sarsa,是 Sarsa 与 MC 结合的算法,数学推导如下:

我们很容易知道 n-step Sarsa 需要的数据有 ( s t , a t , r t + 1 , s t + 1 , a t + 1 , . . . , r t + n , s t + n , a t + n ) (s_t,a_t, r_{t+1},s_{t+1},a_{t+1},...,r_{t+n}, s_{t+n},a_{t+n}) (st,at,rt+1,st+1,at+1,...,rt+n,st+n,at+n) ,这样面临一个问题就是 由于在时间步 t t t 时尚未收集到 ( r t + n , s t + n ; a t + n ) (r_{t+n}, s_{t+n}; a_{t+n}) (rt+n,st+n;at+n) 的信息,我们无法在步骤 t t t 中实现 n-step Sarsa,所以要等到时间步 t + n t + n t+n 才来更新 ( s t , a t ) (s_t, a_t) (st,at) 的动作值.
q t + n ( s t , a t ) = q t + n − 1 ( s t , a t ) − α t + n − 1 ( s t , a t ) [ q t + n − 1 ( s t , a t ) − [ r t + 1 , γ r t + 2 + . . . + γ n q t + n − 1 ( s t + n , a t + n ) ] ] q_{t+n}(s_t,a_t)=q_{t+n-1}(s_t,a_t)-\alpha_{t+n-1}(s_t,a_t)[q_{t+n-1}(s_t,a_t)-[r_{t+1},γr_{t+2}+...+γ^nq_{t+n-1}(s_{t+n},a_{t+n})]] qt+n(st,at)=qt+n−1(st,at)−αt+n−1(st,at)[qt+n−1(st,at)−[rt+1,γrt+2+...+γnqt+n−1(st+n,at+n)]]
在n-step Sarsa算法中,我们需要等待n个时间步才能计算并更新 ( s t , a t ) (s_t, a_t) (st,at) 的动作值,通过等待 n n n 个时间步来更新动作值,n-step Sarsa 算法能够更准确地估计动作值函数,并在学习过程中利用更长的时间序列信息。这有助于提高算法的性能和学习效果。由于n-step Sarsa包含了Sarsa和MC学习作为两种极端情况,它的性能是Sarsa和MC学习的综合体:当 n n n 较大时,其性能接近MC学习,因此具有较大的方差但较小的偏差;当 n n n 较小时,其性能接近Sarsa,因此由于初始猜测的存在具有相对较低的方差,相对较大的偏差。综上所述,n-step Sarsa是在Sarsa和MC学习之间取得平衡的一种方法。通过调整n的值,我们可以在偏差和方差之间进行权衡,从而获得更适合特定问题的性能表现。此外,n-step Sarsa还可以用于评估策略的价值,并与策略改进一起使用来搜索最优策略。
.
Q-learning
Q-learning 是最常用的强化学习算法之一,Sarsa可以估计给定策略下的动作值函数,但它必须与策略改进步骤结合使用才能找到最优策略,而 Q-learning 可以直接估计最优动作值函数,从而找到最优策略。其数学表达式如下:

通过上面式子我们知道 Q-learning 和 Sarsa非常相似,它们的区别仅在于 TD target 的计算方式:
Q-learning 中的 TD target 为 r t + 1 + γ m a x a ∈ A q t ( s t + 1 , a ) r_{t+1} + γ max_{a∈A} q_t(s_{t+1}, a) rt+1+γmaxa∈Aqt(st+1,a)。
Sarsa中的 TD target 为 r t + 1 + γ q ( s t + 1 , a t + 1 ) r_{t+1} + γq_(s_{t+1}, a_{t+1}) rt+1+γq(st+1,at+1)。
在Q-learning中,TD target 采用了对下一个状态 s t + 1 s_{t+1} st+1 的所有可能动作 a a a 的最大动作值函数。这意味着 Q-learning 在更新 Q 值时,考虑了在下一个状态中选择最优动作的情况。而在Sarsa中,TD target 采用了在下一个状态 s t + 1 s_{t+1} st+1 中根据当前策略选择的动作 a t + 1 a_{t+1} at+1 的动作值函数。这意味着Sarsa 在更新 Q 值时,是根据当前策略在下一个状态中选择了一个动作进行更新。因此,Q-learning 和 Sarsa在 TD target 的计算方式上有所不同,这也导致了它们在算法行为和性能上的差异。
Q-learning 在数学上求解的是一个 贝尔曼最优方程:
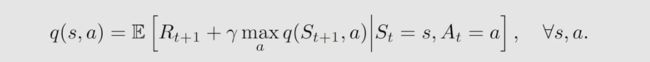
在进一步学习Q学习之前,我们首先介绍两个重要的概念:on-policy 和 off-policy 。在 TD 算法中存在两种策略:
行为策略(behavior policy):用于生成经验样本。
目标策略(target policy):不断更新以朝向最优策略。
当行为策略与目标策略相同时,称为on-policy;当它们不同时,称为 off-policy
off-policy 可以使用其他策略生成的经验样本来搜索最优策略,行为策略可以选择为具有探索性质。例如,如果我们希望估计所有 状态-动作 的动作值,我们可以使用一个具有探索性质的策略生成足够多次访问每个 状态-动作 的轨迹。
如何判断一个TD算法是 on-policy 还是 off-policy?
首先,看算法在数学上是解决贝尔曼公式,还是是贝尔曼最优公式
其次,看实现该算法所需的条件
现在,我们来判断之前学的算法是 on-policy 还是 off-policy, 第一个我们来判断Sarsa,第二个判断基于蒙特卡洛的方法,第三个判断Q-learning
Sarsa是一个on-policy算法。
首先,在数学上 Sarsa 是在求解给定策略 π π π 的贝尔曼方程:
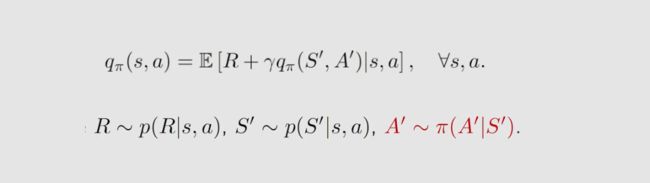
其次,看实现 Sarsa 算法所需的变量条件 :
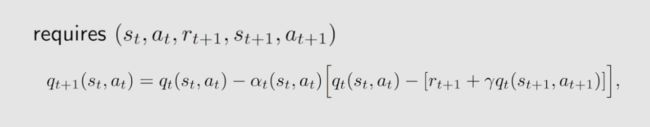
Sarsa 算法中,如果给定了 ( s t , a t ) (s_t,a_t) (st,at),那么 r t + 1 r_{t+1} rt+1 和 s t + 1 s_{t+1} st+1 并不依赖于任何策略, a t + 1 a_{t+1} at+1 是遵循策略 π t ( s t + 1 ) π_t(s_{t+1}) πt(st+1) 生成的,可以知道策略 π t π_t πt 既是目标策略又是行为策略。
.
MC 是一个on-policy算法。
首先,在数学上 MC 是通过给定的策略 π π π 采样计算 q ( s , a ) q(s,a) q(s,a)
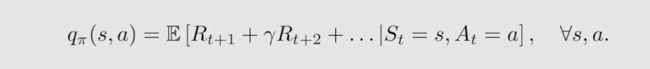
其次,mc方法的实现是
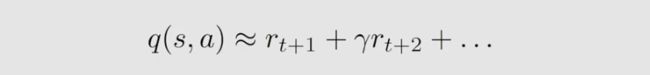
策略用于生成样本,这些样本进一步用于估计策略的动作值。基于动作值,我们可以改进策略。
.
Q-learning 是一个off-policy算法。
首先,Q-learning 的目的是求解贝尔曼最优性方程:

其次,看实现 Q-learning 算法所需的变量条件 :
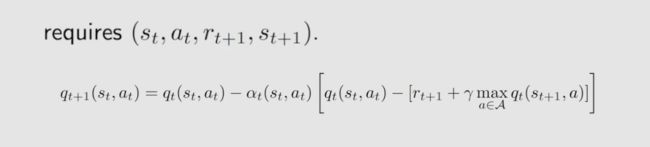
Q-learning 算法的 on-policy 的 version,如下:
Q-learning 算法的 off-policy 的version,如下:

TD 算法总结
上述的所有的 TD 算法都可以用这样一个统一的表达式给表达出来:
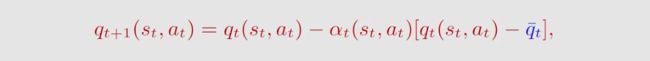
q ˉ t \bar q_t qˉt 是 TD target.

通过设置 α t ( s t , a t ) = 1 \alpha _t(s_t,a_t) = 1 αt(st,at)=1,可以将MC方法表达为上述统一表达式,因此 q t + 1 ( s t , a t ) = q ˉ t q_{t+1}(s_t,a_t) = \bar q_t qt+1(st,at)=qˉt。
.