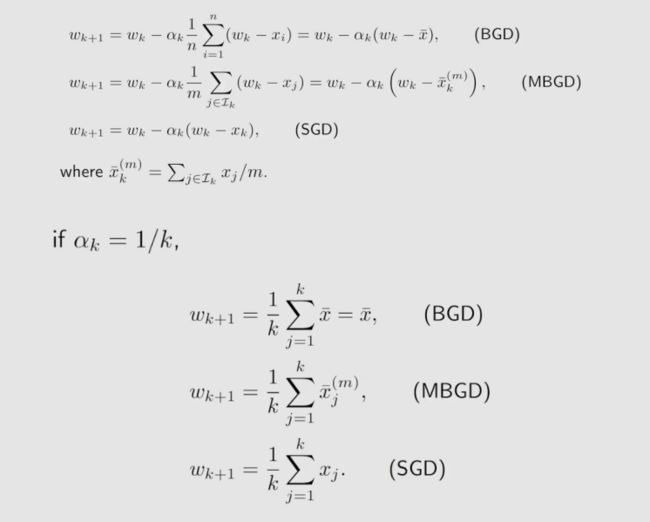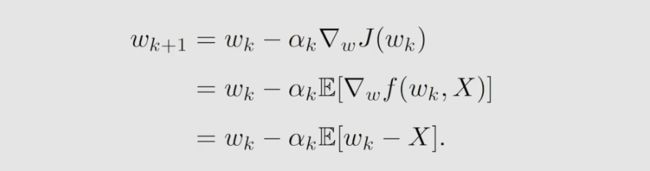强化学习:随机近似与随机梯度下降
mean estimation
通过前面的学习,我们知道可以通过很多采样来求期望。而求 x ˉ \bar x xˉ 的方法由两种,一是直接将采样数据相加再除以个数,但这样的方法运行效率较低。

第二种方法是迭代式的计算,即来几个数据就算几个数据,具体计算如下:

随机近似法:Robbins-Monro(RM)
假设我们现在需要求解方程:
g ( w ) = 0 g(w)=0 g(w)=0
那么就有两种情况,一种是函数表达式我们知道,而另一种是表达式我们不知道。表达式不知道,怎么求解呢?实际上,RM 算法可以求解。下面,以求解方程为例,我们来学习 RM 算法,RM 算法是一种迭代算法。

其中, a k a_k ak 是一个正系数。 { w k } {\{w_k}\} {wk} 是输入序列, g ~ { w k , η k } \widetilde{g}{\{w_k,\eta _k}\} g {wk,ηk} 是输出序列。为了方便理解,我们给出一个具体的例子:
g ( w ) = t a n h ( w − 1 ) g(w)=tanh(w-1) g(w)=tanh(w−1)
我们知道 g ( w ) g(w) g(w) 的真实解 w ∗ w^* w∗=1,给定初始值 w 1 w_1 w1=3, a k = 1 / k a_k=1/k ak=1/k, η k = 0 \eta _k=0 ηk=0,计算得到的结果 w ∗ = 1 w^*=1 w∗=1 如下:
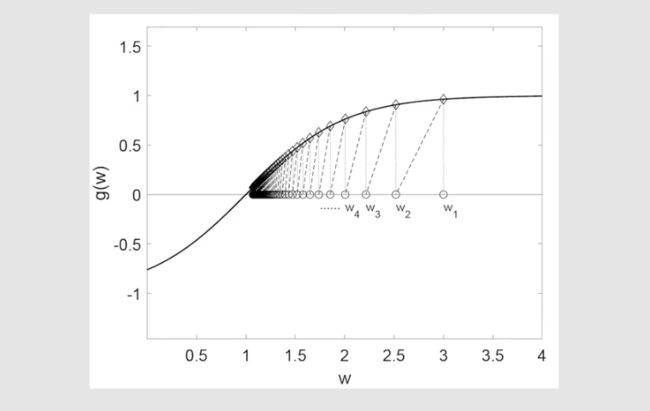
RM算法:收敛性分析
上面的分析是直观的,并不严格,现在我们给出下列数学严格的收敛条件。

条件一:表明要求函数 g g g 是一个递增函数,其梯度是有界的。
条件二:关于系数 a k a_k ak
a k a_k ak 的和应该等于无穷,为什么?我们将 MR 算法分别写出来,在相加可以得到如下式子:
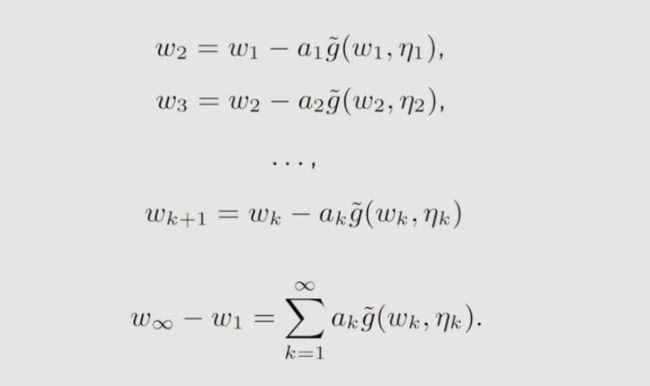
表明,如果 a k a_k ak 的和小于无穷,那么 a k g ~ ( w k , η k ) a_k\widetilde{g}{(w_k,\eta _k)} akg (wk,ηk) 的和是有界的,则说明 w 1 w_1 w1 不能随便定,而 a k a_k ak 的和等于无穷,使得我们可以放心选用初始值 w 1 w_1 w1 。
a k 2 a_k^2 ak2 的和应该小于无穷,表明 a k a_k ak一定会收敛到0,为什么呢?
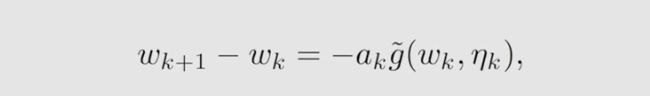
可知,如果 a k a_k ak 趋近于0,那么就有 a k g ~ ( w k , η k ) a_k\widetilde{g}{(w_k,\eta _k)} akg (wk,ηk) 趋近于0,即有 w k + 1 − w k w_{k+1}-w_k wk+1−wk趋近于0。
我们会发现在许多强化学习算法中,通常会选择 a k a_k ak 作为一个足够小的常数,因为 1/k 会越来越小导致算法效率较低 。尽管在这种情况下第二个条件没有被满足,但算法仍然可以有效地工作,因为实际迭代的次数是有限。
条件三:关于系数 η \eta η,表明 η \eta η 的期望为0,方差有界。
随机梯度下降法:SGD
随机梯度下降(SGD)算法 广泛应用于机器学习领域和RL领域,SGD是一种特殊的RM算法,而均值估计算法是一种特殊的SGD算法。
假设我们目的是求解优化问题,有方程:

w w w 是要优化的参数。 X X X 是一个随机变量。期望是关于X的。其中 w w w 和 X X X 既可以是标量,也可以是向量。函数 f ( . ) f(.) f(.) 是标量。
现在,我们的目标是要找到最优的 w w w 使得目标函数达到最小。求解的方法有三种:
梯度下降(GD)
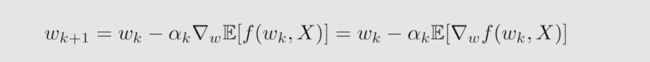
GD 算法思路就是沿着梯度的方向去进行下降找到最小值,从而使得到的解逼近真实值 w ∗ w^* w∗ , a k a_k ak 为步长,控制下降的速度。其特点是要知道函数梯度,如果不知道梯度函数怎么求解呢?
批量梯度下降(BGD)
批量梯度下降法是利用数据来避免求解梯度函数。通过大量采样,最后用平均值来近似代替梯度函数的期望,如下:
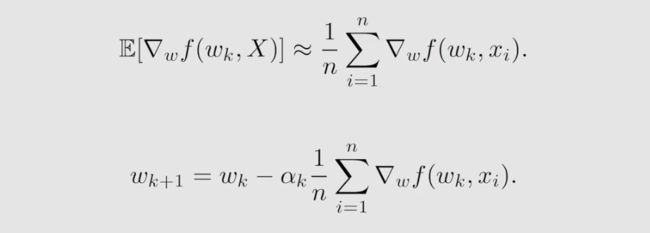
但存在的问题是,对于每个 w k w_k wk 都需要采样许多样本。
随机梯度下降法(SGD)

随机梯度下降法与梯度下降法相比:用 ▽ k f ( w k , x k ) ▽_kf(w_k,x_k) ▽kf(wk,xk)取代真实梯度 E [ ▽ k f ( w k , x k ) ] E[▽_kf(w_k,x_k)] E[▽kf(wk,xk)],与批处理梯度下降法相比,n=1,即只采样一次。
.
我们考虑这样一个优化例子:

我们知道 优化的解 w ∗ = E [ X ] w^*=E[X] w∗=E[X],我们知道 J ( m ) J(m) J(m) 要达到最小值,它的一个必要条件是 ▽ J ( w ) = 0 ▽J(w)=0 ▽J(w)=0 ,可以得到 w ∗ = E [ X ] w^*=E[X] w∗=E[X]
SGD算法:收敛性分析
SGD的一个基本思路就是从 GD 到 SGD ,因为 E 是不知道的,所以干脆就把 E 给去掉,然后用一个采样来近似代替这个 E,用随机梯度代替真实梯度,这就是SGD。我们很容易知道,它们之间肯定是存在误差,如下:

存在误差的种情况下,用SGD是否能够找到最优的那个解呢?答案是肯定的,那么为什么呢?实际上,SG是一个特殊的RM算法。证明如下:
SGD要解决问题是去优化求解这样一个方程,我们可以将这个优化问题转换成一个求解方程 g ( w ) g(w) g(w) 的问题,然后就用 RM 算法求解。所以说SGD算法实际上是求解解方程 g ( w ) g(w) g(w) 根的特殊问题的一个RM算法。
因为SGD是一个特殊的RM算法,那么前面RM算法的收敛性就可以应用到SGD的收敛性分析当中。

SGD算法的性质
SGD是用随机梯度代替真实梯度,而随机梯度具有随机性,那会不会造成 SGD 收敛的随机性也比较大?为回答这个问题,用相对误差来分析随机和批处理梯度两者之间,利用拉格朗日中值定理得到如下式子:

我们假设 f f f 的二阶梯度是一个正数
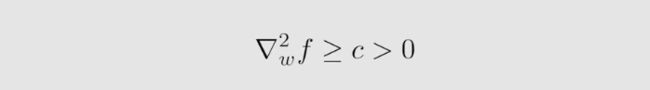
得到以下推式:

根据上述方程,我们可以得到 SGD 的一个有趣的收敛性质。 相对误差 δ k δ_k δk与 ∣ w k − w ∗ ∣ |w_k - w^*| ∣wk−w∗∣成反比;当 ∣ w k − w ∗ ∣ |w_k - w^*| ∣wk−w∗∣ 较大时,得到的相对误差 δ k δ_k δk 较小,SGD 类似于 GD 。当 w k w_k wk 接近 w ∗ w^* w∗时,相对误差 δ k δ_k δk 可能较大,并且在 w ∗ w^* w∗ 附近的收敛表现出更多的随机性。
.
现在,我们以一个例子来理解这个性质。 X ∈ R 2 X∈R^2 X∈R2 表示平面上的一个随机位置。其分布在以原点为中心、边长为20的正方形区域内均匀分布,现在随机采样100个样本 { x i } i = 0 100 {\{x_i}\}_{i=0}^{100} {xi}i=0100,其真实均值为 E[X] = 0,现在我们用上述算法进行均值估计计算,结果如下:

可以发现,当均值的初始猜测与真实值相差较远,SGD估计可以快速接近真实值的邻域,尽管当估计接近真实值时,它表现出一定的随机性,但仍然逐渐接近真实值。
.
我们可能会经常会遇到一种确定性的SGD公式,没有涉及任何随机变量,这样的问题怎么求解呢?如下图:

f ( w , x i ) f(w, x_i) f(w,xi) 是一个参数化函数, w w w 是要优化的参数。
{ x i } i = 0 n {\{x_i}\}_{i=0}^{n} {xi}i=0n 是一组实数,其中 x i x_i xi 不是任何随机变量的样本。
.
那么,我们能不能用 SGD 算法进行求解呢?我们用其平均值 x k x_k xk 来代替求平均的过程,得到的式子与 SGD 非常相似,但不同的是其中没有涉及随机变量。为了可以使用 SGD 算法,我们手动引入随机变量,我们就引入一个随机变量 X X X , X X X 是定义在集合 { x i } i = 0 n {\{x_i}\}_{i=0}^{n} {xi}i=0n 上的, x i x_i xi 服从均匀分布,每个被取到的概率都是 1 / n 1/n 1/n 。这样我们就转换成了 E [ f ( w , X ) ] E[f(w,X)] E[f(w,X)],求解这个问题自然也就是 SGD 算法。如下:

对比:BGD、MBGD、SGD
假设我们想要最小化 J ( w ) = E [ f ( w , X ) ] J(w) = E[f(w,X)] J(w)=E[f(w,X)],给定一组随机样本 { x i } i = 0 n {\{x_i\}_{i=0}^n} {xi}i=0n。分别用批量梯度下降(BGD)、随机梯度下降(SGD)和小批量梯度下降(MBGD)解决这个问题。
在BGD算法中,所有样本在每次迭代中都被使用。当 n n n 很大时, ( 1 / n ) ∗ Σ i = 1 n ▽ w f ( w k , x i ) (1/n) * Σ_{i=1}^n▽wf(w_k,x_i) (1/n)∗Σi=1n▽wf(wk,xi) 接近真实梯度 E [ ▽ w f ( w k , x i ) ] E[▽wf(w_k,x_i)] E[▽wf(wk,xi)]。
在MBGD算法中, I k I_k Ik是 1 , . . , n {1,..,n} 1,..,n 的一个子集,其大小为 ∣ I k ∣ = m |I_k| = m ∣Ik∣=m,集合 I k I_k Ik通过 m m m 次独立采样得到。
在SGD算法中, x k x_k xk 是从 { x i } i = 0 n {\{x_i\}_{i=0}^n} {xi}i=0n中随机采样得到的。
总结:
一定程度上,MGBD 包括了 BGD 与 SGD 。当 m = 1 m=1 m=1 时就变成了SGD ,当 m m m 较大时不完全变成 BGD 因为MBGD使用的是随机获取的n个样本,而BGD使用所有n个样本,其中MBGD可能多次使用同一个值,而BGD只使用每个数字一次。相比与SGD,MBGD具有较少的随机性,因为它使用更多的样本,而不仅仅是SGD中的一个样本;与BGD相比,MBGD不需要在每次迭代中使用所有样本,使其更加灵活和高效。
案例
在给定的 x i {x_i} xi,我们的目标是计算均值 ( 1 / n ) ∗ Σ i = 1 n ∣ ∣ w − x i ∣ ∣ (1/n) * Σ_{i=1}^n||w-x_i|| (1/n)∗Σi=1n∣∣w−xi∣∣。这个问题可以等价地表述为以下优化问题: