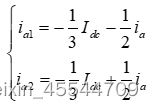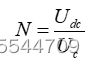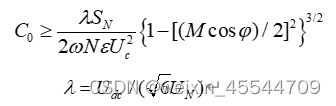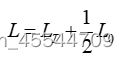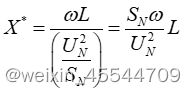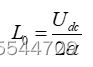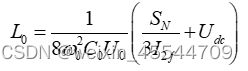基于simulink搭建的模块化多电平MMC仿真模型

1.   模块化多电平换流器的运行原理                                                                                                 1.1模块化多电平换流器的拓扑结构

       MMC共由6个桥臂构成。其中每个桥臂由若干个串联且结构相同的子模块(Sub-Module, SM)与一个电抗器L串联构成，上下两个桥臂构成一个相单元，如图 1‑1所示。出于模块化设计和制造的目的,6个桥臂具有对称性,即各子模块内部元件参数和各桥臂电抗值都是相同的。与以往的电压源换流器拓扑结构显著不同的是,MMC在直流侧正负极之间没有直流储能电容。

 图1-1 MMC拓扑结构

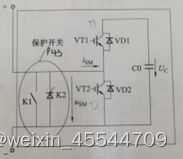
       MMC的子模块由一个作为开关单元的IGBT半桥和一个直流储能电容构成,如图 1‑2所示。为子模块的端口输出电压，为该子模块所在桥臂的电流，Uc为子模块的电容电压，每个子模块都是两端元件,通过两个开关单元[将IGBT(以VT1代表)及相应的反并联二极管VD1组成的整体定义为开关单元,简称T1, T2的意义类推,可以同时在两种电流方向的情况下进行电容电压Uc与0之间的切换。

 图 1‑2 子模块结构图

       K1是一个可靠的高速旁路开关,能保证子模块发生故障的时候将故障子模块快速旁路，从而能保证桥臂电流的连续性。K2是一个压接式封装晶闸管，具有良好的承受冲击电流的能力，当发生诸如换流器直流母线短路或传输线短路这类严重的故障时,K2能保护与它并联的续流二极管。由此可知,K1 和K2的设置增强了MMC的安全性和实用性。

1.2 模块化多电平换流器的工作机制

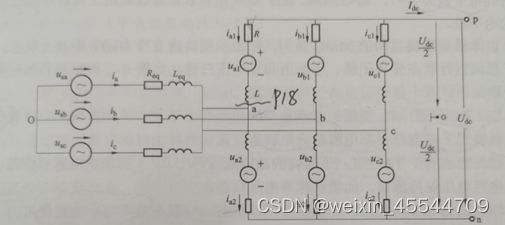
       图1-3为MMC的等效电路图。其中p和n表示换流器的直流侧的正负极，他们相对于参考中性点O的电压分别为Udc/2和- Udc/2，换流器中三个相单元具有严格的对称性，每一相桥臂可通过子模块的投切控制桥臂输出电压，故每相桥臂均可等效为一个可控电压源，以a相为例，忽略桥臂等效电阻R以及桥臂电抗器L的电压降，可得

 图 1‑3 模块化多电平换流器等效电路

                                                    (1-1)

将式(1-1)中的两式相加可以得到

                                                         (1-2)

        将上述两式可以得到，MMC正常运行时每相单元中出于投入状态的子模块数在任意时刻都相等且保持不变，通过对每相上、下桥臂中处于投入状态的子模块数进行分配来实现换流器交流侧输出多电平电压波形的目的。

      由于MMC中三个相单元具有严格的对称性，相单元中的上、下桥臂也具有严格的对称性，因此直流电流Idc在三个相单元间均分，a相的输出端电流在上、下桥臂均分为两部分。因此，再不计相间环流时，可以得到a相上、下桥臂电流为

                                                       (1-3)

根据上述原理，当a相上桥臂中所有子模块都切除时ua1=0，这时a相下桥臂所有的子模块都要投入，才能得到直流电压。又因为相单元中处于投入状态的子模块是一个不变的量，所以一般情况下,每个相单元中处于投入状态的子模块数为N个,是该相单元中全部子模块数2N的一半(不考虑冗余)。这样单个桥臂处于投入状态的子模块数可以是0.1,2.….N.也就是说MMC最多能输出的电平数为N+1,这与MMC的扩展性相一致,可以通过子模块串联达到很高的电平数。

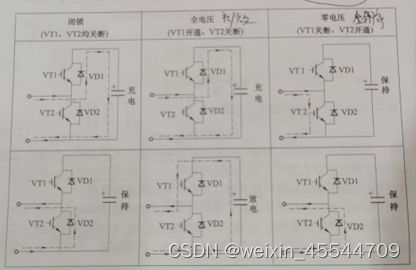
      以半桥子模块结构的MMC为例,根据子模块内2个IGBT的开关状态,可将子模块运行状态分为闭锁、全电压和零电压三种,如图1-4所示,具体三种状态分析如下

（1）TI导通，T2关断：子模块端口电压等于子模块中电容电压,桥臂电流的方向决定了见容处于充电线是放电状态,此状态称全电压状态。

(2) TI关断,T2导通:子模块的端口电压等于0,子模块中电容被旁路,子模块电容电压保持稳定,此状态称零电压状态。

(3) TI和T2均关断:此状态称闭锁状态,一般在做障与启动时使用。

图1-4 子模块运行状态及相应电流通路

        闭锁状态发生在两种工况下: ①在模块化多电平换流器启动的初期,换流器运行于不控整流模式,桥臂电流通过二极管 VD1给电容充电: ②当发生非常严重的故障,比如直流侧两极短路时,子模块内的2个IGBT都应被立即关断,并闭锁其门极触发电路,以免因承受过电流而遭到损环。需要说明的是,直流两极短路后IGBT立即闭锁,于是交流系统和故障点间通过桥臂上所有子模块内的二极管VD2构成通路，导致二极管承受较大的短路电流，受器件硅面积限制，二极管只能承受瞬时的冲击电流而不能承担持续性的短路电流。因此，检测到故障时，应立即触发与VD2并联的压接式晶闸管，以便在断路器动作前分担大部分短路电流，保护VD2不受损伤。

2. MMC柔性直流输电建模与仿真

2.1 MMC基本参数选择

2.1.1 桥臂子模块数目的确定

       子模块是构成MMC的最小单元，是MMC拓扑结构中数量最多的元件。MMC输出交流电压的波形质量直接受其电平数的影响，因此研究桥臂子模块的数目是有必要的。在不计桥臂中冗余子模块数目的时候，若MMC直流侧电压为Udc，每一个子模块的电容电压额定值为Uc，则每个桥臂的级联子模块数N应该满足

                                                           (2 -1)

       考虑到实际工程中，在确定MMC桥臂中子模块数目时必须考虑一定的冗余度，以确保柔性直流输电系统的运行可靠性。通常，冗余子模块数目越高，可靠度越高，同时也会增加工程的初期投资。

2.1.2 子模块电容的参数设计

        子模块电容器是子模块中体积最大的元件，其参数的大小直接影响到直流系统的运行特性，此处主要从抑制子模块电容电压稳态波动的角度设计电容值，遵循能量平衡的原则，电容的取值需要满足如下条件：

                        (2-2)

式中：SN——换流器的视在功率；

UN——换流器的视在功率；

ω——工频角频率；

N——峭壁串联子模块数；

UC——每个子模块的电容电压额定值；

ε——电容电压波动率；

M——换流器的调制比；

φ——功率因数角

2.1.3  桥臂电抗器的参数设计

桥臂电抗器是MMC的重要组成部分，太大的电抗器值会增加模块化多电平的换流器不必要的成本，影响控制系统电流跟踪速度，太小则难以满足抑制歇逼的需求。所以，电抗器电感值是一个很重要的问题。对MMC——HVDC的安全稳定运行具有重要的意义。在实际工程中，MMC桥臂电抗器参数设计是要综合各方面的因素进行考虑。桥臂电抗器的参数设计是要从以下四个约束进行考虑：

①满足系统的运行范围；②抑制MMC直流侧故障时桥臂电流上升的速度；③抑制MMC内部的换流；④工程的投资成本。

(1)考虑系统运行范围的电抗器值的选取

由于系统电抗与变压器漏抗为串联关系。交流电流同时流过两者，桥臂电抗与变压器漏抗的取值大小都会影响到交流电流及功率的大小，因此桥臂电抗器值不能够单独设计，需要与变压器漏抗合并等效后计算，等效后的电感为：

                                                                (2-3)  

式中。L为等效电感，其电抗值标幺值为

                                                                                                              (2-4)

根据换流站的运行范围可以得到：

                                                                                    (2-5)

式中，δ为换流器出口电压相对于交流系统电压的移相角。可以由δ的工作范围来确定等效电抗的取值，去掉变压器漏抗，即得到桥臂电抗值。实际工程中一般把δ控制在较小的范围内，当δ的绝对值处于6°~17°时，X*的取值为0.1~0.3。

(2) 抑制MMC直流侧故障时桥臂电流的上升速度的电抗值的选取

在给定暂态电流上升率α（kA/s）的情况下，桥臂电抗器的计算公式如下：

                                                                                                               (2-6)    

(3)抑制MMC内部的换流的电抗值选取

        桥臂电流中不仅包含基波分量，还存在负序性质的二倍频环流。在指定换流大小下，桥臂串联电抗的计算如：

                                                                                (2-7)

 式中，I2f——指定环流的峰值。

2.2 最近电平逼近调制

      最近电平逼近调制（Nearest Level Control，NLC）也称作量化取整法，其原理与数字电路中的A/D变换类似，它的工作机理是从换流器所能生成的电平中选择与调制波采样值最接近的作为控制指令，然后触发相应数目的子模块产生所需的电平输出。

最近电平逼近调制在选择最邻近电平时刻基于公式得到

                                              (2-8)

式中： N(t)——桥臂需要投入的子模块数目；

UCref——子模块电容电压参考值；

uref——桥臂电压参考值。

[  ]——对[  ]内数据四舍五入原则取整。

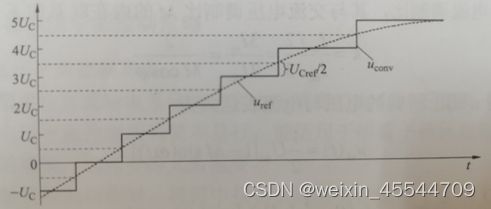
图2-1 最近电平逼近调制原理

      从输出电压波形来看，最近电平逼近调制类似于阶梯波调制，该调制方法原理简单，视线容易，效率高，但是当换流器数目较少时，逼近误差相对较大，地次谐波也随之出现，而在电平数目较高的的应用场合，其原理简单而具有较大的优势。

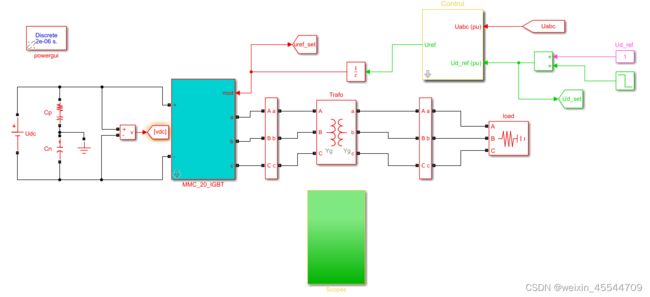
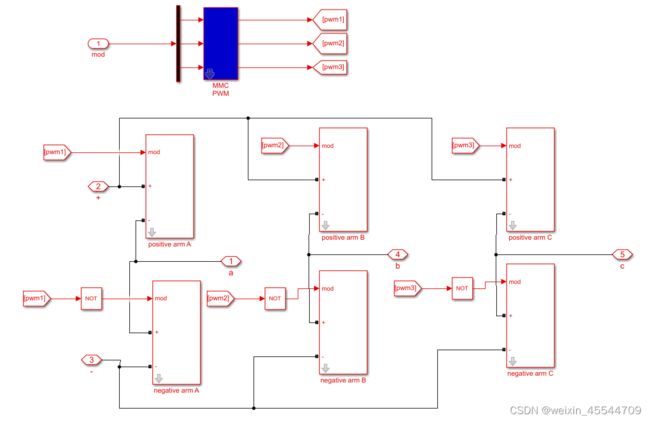
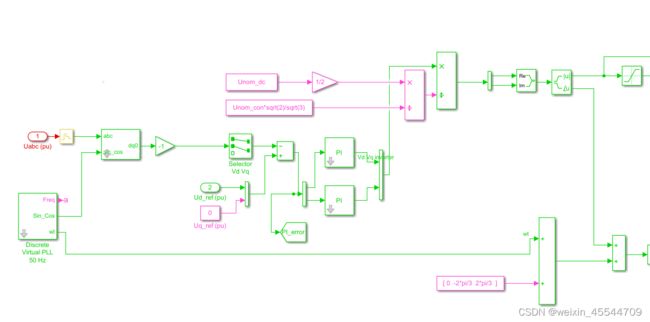
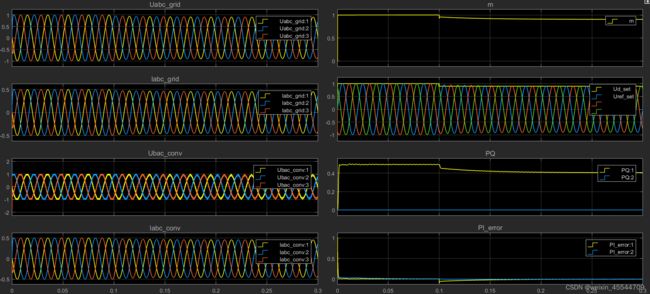
 2.3 仿真模型的建立

本文建立了基于simulink的仿真模型，MMC包含20个子模块，直流电压为1kV，运行稳定

有需要相关指导或者模型的可加QQ：2504024627