Sangria:类似Nova folding scheme的relaxed PLONK for PLONK
1. 引言
前序博客有:
- Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记
- SuperNova:为多指令虚拟机执行提供递归证明
- 基于Nova/SuperNova的zkVM
- Sangria:PLONK + Folding
- 2023年 ZK Hack以及ZK Summit 亮点记
主要见2023年4月 Geometry团队Nicolas Mohnblatt在- Zero Knowledge Summit 9 on April 4 2023 in Lisbon 会议上的分享视频:
- ZK9: Sangria is relaxed PLONK a Nova-like folding scheme for PLONK – Nicolas Mohnblatt (Geometry)
- Nico 2023年3月twitterSNARK recursion survey
微软团队2021年论文 《Nova: Recursive Zero-Knowledge Arguments from Folding Schemes》中首次提出了Folding schemes:
- 将某problem的2个instance 压缩为 同一问题的single instance。如解决了2个数独题,无需展示2个答案,而可以将其合并展示为1个答案。
Folding schemes为实现cheap recursion的关键要素。在Nova论文中仅展示了针对R1CS电路的folding scheme。而Sangria为针对PLONKish电路的folding scheme。
Sangria的开销与Nova的类似:
- Verifier work为常量值,与电路中的行数(即depth)无关
- 引入的常量值开销要比Nova大,但是该代价 带来的好处是 可获得更灵活的arithmetization。
当前Lurk项目在使用Nova方案,详细见Lurk——Recursive zk-SNARKs编程语言。
Sangria也在与相关项目方做相关实现。
2. 为何需要递归,以及现有递归方案
2.1 为何需要递归?——IVC
为何需要递归?
其目的是为了实现 IVC(Incrementally Verifiable Computation)。
对于需要将某函数 F F F执行 n n n次的长计算:
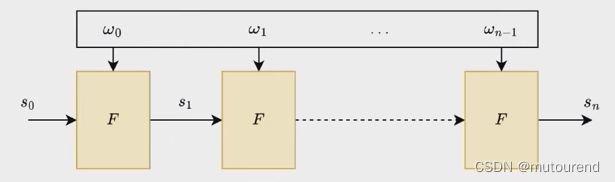
Prover想要证明其知道private inputs w 0 , w 1 , ⋯ , w n − 1 w_0,w_1,\cdots,w_{n-1} w0,w1,⋯,wn−1,使得由初始状态 s 0 s_0 s0执行 n n n次 F F F函数之后, s n s_n sn为正确的最终状态。
实际上,IVC可用于构建:
- zkVMs:可将 F F F函数看成是(如RISC、ARM等)微处理器的一个cycle,对 F F F函数的迭代执行可看成是处理器的运行。
- rollups:将 s s s看成是区块链状态, w w w为incoming交易, F F F为表示区块链状态变化的transition function。rollup可为很多很多区块构建succinct proof。
- VDF(Verifiable Delay Functions):如Open VDF: Accelerating the Nova SNARK-based VDF。
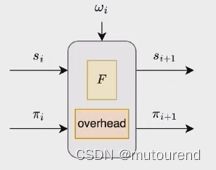
为实现IVC,定义某Prover P F \mathcal{P}_F PF,其输入有某state和某proof,输出为更新的state和更新的proof:
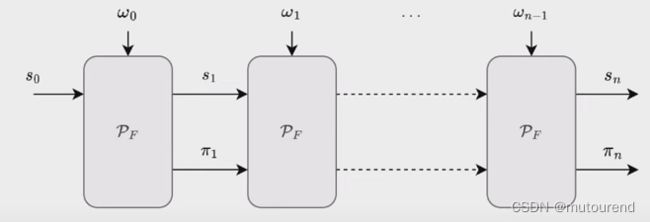
从而可将Prover P F \mathcal{P}_F PF的内部结构拆分为2部分表示:
- 1)函数 F F F:输入某state,执行 F F F函数,输出更新的state。
- 2)overhead:输入某proof,运行overhead,输出更新的proof。overhead主要工作为Verifier验证前一proof,并为 该验证过程的正确执行 生成新的proof。
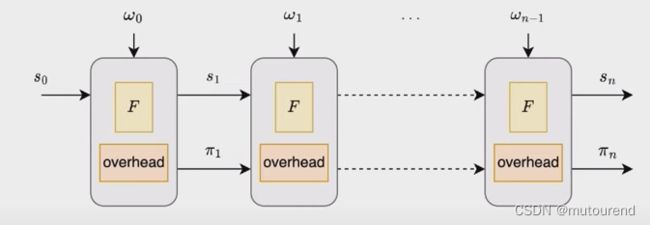
为实现IVC Prover P F \mathcal{P}_F PF: - 需要一些额外的开销来更新proof。这些额外的开销在IVC的每一个step都需要,关键怎么将这些额外的开销做到最低。
2.2 现有IVC方案对比
现有的IVC方案在实现overhead上主要分为:
-
1)SNARK of SNARK:Verifier会读取整个proof,并验证整个proof,无任何延缓操作。【每个step都需要读取完整的proof,并验证完整的proof。】
SNARK of SNARK代表方案有:- Plonky2:为recursive STARK。 2 12 2^{12} 212个gate,不过为wide gate——width of 135 (Goldilocks) elements,且conjectured FRI soundness约为100 bits。
- Fractal:为Groth16 + [BCTV14](2013年论文Succinct Non-Interactive Zero Knowledge for a von Neumann Architecture)。
Fractal很昂贵,有约百万级的R1CS约束。
-
2)Accumulation(atomic)(原子式累加):Verifier会读取整个proof,但只验证部分,会将hard part的验证累加推迟,即递归 n n n次,仅需要对hard part做一次验证。【每个step都需要读取完整的step,并做部分验证,在最后一个step需对hard part进行一次验证即可。】
Accumulation(atomic)(原子式累加)代表方案有: -
3)Accumulation(split)(切分累加):Verifier会读取部分proof,但只验证部分,会将hard part的验证累加推迟,即递归 n n n次,仅需在最后读取一次完整的proof,并对hard part做一次验证。【每个step仅需读取部分proof,并做部分验证,仅需在最后一个step读取一次完整的proof,并执行一次hard part验证。】
Accumulation(split)(切分累加)代表方案有:- [BCLMS21]对应2020年论文Proof-Carrying Data without Succinct Arguments:其牺牲了succinctness。
-
4)Folding:读取unproven instance,将其压缩为a running instance,对proving进行推迟。【每个step读取unproven instance,执行 F F F来获得new running instance,只在最后一个step做证明】
Folding代表方案有:- Nova:比之前方案的overhead开销要便宜很多,仅有约2万个约束。

Sangria关注的点在于,在Nova的基础上,将R1CS电路表示,替换为效率更高的PLONK电路表示。
3. PLONK folding scheme设计思路
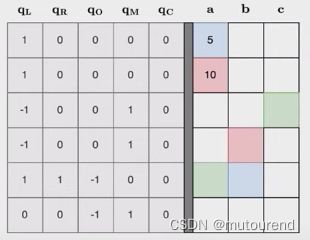
3.1 PLONK Arithmetization定义
-
具有固定size的网格
-
向单元格内填充“数字(有限域)”
-
需遵循一系列rules规则:
-
根据selectors和rules即定义了某circuit。
-
整个trace可分为:
3.2 Folding Scheme定义
folding scheme是将相同电路的2个instance压缩为1个instance,具体定义见ZKMOOC中的下图:
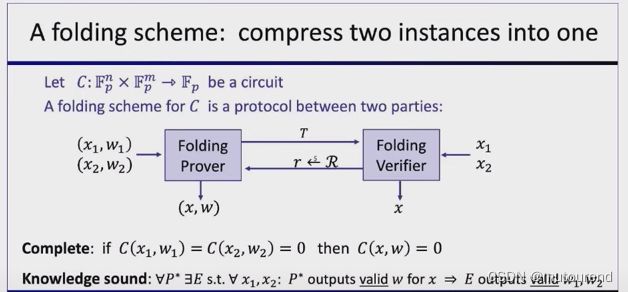
folding schem需满足:
- completeness属性
- knowledge soundness属性
注意Folding scheme不是argument,folding scheme中不证明任何东西,Verifier接收后直接进入下一step——这也是为啥folding scheme更cheaper的理论原因。
3.3 PLONK folding scheme设计方案一
PLONK folding scheme设计方案一:
引入随机值 r r r,random linear combination之后:
- Copy constraints仍然成立。
- gate equation为非线性的,会存在一些问题。
3.4 PLONK folding scheme设计方案二
Nova采用了相应的方案:
- 对gate equation进行relaxed
- Prover对整个trace进行操作,而Verifier操作相应的commitments。commitments值很短,即意味着Verifier仅需做少量工作。
借鉴Nova,PLONK folding scheme设计方案二为——Relaxed PLONK arithmetization:
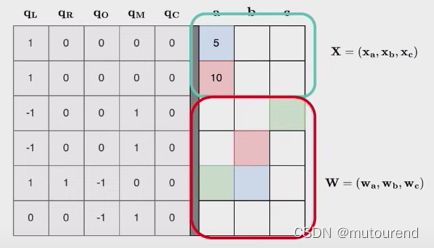
- Witness(私有信息):包括:
- PLONK witness: W = ( w a , w b , w c ) \mathbf{W}=(\mathbf{w}_a,\mathbf{w}_b,\mathbf{w}_c) W=(wa,wb,wc)
- 某error vector: e \mathbf{e} e
- Instance(公开信息):包括:
- public inputs: X = ( x a , x b , x c ) \mathbf{X}=(\mathbf{x}_a,\mathbf{x}_b,\mathbf{x}_c) X=(xa,xb,xc)
- 某scalar值: u u u
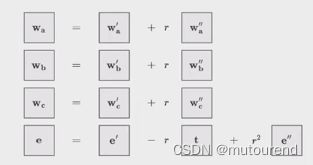
- 以上witness的承诺值:【图片中以方框来表示承诺值】
C o m ( w a ) , C o m ( w b ) , C o m ( w c ) , C o m ( e ) Com(\mathbf{w}_a),Com(\mathbf{w}_b),Com(\mathbf{w}_c), Com(\mathbf{e}) Com(wa),Com(wb),Com(wc),Com(e)
- Relaxed gate equation:【即Sangria的名字来源】
u [ ( q L ) i a i + ( q R ) i b i + ( q O ) i c i ] + ( q M ) i a i b i + u 2 ( q C ) i + e i u[(q_L)_ia_i+(q_R)_ib_i+(q_O)_ic_i]+(q_M)_ia_ib_i+u^2(q_C)_i+e_i u[(qL)iai+(qR)ibi+(qO)ici]+(qM)iaibi+u2(qC)i+ei
这样,上述多项式中除 e i e_i ei之外的各项的degree均为2,从而实现了homogeneous函数。 e i e_i ei作为error项,功能类似可扔的trash,包含了所不想要的内容。
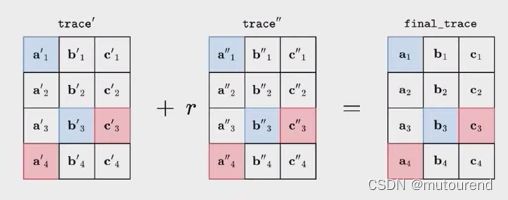
然后仍然引入随机值 r r r,random linear combination之后,folding为:

将folding之后的值插入到relaxed gate equation中,有:
![]()
其中 t \mathbf{t} t为something big and ugly。
根据folding scheme中的completeness属性,若trace正确,则Gate之后值为0,从而有 G a t e ( t r a c e ′ ) = 0 , G a t e ( t r a c e ′ ′ ) = 0 Gate(trace')=0,Gate(trace'')=0 Gate(trace′)=0,Gate(trace′′)=0,剩下的为ugly r t r\mathbf{t} rt。
为摆脱ugly t \mathbf{t} t,可借助上面定义的trash error term e \mathbf{e} e,并将其folding为:
e = e ′ − r t + r 2 e ′ ′ \mathbf{e}=\mathbf{e}'-r\mathbf{t}+r^2\mathbf{e''} e=e′−rt+r2e′′
3.5 PLONK folding scheme设计方案:Sangria
若gate equation为固定的,则 t \mathbf{t} t也是固定的。
因此:
-
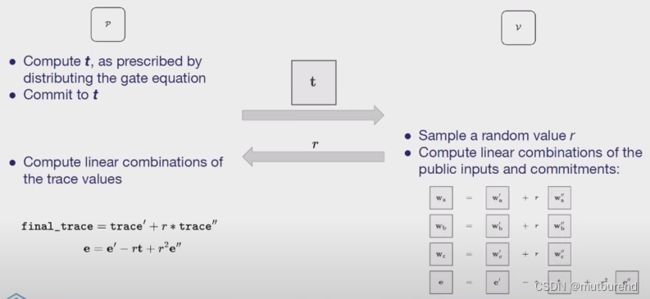
在协议开始之初,Prover可计算 t \mathbf{t} t,并将其承诺值发送给Verifier。
-
Verifier发送随机值 r r r。
-
Prover:
- 计算trace的random linear combination。
Verifier:
- 计算public inputs的random linear combination。
- 计算各witness承诺值的random linear combination。【承诺方案应具有加法同态属性。】
整个交互流程为:【为简化表述,忽略了hiding需求。】
Sangria论文中的各变量的具体值为:【可看出各个变量的值很复杂,ugly。且在论文中考虑了hiding需求。】

4. Sangria性能分析——即overhead开销
Sangria性能分析——即overhead开销,Verifier的主要工作为承诺值的加法运算:【包含5次point addition运算】
实际上,是将 一个standard PLONK instance folding为 一个relaxed PLONK instance:
- standard PLONK instance中没有error项
- Verifier仅需做4次point addition运算。比5次少一次的原因在于:
在实际做IVC时,incoming instance并未relaxed,因此其没有narrow term,所以实际上仅需要4次point addition运算。
因此:
- Sangria overhead的开销为4次point addition运算。
- 而Nova的overhead开销仅为2次point addition运算。Nova方案要更简洁,因为其不需要处理3个witness承诺值,Nova仅需要处理1个witness承诺值。
但Sangria具有更大的灵活性——采用PLONK电路:
- 可添加更多的列
- 可修改gate equation
5. TurboPLONK对Sangria性能的影响
Sangria具有更大的灵活性——采用PLONK电路:
- 1)可添加更多的列(Wider Circuits):
当使用Sangria folding scheme处理wider circuits时,需对每额外增加的列做commit,相应的开销为:【所谓wider circuits,是指具有larger fan-in fan-out at each gate的电路。即gate中多于2个in wire,多于1个out wire的情况。】- 每额外增加一个trace列,Verifier需额外多做一次point addition运算。
- 2)可修改gate equation(Custom Gates):
当使用Sangria folding scheme处理custom Gates(higher degree Gates)时:- degree为 d d d的gate,将relaxed with powers of u u u up to u d u^d ud。
- error的folding equation形如:
e = e ′ − r t 1 − r 2 t 2 − ⋯ − r d − 1 t d − 1 + r d e ′ ′ \mathbf{e}=\mathbf{e}'-r\mathbf{t}_1-r^2\mathbf{t}_2-\cdots - r^{d-1}\mathbf{t}_{d-1}+r^d\mathbf{e''} e=e′−rt1−r2t2−⋯−rd−1td−1+rde′′ - 相应的开销为:
- degree每额外加1:Prover的message中需额外包含一个新的承诺值,Veriifer需额外多做一次point addition运算。
6. 设计空间——递归开销的最小值
设计递归证明方案的关键在于:
- 如何让overhead开销最小化
当前,Nova电路有约2万个约束,其中1.2万个为point addition。
开放问题为:
- 对本文第5章的场景,采用wider circuits和custom gates的优势,能否超过给folding Verifier引入额外point additions运算开销的劣势?即如何在递归overhead开销 与 电路灵活性 之间权衡?
7. 后续工作
后续安排有:
- Sangria为对标Nova的PLONK folding scheme,未来可能有对标SuperNova的PLONK folding scheme。
- 当前正在做standard PLONK的Sangria代码实现。
- 针对ultraPLONK,lookup-enabled traces的folding scheme。
- 可能的非凡电路表示:具有cheaper overhead和super cheap IVC。