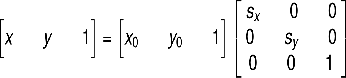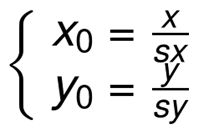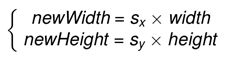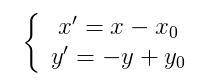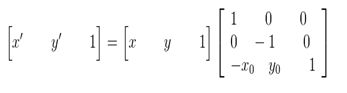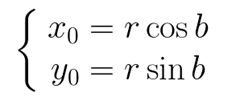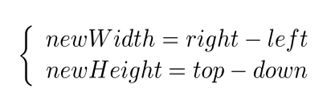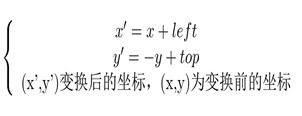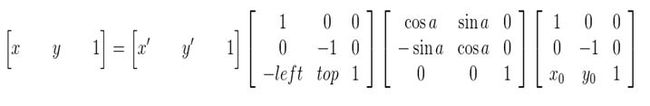OpenCV2:图像的几何变换,平移、镜像、缩放、旋转(2)
在OpenCV2:图像的几何变换,平移、镜像、缩放、旋转(1)主要介绍了图像变换中的向前映射、向后映射、处理变换过程中浮点坐标像素值的插值算法,并且基于OpenCV2实现了两个简单的几何变换:平移和镜像变换。本文主要稍微复杂点的两个几何变换:缩放和旋转。
1.图像缩放
图像的缩放主要用于改变图像的大小,缩放后图像的图像的宽度和高度会发生变化。水平缩放系数,控制图像宽度的缩放,其值为1,则图像的宽度不变;垂直缩放系数控制图像高度的缩放,其值为1,则图像的高度不变。如果水平缩放系数和垂直缩放系数不相等,那么缩放后图像的宽度和高度的比例会发生变化,会使图像变形。要保持图像宽度和高度的比例不发生变化,就需要水平缩放系数和垂直缩放系数相等。
左边的图像水平缩放系数和垂直缩放系数都是0.5;右边的图像的水平缩放系数为1,垂直缩放系数为0.5,缩放后图像宽度和高度比例发生变化,图像变形。
1.1 缩放原理
设水平缩放系数为sx,垂直缩放系数为sy,(x0,y0)为缩放前坐标,(x,y)为缩放后坐标,其缩放的坐标映射关系: ![]()
矩阵表示的形式为:
这是向前映射,在缩放的过程改变了图像的大小,使用向前映射会出现映射重叠和映射不完全的问题,所以这里更关心的是向后映射,也就是输出图像通过向后映射关系找到其在原图像中对应的像素。
向后映射关系:
1.2基于OpenCV的缩放实现
在图像缩放的时首先需要计算缩放后图像的大小,设newWidth,newHeight为缩放后的图像的宽和高,width,height为原图像的宽度和高度,那么有:
然后遍历缩放后的图像,根据向后映射关系计算出缩放的像素在原图像中像素的位置,如果得到的浮点坐标,就需要使用插值算法取得近似的像素值。
根据上面公式可知,缩放后图像的宽和高用原图像宽和高和缩放因子相乘即可。
int rows = static_cast<int>(src.rows * xRatio + 0.5); int cols = static_cast<int>(src.cols * yRatio + 0.5);
在向后映射时有可能得到浮点坐标,这里使用最邻近插值和双线性插值来处理。
最邻近插值
for (int i = 0; i < rows; i++){ int row = static_cast<int>(i / xRatio + 0.5); if (row >= src.rows) row--; origin = src.ptr<uchar>(row); p = dst.ptr<uchar>(i); for (int j = 0; j < cols; j++){ int col = static_cast<int>(j / yRatio + 0.5); if (col >= src.cols) col--; p[j] = origin[col]; } }
最邻近插值只需要对浮点坐标“四舍五入”运算。但是在四舍五入的时候有可能使得到的结果超过原图像的边界(只会比边界大1),所以要进行下修正。
双线性插值
双线性插值的精度要比最邻近插值好很多,相对的其计算量也要大的多。双线性插值使用浮点坐标周围四个像素的值按照一定的比例混合近似得到浮点坐标的像素值。
设浮点坐标F,其周围的四个整数坐标别为T1,T2,T3,T4,并且F和其左上角的整数坐标的纵轴差的绝对值为n,横轴差的绝对值为n。据上一篇文章分析可得浮点坐标F的像素值T,有下面公式计算得到:
F1为([F.y],F.x),F2为([F.y]+1,F.x)。具体的参见OpenCV2:图像的几何变换,平移、镜像、缩放、旋转(1).
在实现的时候首先要根据浮点坐标计算出其周围的四个整数坐标
double row = i / xRatio; double col = j / yRatio; int lRow = static_cast<int>(row); int nRow = lRow + 1; int lCol = static_cast<int>(col); int rCol = lCol + 1; double u = row - lRow; double v = col - lCol;
缩放放后图像的坐标(i,j),根绝向后映射关系找到其在原图像中对应的坐标(i / xRatio,j / yRatio),接着找到改坐标周围的四个整数坐标(lcol,lRow),(lCol,nrow),
(rCol,lRow),(rCo1,nRow)。下面根据双线性插值公式得到浮点坐标的像素值
//坐标在图像的右下角 if ((row >= src.rows - 1) && (col >= src.cols - 1)) { lastRow = src.ptr<Vec3b>(lRow); p[j] = lastRow[lCol]; } //最后一行 else if (row >= src.rows - 1) { lastRow = src.ptr<Vec3b>(lRow); p[j] = v * lastRow[lCol] + (1 - v) * lastRow[rCol]; } //最后一列 else if (col >= src.cols - 1){ lastRow = src.ptr<Vec3b>(lRow); nextRow = src.ptr<Vec3b>(nRow); p[j] = u * lastRow[lCol] + (1 - u) * nextRow[lCol]; } else { lastRow = src.ptr<Vec3b>(lRow); nextRow = src.ptr<Vec3b>(nRow); Vec3b f1 = v * lastRow[lCol] + (1 - v) * lastRow[rCol]; Vec3b f2 = v * nextRow[lCol] + (1 - v) * lastRow[rCol]; p[j] = u * f1 + (1 - u) * f2; }
由于使用四个像素进行计算,在边界的时候,会有不存在的像素,这里把在图像的右下角、最后一行、最后一列三种特殊情形分别处理。
2.图像旋转
2.1旋转原理
图像的旋转就是让图像按照某一点旋转指定的角度。图像旋转后不会变形,但是其垂直对称抽和水平对称轴都会发生改变,旋转后图像的坐标和原图像坐标之间的关系已不能通过简单的加减乘法得到,而需要通过一系列的复杂运算。而且图像在旋转后其宽度和高度都会发生变化,其坐标原点会发生变化。
图像所用的坐标系不是常用的笛卡尔,其左上角是其坐标原点,X轴沿着水平方向向右,Y轴沿着竖直方向向下。而在旋转的过程一般使用旋转中心为坐标原点的笛卡尔坐标系,所以图像旋转的第一步就是坐标系的变换。设旋转中心为(x0,y0),(x’,y’)是旋转后的坐标,(x,y)是旋转后的坐标,则坐标变换如下:
矩阵表示为:
在最终的实现中,常用到的是有缩放后的图像通过映射关系找到其坐标在原图像中的相应位置,这就需要上述映射的逆变换
坐标系变换到以旋转中心为原点后,接下来就要对图像的坐标进行变换。
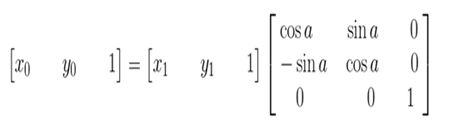
上图所示,将坐标(x0,y0)顺时针方向旋转a,得到(x1,y1)。
旋转前有:
旋转a后有:
矩阵的表示形式:
其逆变换:
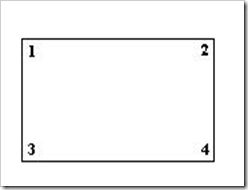
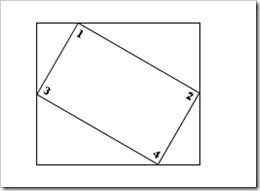
由于在旋转的时候是以旋转中心为坐标原点的,旋转结束后还需要将坐标原点移到图像左上角,也就是还要进行一次变换。这里需要注意的是,旋转中心的坐标(x0,y0)实在以原图像的左上角为坐标原点的坐标系中得到,而在旋转后由于图像的宽和高发生了变化,也就导致了旋转后图像的坐标原点和旋转前的发生了变换。
上边两图,可以清晰的看到,旋转前后图像的左上角,也就是坐标原点发生了变换。
在求图像旋转后左上角的坐标前,先来看看旋转后图像的宽和高。从上图可以看出,旋转后图像的宽和高与原图像的四个角旋转后的位置有关。
设top为旋转后最高点的纵坐标,down为旋转后最低点的纵坐标,left为旋转后最左边点的横坐标,right为旋转后最右边点的横坐标。
旋转后的宽和高为newWidth,newHeight,则可得到下面的关系:
也就很容易的得出旋转后图像左上角坐标(left,top)(以旋转中心为原点的坐标系)
故在旋转完成后要将坐标系转换为以图像的左上角为坐标原点,可由下面变换关系得到:
矩阵表示:
其逆变换:
综合以上,也就是说原图像的像素坐标要经过三次的坐标变换:
- 将坐标原点由图像的左上角变换到旋转中心
- 以旋转中心为原点,图像旋转角度a
- 旋转结束后,将坐标原点变换到旋转后图像的左上角
可以得到下面的旋转公式:(x’,y’)旋转后的坐标,(x,y)原坐标,(x0,y0)旋转中心,a旋转的角度(顺时针)
这种由输入图像通过映射得到输出图像的坐标,是向前映射。常用的向后映射是其逆运算
2.2基于OpenCV的实现
得到了上述的旋转公式,实现起来就不是很困难了.
首先计算四个角的旋转后坐标(以旋转中心为坐标原点)
const double cosAngle = cos(angle); const double sinAngle = sin(angle); //原图像四个角的坐标变为以旋转中心的坐标系 Point2d leftTop(-center.x, center.y); //(0,0) Point2d rightTop(src.cols - center.x,center.y); // (width,0) Point2d leftBottom(-center.x, -src.rows + center.y); //(0,height) Point2d rightBottom(src.cols - center.x, -src.rows + center.y); // (width,height) //以center为中心旋转后四个角的坐标 Point2d transLeftTop, transRightTop, transLeftBottom, transRightBottom; transLeftTop = coordinates(leftTop, angle); transRightTop = coordinates(rightTop, angle); transLeftBottom = coordinates(leftBottom, angle); transRightBottom = coordinates(rightBottom, angle);
需要注意的是要将原图像四个角的坐标变为以旋转中心为坐标原点的坐标系坐标。然后通过旋转变换公式
由于旋转角度的不同旋转后四个角的位置和其在原图像的位置是不相同的,也就是说原图像的左上角在旋转后不一定是旋转后图像的左上角,有可能是右下角。所以在计算旋转后图像的宽度就不能使用原图右上角旋转后的横坐标减去原图像左下角旋转后的横坐标,高度也是如此。(在查找资料时发现,大部分都是使用这种方式计算的图像的宽度和高度)。
//计算旋转后图像的width,height double left = min({ transLeftTop.x, transRightTop.x, transLeftBottom.x, transRightBottom.x }); double right = max({ transLeftTop.x, transRightTop.x, transLeftBottom.x, transRightBottom.x }); double top = max({ transLeftTop.y, transRightTop.y, transLeftBottom.y, transRightBottom.y }); double down = min({ transLeftTop.y, transRightTop.y, transLeftBottom.y, transRightBottom.y }); int width = static_cast<int>(abs(left - right) + 0.5); int height = static_cast<int>(abs(top - down) + 0.5);
计算旋转图像的宽度,可以使用四个角旋转后最右边点的横坐标减去最左边点的横坐标;高度时最上边点的纵坐标减去最下边点的纵坐标。
然后,就可以使用最终的那个旋转公式,处理图像的每一个像素了。
const double num1 = -abs(left) * cosAngle - abs(top) * sinAngle + center.x; const double num2 = abs(left) * sinAngle - abs(top) * cosAngle + center.y; Vec3b *p; for (int i = 0; i < height; i++) { p = dst.ptr<Vec3b>(i); for (int j = 0; j < width; j++) { //坐标变换 int x = static_cast<int>(j * cosAngle + i * sinAngle + num1 + 0.5 ); int y = static_cast<int>(-j * sinAngle + i * cosAngle + num2 + 0.5 ); if (x >= 0 && y >= 0 && x < src.cols && y < src.rows) p[j] = src.ptr<Vec3b>(y)[x]; } }
这使用的插值方法是最邻近插值,双线性插值的实现方法和图像缩放类似,不再赘述。
使用上述算法进行图像旋转,会发现不论使用图像内的那个位置作为旋转的中心,最后得到的结果都是一样的。这是因为,不同位置作为旋转中心,旋转后图像的大小都是一样,所不同的只是其位置。而在最后的一次变换中(图像旋转用了三次坐标变换),统一的把坐标原点移到了旋转后图像的左上角。这就相当于对图像做了一次平移,把其位置也挪到了一起,最后旋转得到的图像也就一样了。
如果,在旋转结束后把坐标原点不是移到旋转后图像的左上角,而是原图像的左上角,会是怎么一个情形呢?
就像上图,图像的部分区域会被截掉。当然,这时旋转中心不同的话最终得到的图像也就不同了,被截掉的部分不相同。
3.组合变换
组合变换就是把多种几何放在一起进行。上面推导了旋转的变换公式,那么组合变换也就不是很困难了,无非是多了几个矩阵相乘。比较常见的组合变换:缩放+旋转+平移,下面以此为例推导下组合变换的公式。
- 缩放
设(x0,y0)是缩放后的坐标,(x,y)是缩放前的坐标,sx,sy为缩放因子
- 平移
设(x0,y0)是平移后的坐标,(x,y)是平移前的坐标,dx,dy为偏移量
- 旋转
设(x0,y0)是旋转后坐标,(x,y)是旋转前坐标,(m,n)是旋转中心,a是旋转的角度,(left,top)是旋转后图像的左上角坐标
分别得到了三个变换矩阵,按照缩放、平移、旋转的顺序组合起来
组合变换的时候要注意顺序,毕竟矩阵的左乘和右乘是不一样的。
4.最后
到现在,写的最长的一篇文章。和上一篇放到一起弄了差不多快一个周了,算法的实现除了旋转有个几次挫折外,其余的几种变换都很顺利。耗时间的主要是画图和数学公式,画图一直没有找到合适的工具,不了了之;数学公式特意花了一天的时间学了Latex,并且找了些把Tex转换为HTML的工具,但是效果都不是很好,还是粘贴图片。没有图,有些东西只靠文字确实很难说的清楚,抽空得学习学习MATLAB画图了。