Directed Minimum Spanning Tree: Chu-Liu/Edmonds Algorithm

我们的现代数据库大作业要求实现一个图查询系统，包括基于属性的子图查询、可达性查询（可选）、最短路径查询（可选）、TopK最短路径查询（可选）、图形化展示（可选）等功能。分成子图同构查询小组以及可达性及TopK路径查询小组。

小组长之前研究了Efficiently answering reachability queries on very large directed graphs这篇论文，关于Path-tree计算可达性的，其中需要构造最大生成树(无需固定root)，于是负责打酱油的我就开始琢磨单连通有向图的最大生成树算法Edmonds Algorithm了。

 

 

Edmonds Algorithm介绍

---

Solving The Directed MST Problem

Chu and Liu [2], Edmonds [3], and Bock [4] have independently given efficient algorithms for finding the MST on a directed graph. The Chu-Liu and Edmonds algorithms are virtually identical; the Bock algorithm is similar but stated on matrices instead of on graphs. Furthermore, a distributed algorithm is given by Humblet [5]. In the sequel, we shall briefly illustrate the Chu-Liu/Edmonds algorithm, following by a comprehensive example (due to [1]). Reader can also refer to [6] [7] for an efficient implementation, O(mlogn) and O(n^2) for dense graph, of this algorithm.

Chu-Liu/Edmonds Algorithm

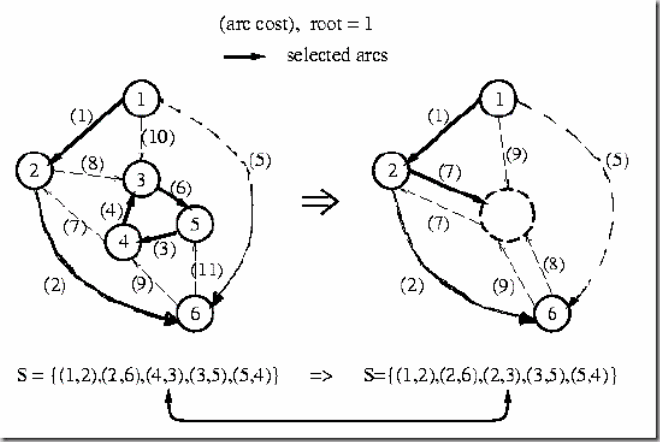
1. Discard the arcs entering the root if any; For each node other than the root, select the entering arc with the smallest cost; Let the selected n-1 arcs be the set S.
2. If no cycle formed, G(N,S) is a MST. Otherwise, continue.
3. For each cycle formed, contract the nodes in the cycle into a pseudo-node (k), and modify the cost of each arc which enters a node (j) in the cycle from some node (i)outside the cycle according to the following equation.

   c(i,k)=c(i,j) - (c(x(j),j) - min_{j}(c(x(j),j))

   where c(x(j),j) is the cost of the arc in the cycle which enters j.

4. For each pseudo-node, select the entering arc which has the smallest modified cost; Replace the arc which enters the same real node in Sby the new selected arc.
5. Go to step 2 with the contracted graph.

The key idea of the algorithm is to find the replacing arc(s) which has the minimum extra cost to eliminate cycle(s) if any. The given equation exhibits the associated extra cost. The following example illustrates that the contraction technique finds the minimum extra cost replacing arc (2,3) for arc (4,3) and hence the cycle is eliminated.

 

References

1. E. Lawler, ``Combinatorial optimization: networks and matroids'', Saunders College Publishing, 1976.
2. Y. J. Chu and T. H. Liu, ``On the shortest arborescence of a directed graph'', Science Sinica, v.14, 1965, pp.1396-1400.
3. J. Edmonds, ``Optimum branchings'', J. Research of the National Bureau of Standards, 71B, 1967, pp.233-240.
4. F. Bock, ``An algorithm to construct a minimum spanning tree in a directed network'', Developments in Operations Research, Gordon and Breach, NY, 1971, pp. 29-44.
5. P. Humblet, ``A distributed algorithm for minimum weighted directed spanning trees'', IEEE Trans. on Communications, v.COM-31, n.6, 1983, pp.756-762.
6. R. E. Tarjan, ``Finding Optimum Branchings'', Networks, v.7, 1977, pp.25-35.
7. P.M. Camerini, L. Fratta, and F. Maffioli, ``A note on finding optimum branchings'', Networks, v.9, 1979, pp.309-312.

 

下面是Wiki上的一段算法描述，包括了计算最后最大生成树总权值的计算。

BV: a vertex bucket

BE: an edge bucket

G₀ = (V₀,E₀) ：the original digraph.

v : a vertex

e ：an edge of maximum positive weight that is incident to v

C_i : a circuit

u_i is a replacement vertex for C_i

 

算法复杂度的改进

---

其中，关于算法复杂度Wiki上是这样描述的：

The order of this algorithm is . There is a faster implementation of the algorithm by Robert Tarjan. The order is for a sparse graph and for a dense graph. This is as fast as Prim's algorithm for an undirected minimum spanning tree. In 1986, Gabow, Galil, Spencer, and Tarjan made a faster implementation, and its order is .

Fibonacci 堆是Fredman 和Tarjan 于1984 年发明的，这个Tarjan将F-Heaps应用到很多图算法中，减少了算法复杂度，比如说86年用于Edmonds Algorithm的这篇paper：

H. N. Gabow, Z. Galil, T. Spencer, and R. E. Tarjan, “Efficient algorithms for finding minimum spanning trees in undirected and directed graphs,” Combinatorica 6 (1986), 109-122.

By observing that in certain situations items can be moved among F-heaps
in  O(1)  amortized time per item moved, we obtain an implementation  of Edmonds' minimum directed spanning tree algorithm [16] with a running time of O (n log n +m)

…

[16] R.  E. TARJAN, Applications of path  compression on balanced trees,  J.  Assoc.  Comput.  Mach. 26  (1979), 690--715.

 

Tarjan版本的实现

---

Wiki最后给了两个实现的链接

Edmonds's algorithm ( edmonds-alg ) – An open source implementation of Edmonds's algorithm written in C++ and licensed under the MIT License. This source is using Tarjan's implementation for the dense graph.

The package edmonds-alg contains a C++-implementation of Edmonds's optimum branching algorithm as described by Tarjan in 1977.

 

AlgoWiki – Edmonds's algorithm - A public-domain implementation of Edmonds's algorithm written in Java.

反正整合到我的代码里之后，我是无法理解代码的行为，看到有人说这个AlgoWiki的实现中getCycles()有问题，并且提供了一份Tarjan版本的新的实现，不知道这个好不好使。

Tarjan的论文：Finding Optimum Branchings  

上述论文的修正: A Note on Finding Optimum Branchings

 

Coolshell上介绍过一些有意思的算法代码，有Edmonds’s Matching Algorithm的Java实现，细看发现这个不是求最大生成树的Edmonds‘s Algorithm算法，白高兴了。

 

补充一个matlab的:

http://www.mathworks.com/matlabcentral/fileexchange/24327-maximumminimum-weight-spanning-tree-directed

http://www.mathworks.com/matlabcentral/fileexchange/24899

 

固定root的算法：

1. 删去所有自己连向自己的入边。
2. 移除树根的全部入边。
3. 判断树根能不能连到图上各个点，否则生成树不存在。
4. 重复以下步骤，直到形成生成树为止：
4.1 找出图上每个点的最小入边。O(E)
4.2 找出所有水母(环)。如果没有水母就表示目前已是最小生成树。O(V)
4.3 调整所有进入水母环的边的权重。O(E)
w(a, x) -= w(å, x)，åx是x点的最小入边，ax为其他连入x点的边。
4.4 收缩水母环成为一点。O(E)

不固定root的算法

1. 删去所有自己连向自己的入边。
2. 重复以下步骤，直到形成生成树为止：
2.1 找出图上每个点的最小入边。O(E)
如果有两个点以上找不到入边，则表示生成树不存在。
（找不到入边的点可作为生成树树根）
2.2 找出所有水母。如果没有水母就表示目前已是最小生成树。O(V)
2.3 调整所有进入水母环的边的权重。O(E)
w(a, x) -= w(å, x)，åx是x点的最小入边，ax为其他连入x点的边。
2.4 收缩水母环成为一点。O(E)

于是我开始使用两年没摸过的Java了。。。先把比较弱的AlgoWiki整合到小组代码框架里，再捣鼓下用F-heap优化算法的Tarjan's implementation的C++实现，，改成Java版本的。

 

AlgoWiki的算法伪码，固定root版本，得改改

Algorithm Overview

• Remove all edges going into the root node (2)
• For each node, select only the incoming edge with smallest weight (4.1)
• For each circuit that is formed: (4.2)
  • edge "m" is the edge in this circuit with minimum weight
  • Combine all the circuit's nodes into one pseudo-node "k"  (4.4)
  • For each edge "e" entering a node in "k" in the original graph: (4.3) 
    • edge "n" is the edge currently entering this node in the circuit
    • track the minimum modified edge weight between each "e" based on the following:
      • modWeight = weight("e") - ( weight("n") - weight("m") )
  • On edge "e" with minimum modified weight, add edge "e" and remove edge "n"

有C++基础，阅读Java代码，加之谷歌娘，还是比较无障碍的

【Java】Final 与 C++ Const的区别

Comparator和Comparable在排序中的应用

基于红黑树的TreeMap类使用实例解析

 

英文

The Directed Minimum Spanning Tree Problem Description of the algorithm summarized(总结) by Shanchieh Jay Yang, May 2000.

http://en.wikipedia.org/wiki/Edmonds'_algorithm

http://en.vionto.com/show/me/Edmonds's+algorithm

中文

http://hi.baidu.com/zhanggmcn/item/aed6f75d0247e710aaf6d7e7

http://acm.nudt.edu.cn/~twcourse/Tree.html#a17