基础算法-子矩阵的和
1 课堂笔记
2 详解
二维前缀和推导
如图:
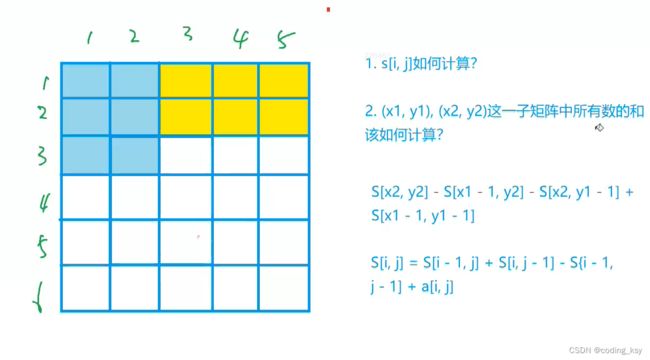
紫色面积是指(1,1)左上角到(i,j-1)右下角的矩形面积, 绿色面积是指(1,1)左上角到(i-1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。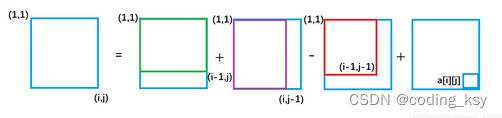
从图中我们很容易看出,整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] - 重复加的红色的面积s[i-1][j-1]+小方块的面积a[i][j];
因此得出二维前缀和预处理公式
s[i] [j] = s[i-1][j] + s[i][j-1 ] + a[i] [j] - s[i-1][ j-1]
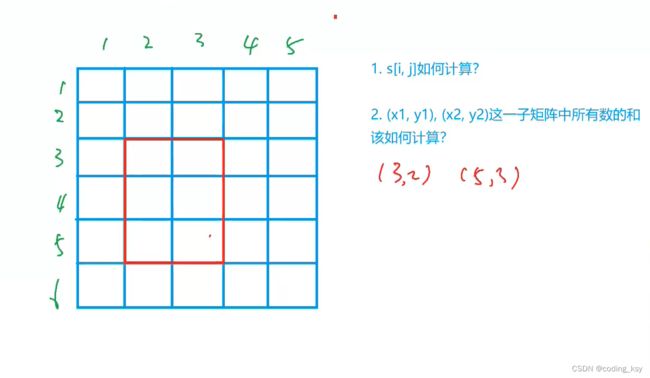
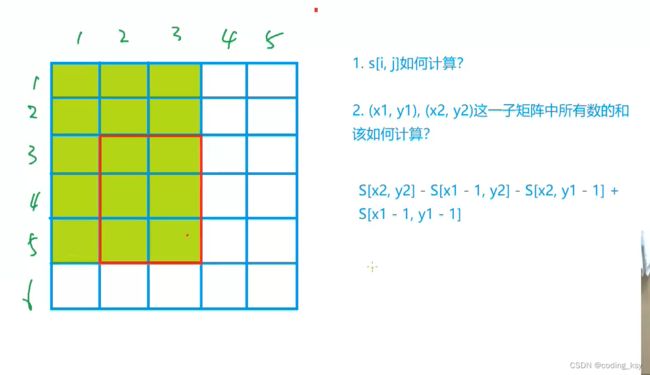
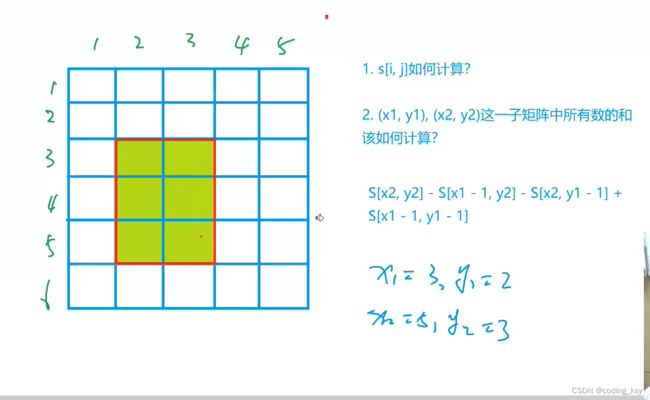
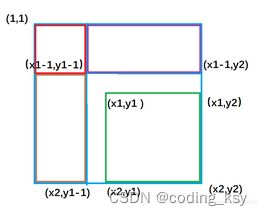
接下来回归问题去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。
紫色面积是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面积 ,黄色面积是指(1,1)左上角到(x2,y1-1)右下角的矩形面积;
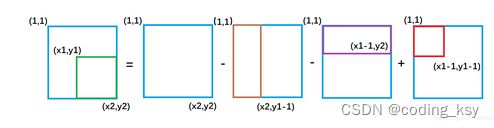
绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]
因此二维前缀和的结论为:
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
总结:
20201217174751639.png
前缀和与差分的个人心得总结
代码:
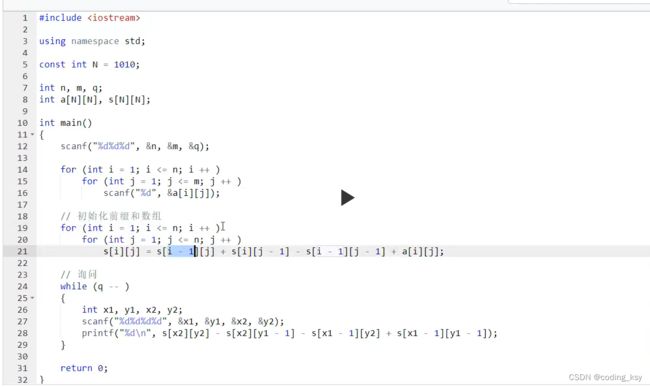
#include
using namespace std;
const int N = 1010;
int n, m, q;
int s[N][N];
int main()
{
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &s[i][j]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
while (q -- )
{
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
}
return 0;
}
2 代码
3.代码解析
#include
using namespace std;
const int maxn=1010;
int a[maxn][maxn],s[maxn][maxn];
int n,m,q,x1,y1,x2,y2;
int main(){
scanf("%d%d%d",&n,&m,&q);
//为数组赋值
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
}
}
//为前缀和赋值
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
s[i][j] = s[i][j-1] + s[i-1][j] - s[i-1][j-1] +a[i][j];
}
}
//输出结果
while(q--){
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
}
} 参考文献
作者:林小鹿
链接:https://www.acwing.com/solution/content/27301/
来源:AcWing