深度学习与神经网络

引言

深度学习的名字来源于其使用的神经网络有很多层，也就是“深”层网络。这些深层网络可以学习并表示数据的高级别抽象，从而捕捉输入数据中的复杂模式。每一层的神经元都根据前一层的输出进行学习，这样，每一层都可以根据前一层的特征表示学习更高级别的特征表示。

举个例子，如果我们用深度学习模型来处理图像，模型的前几层可能会学习到诸如边缘、颜色和纹理等低级特征，然后中间的几层可能会学习到诸如部分物体形状和特定物体部分等中级特征，最后的几层可能会学习到整个物体的表示。

深度学习的一个核心理念就是通过增加网络的深度和宽度来提升模型的表现力，同时，使用反向传播（Backpropagation）和梯度下降（Gradient Descent）等优化算法，不断调整神经网络的参数，使得模型的预测结果与实际结果的差距（也就是损失函数的值）最小。

深度学习的进步对许多领域都产生了巨大影响，例如计算机视觉、自然语言处理、音频处理和强化学习等。然而，深度学习也有其局限性，例如对大量标注数据的依赖，模型的可解释性差，以及训练需要大量计算资源等问题。本文主要讨论深度学习的一些基础性知识

Playground地址： http://playground.tensorflow.org/

1. 神经网络

1.1 什么是神经网络

神经网络是一种模拟人脑神经元行为的计算模型，神经网络由大量的神经元（在计算领域中常被称为“节点”或“单元”）组成，并且这些神经元被分为不同的层，分别为输入层、隐藏层和输出层。每一个神经元都与前一层的所有神经元相连接，连接的强度（或权重）代表了该连接的重要性。神经元接收前一层神经元的信息（这些信息经过权重加权），然后通过激活函数（如Sigmoid、ReLU等）处理，将结果传递到下一层。

输入层接收原始数据，隐藏层负责处理这些数据，而输出层则将处理后的结果输出。对于深度神经网络来说，存在多个隐藏层，这使得网络能够学习并表示更复杂的特征和函数。
神经网络的训练通常依赖于一种名为“反向传播”（backpropagation）的算法。这个算法先将输入数据（如图片、文本等）通过网络前向传播得到预测结果，然后计算预测结果与真实结果之间的误差（即损失函数的值），最后将这个误差反向传播回网络，按照梯度下降的策略更新各层的权重，以期减少预测误差。

1.2 神经元

神经元是组成神经网络的最基本单位，它起初来源于人体，模仿人体的神经元，功能也与人体的神 经元一致，得到信号的输入，经过数据处理，然后给出一个结果作为输出或者作为下一个神经元的输入。

• 输入：是特征向量。特征向量代表的是变化的方向。或者说，是最能代表这个事物的特征的方向
• 权重（权值）：就是特征值。有正有负，加强或抑制，同特征值一样。权重的绝对值大小，代表了输入信号对神经元的影响的大小。
  

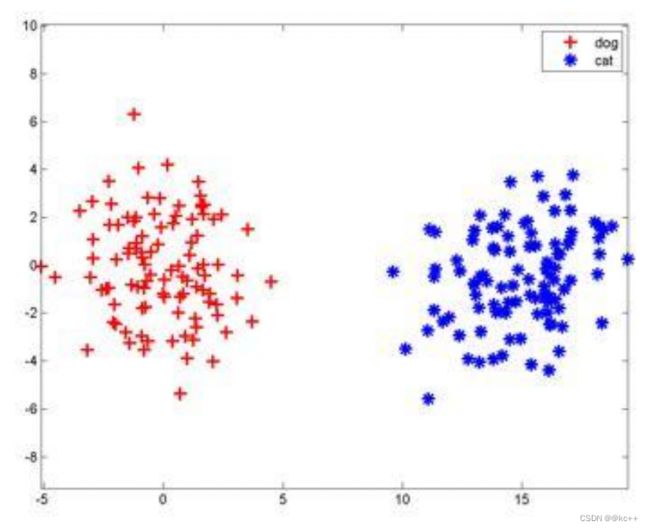
最简单的把这两组特征向量分开的方法？
ax_+by+c=0 ->y = kx+b ->y=wx+b
把上式推广到n维空间：
h = a1x1+a2x2+…+anxn+a0 = 0
神经元就是当h大于0时输出1，h小于0时输出0这么一 个模型，它的实质就是把特征空间一切两半，认为两半分别属于两个类。那么此时神经元只能实现“一刀切”的效果，要解决这个问题，就可以进行构建多层神经网络。

1.3 多层神经网络

多层神经网络，也被称为深度神经网络或多层感知器（MLP, Multilayer Perceptron），它是一种由多个神经元（或称为节点）层组成的网络。这些层包括一个输入层，一个或多个隐藏层和一个输出层。

1. 输入层：这是网络的最底层，它直接接收输入数据。例如，如果我们正在处理图像数据，那么输入层的每个神经元可能会接收图像的一个像素值。在输入层，我们不对数据进行任何处理，只是简单地传递给下一层。
2. 隐藏层：这些是在输入层和输出层之间的层，被称为"隐藏"，是因为我们在训练过程中无法直接观察到这些层的状态。每个隐藏层的神经元将从前一层接收输入，然后通过激活函数（如Sigmoid、ReLU等）对输入进行非线性转换，并将结果传递给下一层。这些隐藏层可以帮助神经网络学习更复杂的特征和模式。
3. 输出层：这是网络的最顶层，负责输出网络的最终预测结果。输出层的神经元数量通常取决于具体的任务需求。例如，对于多类分类问题，输出层的神经元数量可能等于类别的数量。

当网络有很多隐藏层时，我们通常称其为深度神经网络。随着深度的增加，网络能够学习和表示更复杂的模式和特征。

2. 激活函数

2.1 什么是激活函数

在神经网络中，激活函数是用于将神经元的输入信号转化为输出信号的函数。它的主要作用是向网络引入非线性特性，因为如果没有激活函数，不论神经网络有多少层，它最终都能被一个线性模型所表示，那样的话就无法表示复杂的模式和函数。

常用的一些激活函数（满足 1 非线性 2 可微性 3 单调性）

2.2 激活函数的作用

1. 引入非线性：如果我们没有在神经网络中使用激活函数，那么无论我们堆叠多少层的网络，最终得到的仍然只是输入的线性变换。而实际上，我们希望神经网络能够处理更为复杂的、非线性的问题，例如图片分类、语音识别等。通过使用非线性的激活函数，神经网络可以学习并表示更复杂的模式。
2. 决定神经元是否激活：激活函数可以帮助我们决定一个神经元是否应该被激活，即这个神经元是否应该对输入信息做出反应。例如，如果我们使用ReLU激活函数，那么当神经元的输入小于0时，神经元的输出就会是0，我们可以认为这个神经元没有被激活；当输入大于0时，输出就是输入本身，我们可以认为这个神经元被激活了。
3. 压缩神经元的输出范围：某些类型的激活函数（如sigmoid和tanh）可以将神经元的输出压缩到一个固定的范围内（如0到1或-1到1），这对于某些类型的任务（如分类任务，需要输出类别的概率）非常有用。
4. 帮助反向传播：在神经网络的训练过程中，我们使用一种叫做反向传播的技术来调整神经网络的参数，而激活函数的选择会影响反向传播过程中梯度的计算。

2.3 常用激活函数解析

sigmoid函数
这是最早被广泛使用的激活函数之一，函数形式为 f(x) = 1 / (1 + exp(-x))。Sigmoid函数的输出在0到1之间，它能将一个实数映射到一个"概率"值，因此经常被用在二分类问题的最后一层。但Sigmoid函数有一个主要问题是它在输入的绝对值较大时，梯度接近于0，这会导致神经网络训练时的梯度消失问题。

sigmoid主要有两个缺点：

1. 梯度饱和，看图可知，两边数值的梯度都为0；
2. 结果的平均值不为0，这是我们不希望的，因为这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。
   

tanh（Hyperbolic Tangent）函数
tanh函数是Sigmoid函数的变体，函数形式为 f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))。tanh函数的输出在-1到1之间，因此它的输出均值是0，这使得数据在经过tanh函数处理后能更好地符合处理神经网络输入的常用前提假设。tanh函数相比Sigmoid函数有更强的表达力，但仍然存在梯度消失的问题。

ReLU（Rectified Linear Unit）函数
ReLU是近年来在深度学习领域中使用最广泛的激活函数，函数形式为 f(x) = max(0, x)。ReLU函数在x大于0时保持原值，在x小于0时输出0，这使得它在正区间内保持了线性的特性，而在负区间则完全不激活。ReLU函数相比Sigmoid函数计算更简单，也在很大程度上缓解了梯度消失的问题，但ReLU的输出并不是限定在固定范围内，而且负数部分完全不激活可能导致某些神经元永久性失活。

Leaky ReLU、Parametric ReLU、ELU（Exponential Linear Units）等
这些都是ReLU函数的改进版本，它们在x小于0时，不再简单地输出0，而是输出一个较小的负值或根据x的值变化的负值，从而在一定程度上解决了ReLU的部分问题。

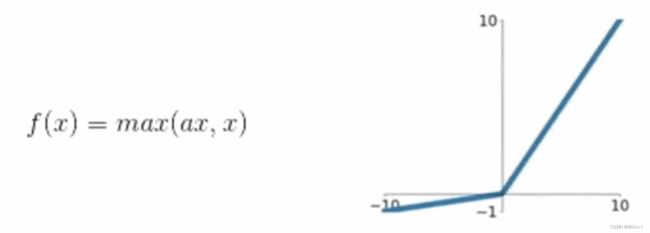
总结

2.4 神经元稀疏

神经元稀疏性（Neuron Sparsity）是指在神经网络中，仅有少数神经元对最终的输出产生贡献，或者说，在某个时间点，只有部分神经元被激活。这种现象通常通过使用具有稀疏性质的激活函数（如ReLU）实现，ReLU函数将所有负输入都映射到0，这使得很多神经元的输出为0，因此神经网络的激活变得稀疏。

神经元稀疏性有几个重要的好处：

1. 计算效率：因为大部分神经元的激活值为0，这样在计算过程中，我们可以跳过这些神经元，从而节省大量的计算资源。
2. 提高模型泛化能力：稀疏性可以作为一种正则化手段，它可以帮助模型集中关注输入特征的重要部分，防止模型过拟合。
3. 模型解释性：稀疏性使得模型的输出只依赖于少数几个输入特征，这有助于我们理解模型的决策过程。

然而，过度的稀疏性可能会导致信息丢失，使模型性能下降。因此，在实际应用中，需要找到合适的稀疏性平衡点。这也是为什么在很多深度学习模型中，会采用L1正则化、Dropout等方法来控制模型的稀疏性。

这种稀疏有何作用，为什么要让神经元稀疏？

1. 增强模型的泛化能力：通过限制模型的复杂性（即，减少活跃神经元的数量），神经元稀疏性可以防止模型过度拟合训练数据。这是因为过拟合通常发生在模型过于复杂并尝试记忆训练数据，而非从数据中学习一般的规律时。稀疏性约束使模型只关注输入特征的重要部分，从而提高了模型的泛化能力。
2. 提高计算效率：对于大规模的深度学习模型，稀疏性可以显著提高计算效率，因为在任何特定时间，只有一小部分神经元需要更新。在前向传播和反向传播过程中，大多数神经元的激活值为零，因此我们可以忽略这部分的计算。
3. 增加模型的解释性：当神经元稀疏时，每个特定的预测或决策通常只依赖于少量的输入特征，而不是全部特征。这种特性使得模型的预测过程更易于理解和解释。
4. 模仿生物神经系统：在人脑中，任何时刻只有少数神经元处于活跃状态，这是一种高效的能量使用策略。这种观察也启发了深度学习中神经元稀疏性的研究。

3. 设计神经网络

3.1 设计思路

1. 使用神经网络训练数据之前，必须确定神经网络的层数，以及每层单元的个数
2. 特征向量在被传入输入层时通常要先标准化到0-1之间（为了加速学习过程）
3. 离散型变量可以被编码成每一个输入单元对应一个特征值可能赋的值 比如：特征值A可能取三个值（a0, a1, a2), 可以使用3个输入单元来代表A。 如果A=a0, 那么代表a0的单元值就取1, 其他取0；1，0，0 如果A=a1, 那么代表a1的单元值就取1，其他取0，以此类推 0,1,0
4. 神经网络既可以用来做分类（classification）问题，也可以解决回归（regression）问题
   （1）对于分类问题，如果是2类，可以用一个输出单元表示（0和1分别代表2类）；如果多于2类，则每 一个类别用一个输出单元表示 1 0 0 01 0
   （2）没有明确的规则来设计最好有多少个隐藏层，可以根据实验测试和误差以及精准度来实验并改进。

3.2 对隐含层的感性认识

让我们从一个问题开始，假如区分以下三张图片哪个是人脸，也就是人脸识别，神经网络模型应该 怎么建立呢？为了简单起见，输入层的每个节点代表图片的某个像素，个数为像素点的个数，输出 层简单地定义为一个节点，标示“是”还是”不是“。

那么隐含层怎么分析呢？ 我们先从感性地角度认识这个人脸识别问题，试着将这个问题分解为一些子 问题，比如：

• 在上方有头发吗？
• 在左上、右上各有一个眼睛吗？
• 在中间有鼻子吗？
• 在下方中间位置有嘴巴吗？
• 在左、右两侧有耳朵吗？
• …

假如对以上这些问题的回答，都是“yes”，或者大部分都是“yes”，那么可以判定是人脸，否则不是人脸。

以上每个子网络，还可以进一步分解为更小的问题，比如判断左上是一个眼睛吗的问题，可以分 解为：

• 有眼球吗？
• 有眼睫毛吗？
• 有虹膜吗？
• …

这个子网络还可以进一步分解，.一层又一层地分解，直到 回答的问题简单到能在一个单独的神经元上被回答。

4. 深度学习

4.1 什么是深度学习

• 传统的神经网络发展到了多隐藏层的情况，
• 具有多个隐藏层的神经网络被称为深度神经网络，基于深度神经网络的机器学习研究称 之为深度学习。
• 如果需要细化和区分区别，那么，深度神经网络可以理解为对传统多层网络进行了结构、 方法等方面的优化。
• 深度学习，就是多层人工神经网络

图像识别：像素->边缘->纹理->图形->局部->物体
文字识别：字符->词->词组->子句->句子->故事

4.2 推理和训练

**推理：**你训练好了一个模型，在训练数据集中表现良好，但是我们的期望是它可以对以前 没看过的图片进行识别。你重新拍一张图片扔进网络让网络做判断，这种图片就叫做现场数据（live data），如果现场数据的区分准确率非常高，那么证明你的网络训练的是非常好的。这个过程，称为推理 （Inference）。

**训练：**一个初始神经网络通过不断的优化自身参数，来让自己变得准确。这整个过程就称之 为训练（Traning）。

4.3 训练的相关概念

深度学习的根本问题是优化和泛化之间的对立。

• 优化（optimization）是指调节模型以在训练数据上得到最佳性能（即机器学习中的学习）。
• 泛化（generalization）是指训练好的模型在前所未见的数据上的性能好坏。

数据集的分类：
数据集可以分为：

1. 训练集：实际训练算法的数据集；用来计算梯度，并确定每次迭代中网络权值的更新；
2. 验证集：用于跟踪其学习效果的数据集；是一个指示器，用来表明训练数据点之间所形成的网络函 数发生了什么，并且验证集上的误差值在整个训练过程中都将被监测；
3. 测试集：用于产生最终结果的数据集 。

为了让测试集能有效反映网络的泛化能力：

1. 测试集绝不能以任何形式用于训练网络，即使是用于同一组备选网络中挑选网络。测试集只能在所有的训练和模型选择完成后使用；
2. 测试集必须代表网络使用中涉及的所有情形。

交叉验证
这里有一堆数据，我们把他切成3个部分（当然还可以分的更多）
第一部分做测试集，二三部分做训练集，算出准确度；
第二部分做测试集，一三部分做训练集，算出准确度；
第三部分做测试集，一二部分做训练集，算出准确度；
之后算出三个准确度的平局值，作为最后的准确度。

代(Epoch)：使用训练集的全部数据对模型进行一次完整训练，被称为“一代训练”。

批大小(Batch size)：使用训练集的一小部分样本对模型权重进行一次反向传播的参数更新，这一小部分 样本被称为“一批数据”

迭代(Iteration)：使用一个Batch数据对模型进行一次参数更新的过程，被称为“一次训练”（一次迭代）。 每一次迭代得到的结果都会被作为下一次迭代的初始值。一个迭代=一个正向通过加一个反向通过。

比如训练集有500个样本，batchsize = 10 ，那么训练完整个样本集：iteration=50，epoch=1.

4.4 BP神经网络

BP神经网络，即反向传播神经网络，是一种基于误差反向传播算法的多层前馈神经网络。这种网络主要包括输入层、隐藏层和输出层三部分，各层之间的节点（神经元）通过权重连接。

下面是BP神经网络工作的基本步骤：

1. 前向传播：首先，将输入数据送入输入层，然后逐层（从输入层至隐藏层，最后至输出层）进行计算并传递。每一个神经元的输出是其所有输入的加权和，经过一个激活函数后得到的。
2. 计算误差：在输出层获取到网络的预测输出后，我们会计算预测输出与实际输出之间的差异（通常通过一个损失函数来计算）。
3. 反向传播误差：然后，我们将这个差异反向传播到网络中的每一层，用来更新每一层中的权重。这一过程的目标是使得网络的预测输出更接近实际输出。
4. 权重更新：在反向传播的过程中，我们会使用梯度下降或者其他优化算法，根据反向传播的误差来调整网络中的权重，从而最小化损失函数。

这个过程会在训练数据上反复进行，直到网络的性能达到预定的标准，或者经过预定的迭代次数。反向传播算法的提出是神经网络发展的一个重要里程碑，它有效地解决了多层神经网络中权重调整的问题，使得神经网络的应用得到了广泛推广。

# coding:utf8

import torch
import torch.nn as nn
import numpy as np
import copy

"""
基于pytorch的网络编写
手动实现梯度计算和反向传播
加入激活函数
"""


class TorchModel(nn.Module):
    def __init__(self, hidden_size):
        super(TorchModel, self).__init__()
        self.layer = nn.Linear(hidden_size, hidden_size, bias=False)
        self.activation = torch.sigmoid
        self.loss = nn.functional.mse_loss  # loss采用均方差损失

    # 当输入真实标签，返回loss值；无真实标签，返回预测值
    def forward(self, x, y=None):
        y_pred = self.layer(x)
        y_pred = self.activation(y_pred)
        if y is not None:
            return self.loss(y_pred, y)
        else:
            return y_pred


# 自定义模型，接受一个参数矩阵作为入参
class DiyModel:
    def __init__(self, weight):
        self.weight = weight

    def forward(self, x, y=None):
        y_pred = np.dot(self.weight, x)
        y_pred = self.diy_sigmoid(y_pred)
        if y is not None:
            return self.diy_mse_loss(y_pred, y)
        else:
            return y_pred

    # sigmoid
    def diy_sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    # 手动实现mse，均方差loss
    def diy_mse_loss(self, y_pred, y_true):
        return np.sum(np.square(y_pred - y_true)) / len(y_pred)

    # 手动实现梯度计算
    def calculate_grad(self, y_pred, y_true, x):
        # 前向过程
        # wx = np.dot(self.weight, x)
        # sigmoid_wx = self.diy_sigmoid(wx)
        # loss = self.diy_mse_loss(sigmoid_wx, y_true)
        # 反向过程
        # 均方差函数 (y_pred - y_true) ^ 2 / n 的导数 = 2 * (y_pred - y_true) / n
        grad_loss_sigmoid_wx = 2/len(x) * (y_pred - y_true)
        # sigmoid函数 y = 1/(1+e^(-x)) 的导数 = y * (1 - y)
        grad_sigmoid_wx_wx = y_pred * (1 - y_pred)
        # wx对w求导 = x
        grad_wx_w = x
        # 导数链式相乘
        grad = grad_loss_sigmoid_wx * grad_sigmoid_wx_wx
        grad = np.dot(grad.reshape(len(x), 1), grad_wx_w.reshape(1, len(x)))
        return grad

# 梯度更新


def diy_sgd(grad, weight, learning_rate):
    return weight - learning_rate * grad

# adam梯度更新


def diy_adam(grad, weight):
    # 参数应当放在外面，此处为保持后方代码整洁简单实现一步
    alpha = 1e-3  # 学习率
    beta1 = 0.9  # 超参数
    beta2 = 0.999  # 超参数
    eps = 1e-8  # 超参数
    t = 0  # 初始化
    mt = 0  # 初始化
    vt = 0  # 初始化
    # 开始计算
    t = t + 1
    gt = grad
    mt = beta1 * mt + (1 - beta1) * gt
    vt = beta2 * vt + (1 - beta2) * gt ** 2
    mth = mt / (1 - beta1 ** t)
    vth = vt / (1 - beta2 ** t)
    weight = weight - (alpha / (np.sqrt(vth) + eps)) * mth
    return weight


x = np.array([1, 2, 3, 4])  # 输入
y = np.array([0.1, -0.1, 0.01, -0.01])  # 预期输出

# torch实验
torch_model = TorchModel(len(x))
torch_model_w = torch_model.state_dict()["layer.weight"]
print(torch_model_w, "初始化权重")
numpy_model_w = copy.deepcopy(torch_model_w.numpy())
# numpy array -> torch tensor, unsqueeze的目的是增加一个batchsize维度
torch_x = torch.from_numpy(x).float().unsqueeze(0)
torch_y = torch.from_numpy(y).float().unsqueeze(0)
# torch的前向计算过程，得到loss
torch_loss = torch_model(torch_x, torch_y)
print("torch模型计算loss：", torch_loss)
# #手动实现loss计算
diy_model = DiyModel(numpy_model_w)
diy_loss = diy_model.forward(x, y)
print("diy模型计算loss：", diy_loss)

# #设定优化器
learning_rate = 0.1
optimizer = torch.optim.SGD(torch_model.parameters(), lr=learning_rate)
# optimizer = torch.optim.Adam(torch_model.parameters())
optimizer.zero_grad()
#
# #pytorch的反向传播操作
torch_loss.backward()
print(torch_model.layer.weight.grad, "torch 计算梯度")  # 查看某层权重的梯度

# #手动实现反向传播
grad = diy_model.calculate_grad(diy_model.forward(x), y, x)
print(grad, "diy 计算梯度")
#
# #torch梯度更新
# optimizer.step()
# #查看更新后权重
# update_torch_model_w = torch_model.state_dict()["layer.weight"]
# print(update_torch_model_w, "torch更新后权重")
#
# #手动梯度更新
# diy_update_w = diy_sgd(grad, numpy_model_w, learning_rate)
# diy_update_w = diy_adam(grad, numpy_model_w)
# print(diy_update_w, "diy更新权重")

4.5 训练的步骤及涉及的问题

1. 提取特征向量作为输入。选择样本集合的一个样本（Ai，Bi），Ai为数据、Bi为标签（所属类别）
2. 定义神经网络结构。包括隐藏层数，激活函数等等。送入网络，计算网络的实际输出Y，（此时网络中的权重应该都是随机量）
3. 通过训练利用反向传播算法不断优化权重的值，使之达到最合理水平。计算D=Bi−Y（即预测值与实际值相差多少）
4. 使用训练好的神经网络来预测未知数据(推理)，这里训练好的网络就是指权重达到最优的情 况。

参数的随机初始化

• 对于所有的参数我们必须初始化它们的值，而且它们的初始值不能设置成一样，比如都设置成0或1。 如果设置成一样那么更新后所有参数都会相等。即所有神经元的功能都相等，造成了高度冗余。所 以我们必须随机化初始参数。
• 特别的，如果神经网络没有隐藏层，则可以把所有参数初始化为0。（但这也不叫深度神经网络了）

标准化（Normalization）
原因：由于进行分类器或模型的建立与训练时，输入的数据范围可能比较大，同时样本中各数据可 能量纲不一致，这样的数据容易对模型训练或分类器的构建结果产生影响，因此需要对其进行标准 化处理，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行 比较和加权。

其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。

z-score标准化（零均值归一化zero-mean normalization）：

• 经过处理后的数据均值为0，标准差为1（正态分布）
• 其中μ是样本的均值， σ是样本的标准差

import numpy as np
import matplotlib.pyplot as plt
#归一化的两种方式
def Normalization1(x):
    '''归一化（0~1）'''
    '''x_=(x−x_min)/(x_max−x_min)'''
    return [(float(i)-min(x))/float(max(x)-min(x)) for i in x]
def Normalization2(x):
    '''归一化（-1~1）'''
    '''x_=(x−x_mean)/(x_max−x_min)'''
    return [(float(i)-np.mean(x))/(max(x)-min(x)) for i in x]
#标准化
def z_score(x):
    '''x∗=(x−μ)/σ'''
    x_mean=np.mean(x)
    s2=sum([(i-np.mean(x))*(i-np.mean(x)) for i in x])/len(x)
    return [(i-x_mean)/s2 for i in x]
 
l=[-10, 5, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 15, 15, 30]
l1=[]
# for i in l:
#     i+=2
#     l1.append(i)
# print(l1)
cs=[]
for i in l:
    c=l.count(i)
    cs.append(c)
print(cs)
n=Normalization2(l)
z=z_score(l)
print(n)
print(z)
'''
蓝线为原始数据，橙线为z
'''
plt.plot(l,cs)
plt.plot(z,cs)
plt.show()

正向传播
输入信号从输入层经过各个隐藏层向输出层传播。在输出层得到实际的响应值，若实际值与期 望值误差较大，就会转入误差反向传播阶段。
反向传播
按照梯度下降的方法从输出层经过各个隐含层并逐层不断地调整各神经元的连接权值和阈值， 反复迭代，直到网络输出的误差减少到可以接受的程度，或者进行到预先设定的学习次数。

泛化能力分类

• 欠拟合：模型没有能够很好的表现数据的结构，而出现的拟合度不高 的情况。模型不能在训练集上获得足够低的误差；
• 拟合：测试误差与训练误差差距较小；
• 过拟合：模型过分的拟合训练样本，但对测试样本预测准确率不高的 情况，也就是说模型泛化能力很差。训练误差和测试误差之间的差距 太大；
• 不收敛：模型不是根据训练集训练得到的。

过拟合出现的原因：

1. 建模样本选取了错误的选样方法、样本标签等，或样本数量太少，所选取的样本数据不足以代表预 定的分类规则
2. 样本噪音干扰过大，使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
3. 假设的模型无法合理存在，或者说是无法达到假设成立的条件
4. 参数太多导致模型复杂度过高
5. 对于神经网络模型：a)对样本数据可能存在分类决策面不唯一，随着学习的进行,，BP算法使权值可 能收敛过于复杂的决策面；b)权值学习迭代次数足够多，拟合了训练数据中的噪声和训练样例中没有代 表性的特征。

过拟合的解决方法：

1. 减少特征：删除与目标不相关特征，如一些特征选择方法
2. Early stopping
3. 更多的训练样本。
4. 重新清洗数据。
5. Dropout

Early Stopping：

• 在每一个Epoch结束时，计算validation data的accuracy，当accuracy不再提高时，就停止训练。
• 那么该做法的一个重点便是怎样才认为validation accurary不再提高了呢？并不是说validation accuracy一降下来便认为不再提高了，因为可能经过这个Epoch后，accuracy降低了，但是随后的 Epoch又让accuracy又上去了，所以不能根据一两次的连续降低就判断不再提高。
• 一般的做法是，在训练的过程中，记录到目前为止最好的validation accuracy，当连续10次Epoch （或者更多次）没达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了 （Early Stopping）。
• 这种策略也称为“No-improvement-in-n”，n即Epoch的次数，可以根据实际情况取，如10、20、30

Dropout：
在神经网络中，dropout方法是通过修改神经网络本身结构来实现的：

1. 在训练开始时，随机删除一些（可以设定为1/2，也可以为1/3，1/4等）隐藏层神经元，即 认为这些神经元不存在，同时保持输入层与输出层神经元的个数不变。
2. 然后按照BP学习算法对ANN中的参数进行学习更新（虚线连接的单元不更新，因为认为这 些神经元被临时删除了）。这样一次迭代更新便完成了。下一次迭代中，同样随机删除一 些神经元，与上次不一样，做随机选择。这样一直进行，直至训练结束。

Dropout方法是通过修改ANN中隐藏层的神经元个数来防止ANN的过拟合。

为什么Dropout能够减少过拟合：

1. Dropout是随机选择忽略隐层节点，在每个批次的训练过程，由于每次随机忽略的隐层节点都不同， 这样就使每次训练的网络都是不一样的， 每次训练都可以当做一个“新”模型；
2. 隐含节点都是以一定概率随机出现，因此不能保证每2个隐含节点每次都同时出现。

这样权值的更新不再依赖有固定关系隐含节点的共同作用，阻止了某些特征仅仅在其他特定特征下才有 效果的情况。

总结：Dropout是一个非常有效的神经网络模型平均方法，通过训练大量的不同的网络，来平均预测概 率。不同的模型在不同的训练集上训练（每个epoch的训练数据都是随机选择），最后在每个模型用相 同的权重来“融合”。

4.6 损失函数

在机器学习和深度学习中，损失函数（或称为代价函数或目标函数）是一个非常关键的概念。它用于量化预测值与真实值之间的差异，即模型的预测错误程度。

这里列举一些常见的损失函数：

1. 均方误差（Mean Squared Error, MSE）：这是回归问题中最常用的损失函数。公式为：MSE = 1/n Σ(yi - ŷi)^2，其中yi代表真实值，ŷi代表预测值，n为样本数量。MSE衡量了模型预测值与实际值差值的平方的平均数，由于采用了平方，所以对于大的误差，其惩罚更大。
2. 交叉熵损失（Cross-Entropy Loss）：这是分类问题中常用的损失函数，特别是二分类和多分类问题。交叉熵损失衡量的是模型预测概率分布与真实分布之间的差异。对于二分类问题，交叉熵损失的公式为：- Σ [yi log(ŷi) + (1 - yi) log(1 - ŷi)]。
3. 绝对值误差（Mean Absolute Error, MAE）：这是另一个用于回归问题的损失函数，它直接衡量了预测值和实际值之间的平均绝对差异。MAE的计算公式为：MAE = 1/n Σ|yi - ŷi|。
4. Hinge损失：这是用于支持向量机（SVM）和一些线性分类问题的损失函数。它不仅关注分类是否正确，还关注分类的“置信度”。
5. 对数损失（Log Loss）：对数损失通常用于二分类问题，是交叉熵损失的特例。与交叉熵损失相同，它也是用于衡量模型预测概率分布与真实分布之间的差异。

损失函数的选取取决于输入标签数据的类型：

1. 如果输入的实数、无界的值，损失函数使用MSE。
2. 如果输入标签是位矢量（分类标志），使用交叉熵会更适合。

4.7梯度下降算法

梯度下降算法是一种最优化算法，用于最小化函数，例如在神经网络或任何机器学习算法中最小化损失函数。它的工作原理是：首先计算损失函数的梯度，然后选择一个步长，将参数朝着梯度的反方向移动一步，以减小损失函数的值。这个过程会反复进行，直到达到一个局部最小值。

• 梯度∇f=(∂x1∂f;∂x2∂f;…;∂xn∂f)指函数关于变量x的导数，梯度的方向表示函数值增大的方向，梯度的 模表示函数值增大的速率。
• 那么只要不断将参数的值向着梯度的反方向更新一定大小，就能得到函数的最小值（全局最小值或 者局部最小值）。
• 一般利用梯度更新参数时会将梯度乘以一个小于1的学习速率（learning rate），这是因为往往梯度 的模还是比较大的，直接用其更新参数会使得函数值不断波动，很难收敛到一个平衡点（这也是学 习率不宜过大的原因）。
  

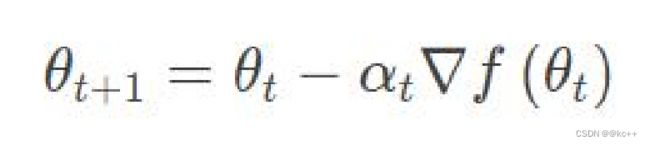
学习率
学习率是一个重要的超参数，它控制着我们基于损失梯度调整神经网络权值的速度。

学习率越小，我们沿着损失梯度下降的速度越慢。

从长远来看，这种谨慎慢行的选择可能还不错，因为可以避免错过任何局部最优解，但它也意味 着我们要花更多时间来收敛，尤其是如果我们处于曲线的至高点。

新权值 = 当前权值 - 学习率 × 梯度

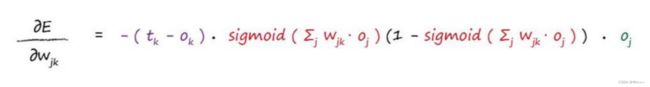
紫色部分：正确结果与节点输出结果的差值，也就是误差;
红色部分：节点的激活函数，所有输入该节点的链路把经过其上的信号与链路权重做乘积后加总，再把加总结 果进行激活函数运算;
绿色部分：链路w(jk)前端节点输出的信号值。

import matplotlib.pyplot as pyplot
import math

# X = [0.01 * i for i in range(100)]
# Y = [2 * x ** 2 + 3 * x + 4 for x in X]
# print(X)
# print(Y)
# pyplot.scatter(X, Y)
# pyplot.show()

X = [0.0, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.19, 0.2, 0.21, 0.22, 0.23, 0.24, 0.25, 0.26, 0.27, 0.28, 0.29, 0.3, 0.31, 0.32, 0.33, 0.34, 0.35000000000000003, 0.36, 0.37, 0.38, 0.39, 0.4, 0.41000000000000003, 0.42, 0.43, 0.44, 0.45, 0.46, 0.47000000000000003, 0.48, 0.49, 0.5, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.5700000000000001, 0.58, 0.59, 0.6, 0.61, 0.62, 0.63, 0.64, 0.65, 0.66, 0.67, 0.68, 0.6900000000000001, 0.7000000000000001, 0.71, 0.72, 0.73, 0.74, 0.75, 0.76, 0.77, 0.78, 0.79, 0.8, 0.81, 0.8200000000000001, 0.8300000000000001, 0.84, 0.85, 0.86, 0.87, 0.88, 0.89, 0.9, 0.91, 0.92, 0.93, 0.9400000000000001, 0.9500000000000001, 0.96, 0.97, 0.98, 0.99]
Y = [4.0, 4.0302, 4.0608, 4.0918, 4.1232, 4.155, 4.1872, 4.2198, 4.2528, 4.2862, 4.32, 4.3542, 4.3888, 4.4238, 4.4592, 4.495, 4.5312, 4.5678, 4.6048, 4.6422, 4.68, 4.7181999999999995, 4.7568, 4.7958, 4.8352, 4.875, 4.9152000000000005, 4.9558, 4.9968, 5.0382, 5.08, 5.122199999999999, 5.1648, 5.2078, 5.2512, 5.295, 5.3392, 5.3838, 5.4288, 5.4742, 5.5200000000000005, 5.5662, 5.6128, 5.6598, 5.7072, 5.755, 5.8032, 5.851800000000001, 5.9008, 5.9502, 6.0, 6.0502, 6.1008, 6.1518, 6.203200000000001, 6.255000000000001, 6.3072, 6.3598, 6.4128, 6.4662, 6.52, 6.5742, 6.6288, 6.6838, 6.7392, 6.795, 6.8512, 6.9078, 6.9648, 7.022200000000001, 7.08, 7.138199999999999, 7.1968, 7.2558, 7.3152, 7.375, 7.4352, 7.4958, 7.5568, 7.6182, 7.680000000000001, 7.7422, 7.8048, 7.867800000000001, 7.9312, 7.994999999999999, 8.0592, 8.1238, 8.1888, 8.2542, 8.32, 8.3862, 8.4528, 8.5198, 8.587200000000001, 8.655000000000001, 8.7232, 8.7918, 8.8608, 8.9302]


def func(x):
    return w1 * x ** 2 + w2 * x + w3


def loss(y_pred, y_true):
    return (y_pred - y_true) ** 2

# 权重随机初始化
w1, w2, w3 = -1, 1, 0

# 学习率
lr = 0.01

for epoch in range(10000):
    epoch_loss = 0
    for x, y_true in zip(X, Y):
        y_pred = func(x)
        epoch_loss += loss(y_pred, y_true)
        #梯度计算
        grad_w1 = 2 * (y_pred - y_true) * x ** 2
        grad_w2 = 2 * (y_pred - y_true) * x
        grad_w3 = 2 * (y_pred - y_true)
        #根据梯度修改权重（优化器）
        w1 = w1 - lr * grad_w1
        w2 = w2 - lr * grad_w2
        w3 = w3 - lr * grad_w3

    epoch_loss /= len(X)
    print("第%d轮， loss %f" %(epoch, epoch_loss))
    if epoch_loss < 0.01:
        break

print("训练后权重:", w1, w2, w3)


Y1 = [func(i) for i in X]

# pyplot.scatter(X, Y, color="red")
# pyplot.scatter(X, Y1)
# pyplot.show()

5. 神经网络训练过程实例

1. 第一层是输入层，包含两个神 经元：i1，i2 和偏置b1；
2. 第二层是隐藏层，包含两个神 经元：h1，h2 和偏置项b2；
3. 第三层是输出：o1，o2。
4. 每条线上标的 wi 是层与层之间 连接的权重。
5. 激活函数是 sigmod 函数。
6. 我们用 z 表示某神经元的加权 输入和；用 a 表示某神经元的 输出。

5.1 step1 – 前向传播

输入层 —> 隐藏层



隐藏层 —> 输出层

5.2 step2 – 反向传播

这样，反向传播算法就完成了，最后我们再把更新的权值重新计算，不停地迭代。
在这个例子中第一次迭代之后，总误差0.298371109下降至0.291027924。
迭代10000次后，总误差为0.000035085。输出为：[0.015912196, 0.984065734]

6. softmax

Softmax函数是一种在机器学习（尤其是深度学习）中常用的激活函数，主要用于多分类问题中。Softmax函数可以将一个含任意实数的K维向量“压缩”到另一个K维实向量中，使得每一个元素的范围都在(0,1)之间，并且所有元素的和为1。这样的性质使得Softmax函数的输出可以被解释为概率分布。

假设我们有一个K维的向量z，z的第i个元素记作z_i。那么，z的Softmax函数的输出的第i个元素可以计算为：

S(z)_i = exp(z_i) / Σ_j exp(z_j)

其中，"exp"是指数函数，Σ_j表示对所有的j进行求和。

Softmax函数的这种性质使得它在多分类问题中特别有用，我们可以将神经网络的输出经过Softmax函数处理，然后取最大的那个元素对应的类别作为预测的类别。同时，由于Softmax函数的输出可以被解释为概率分布，我们也可以容易地得到模型对每个类别的预测概率。

需要注意的是，虽然Softmax函数可以将输出转化为概率分布，但这并不意味着使用Softmax函数就可以得到良好的分类效果。模型的训练过程、网络的结构、损失函数的选择等因素都对最终的分类效果有影响。

7.用Keras实现一个简单神经网络

Keras：
Keras是由纯python编写的基于theano/tensorflow的深度学习框架。
Keras是一个高层神经网络API，支持快速实验，能够把你的idea迅速转换为结果，如果有如下需求，可以优先选择Keras：
a）简易和快速的原型设计（keras具有高度模块化，极简，和可扩充特性）
b）支持CNN和RNN，或二者的结合
c）无缝CPU和GPU切换

from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense

# 创建模型
model = Sequential()

# 添加第一层卷积层和最大池化层
model.add(Conv2D(32, (3, 3), activation='relu', input_shape=(64, 64, 3)))
model.add(MaxPooling2D(pool_size=(2, 2)))

# 添加第二层卷积层和最大池化层
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))

# 展平数据
model.add(Flatten())

# 添加全连接层
model.add(Dense(128, activation='relu'))

# 添加输出层
model.add(Dense(10, activation='softmax'))

# 编译模型，使用交叉熵作为损失函数，梯度下降作为优化器
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

# 训练模型，这里用'X_train'和'y_train'代表训练数据和标签，'X_val'和'y_val'代表验证数据和标签
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_val, y_val))

# 打印训练过程中的损失值和准确率
print(history.history)