2023年第十四届蓝桥杯JavaB组省赛真题及解析

前言：

---

本次比赛我只能说真是技不如人，本以为精通暴力算法就能狠狠拿下蓝桥杯的我，真的是被狠狠军训了。虽然最后也是拿了二等安慰奖，但是内心根本没有多开心，因为自己这几个月学的算法，几乎没有在本次比赛发挥作用，而且一直处于被题目吊打的局面。但这不能说明刷题没用，只能说我的水平还有待提高。

这里不得不再次总结蓝桥杯的重要特点：重心态，重思维。

想想也是如果单纯以刷题量衡量能否在蓝桥杯取得好成绩是不妥当的。毕竟大一，大二乃至大三都可以参加，单纯以刷题就能取得好成绩的话，对大一刚接触编程的新生来说太不利了，所以侧重思维就相对来说更公平。当然最后的心态也就不必多说了，乃至人生中都非常重要。

比赛的时候虽然啥也不会，但是我还能尽可能让自己冷静下来思考，毕竟该付出的都做了，我不会他们也不会。

最后也是因为冷静多做出来一道题，拿了安慰奖。遗憾的就是如果我能再冷静一点，再多去思考一下。真的就能再做出来一道题，可能就省一了，只能说太可惜，但失败的情理之中。再者，我总能在失败中学到点什么。

想要取得好成绩总结一下：

1.心态一定要好。

该做的都做了不管遇到什么情况，就坦然面对吧。

2.不要盲目刷题。

一定要多思考，一定多思考，理解算法本质。通过刷题锻炼思维，锻炼举一反三的能力。

3.最后也不要怕失败。

为别人的期待而活真的很累，简单点为自己而活吧。最后送上“足球诗人贺炜”的话：

人生当中成功只是一时的，失败却是主旋律，但是如何面对失败，却把人分成了不同的样子。有的人会被失败击垮，有的人能够不断地爬起来，不断向前，我想真正的成熟并不是追求完美，而是直面自己的缺憾这才是生活的本质。

---

蓝桥杯题目：

最后就是最近太忙了，成块的时间太少了，本博客会分片持续更新的。

想要自己做做真题的话点这里：2023年第十四届蓝桥杯JavaB组省赛真题

—— 2023.5.14

---

A、阶乘求和：

【问题描述】

令 S = 1! + 2! + 3! + … + 202320232023! ，
求 S 的末尾 9 位数字。
提示：答案首位不为 0 。

答案：420940313

这道题虽然短但确实虎住我了我当时一心想着要把这个数完整的算出来，结果爆了long就不会了，也想到用Java的 BigInteger 但是时间不够了。当时真是死脑筋，晓得随着阶乘的增加后面的数会固定，当时还想着用规律推出来，真是太sb了。

真正的解法其实很简单 mod 10^9 就行，他要看后面九个数，咱就只考虑后面九个数即可，当时真是没想到 mod。
即 / 10^9考虑前九位，% 10^9保留后9位可见我对这个掌握还是不到位，比赛的时候居然想不到。

1.朴素代码：

import java.util.*;

public class Main {
	
	public static long INF = 10000000000L;
	
	public static void main(String[] args) {
		long sum = 0;
		for(int i = 1; i <= 40; i ++)  {
			 sum = sum + fact(i);
		}
		System.out.println(sum % 1000000000);
    }
	public static long fact(int n) {
		long sum1 = 1;
		for(long i = 1; i <= n; i ++) {
			sum1 = sum1 * i;
			if(sum1 >= INF) sum1 = sum1 % INF;
		}
		return sum1;
	}
}

2. java自带BigInteger解：

import java.math.BigInteger;
 
public class Main {
	public static void main(String[] args) {
		 BigInteger sum = BigInteger.valueOf(0);//初始化0 
		 for(int i = 1; i <= 40; i ++) { 
			 BigInteger sum1 = BigInteger.valueOf(1);
			 for(int j = 1; j <= i; j ++) {
				 sum1 = sum1.multiply(BigInteger.valueOf(j));//乘法
			 }
			 sum = sum.add(sum1);
		 }
		 System.out.println(sum);//最后复制最后九位数即是答案。
	} 
}

———— 2023.5.14

---

B、幸运数字：

【问题描述】

哈沙德数是指在某个固定的进位制当中，可以被各位数字之和整除的正整 数。例如 126 是十进制下的一个哈沙德数，因为 (126) 10 mod
(1+2+6) = 0 ； 126 也是八进制下的哈沙德数，因为 (126) 10 = (176) 8 ， (126) 10 mod (1 + 7 + 6) = 0 ； 同时 126 也是 16 进制下的哈沙德数，因为 (126) 10 = (7 e ) 16 ， (126) 10 mod (7 + e ) = 0 。小蓝认为，如果一个整数在二进制、八进制、十进制、十六进制下均为
哈沙德数，那么这个数字就是幸运数字，第 1 至第 10 个幸运数字的十进制表示 为：1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数 字是多少？你只需要告诉小蓝这个整数的十进制表示即可。

答案：215040

这道题我最开始想的是想找到规律，很显然没有鸟用果然高端的比赛往往只需要最朴素的做题方式。

本题就考的进制转换问题，要将十进制5转换成二进制，通过%2,和/2的交替使用即可完成，所得余数就是转换成的二进制各位的值，转换成其他进制也是类似，就是重复部分很多，搞点分不容易。

代码：

public class Main {
	public static void main(String[] args) {
		  int cnt = 0;
		  int i = 1;
		  while(true) {
			  if(i % get_n(i, 2) == 0 && i % get_n(i, 8) == 0 && i % get_n(i, 10) == 0 && i % get_n(i, 16) == 0) cnt ++;
			  if(cnt == 2023)break;
			  i ++;
		  }
		  System.out.println(i);
	}
	public static int get_n(int n, int binary) {
		int sum = 0;
		while(n > 0) {
			sum = sum + n % binary;
			n = n / binary;
		}
		return sum;
	}
}

当然Java还自带进制转换函数，也可以用那个解，我记不住，就不写了。

———— 2023.5.15

---

C、数组分割：

[题目描述]

小蓝有一个长度为 N 的数组 A = [A0, A1,…, AN−1]。现在小蓝想要从 A 对应的数组下标所构成的集合 I = {0,
1, 2, . . . , N − 1} 中找出一个子集 R1，那么 R1在 I 中的补集为 R2。记 S1=∑r∈R1Ar，S2
=∑r∈R2Ar，我们要求 S1 和 S2 均为偶数，请问在这种情况下共有多少种不同的 R1。当 R1 或 R2 为空集时我们将 S1 或 S2 视为 0。 输入格式 第一行一个整数 T，表示有 T 组数据。 接下来输入 T 组数据，每组数据包含两行：第一行一个整数 N，表示数组
A 的长度；第二行输入 N 个整数从左至右依次为 A0, A1, . . . , AN−1，相邻元素之间用空格分隔。 输出格式
对于每组数据，输出一行，包含一个整数表示答案，答案可能会很大，你需要将答案对1000000007 进行取模后输出。

样例输入:

2
2
6 6
2
1 6

样例输出:

4
0

[提示]
对于第一组数据，答案为 4。（注意：大括号内的数字表示元素在数组中的下标。）
R1 = {0}, R2 = {1}；此时 S1 = A0 = 6 为偶数, S2 = A1 = 6 为偶数。
R1 = {1}, R2 = {0}；此时 S1 = A1 = 6 为偶数, S2 = A0 = 6 为偶数。
R1 = {0, 1}, R2 = {}；此时 S1 = A0 + A1 = 12 为偶数, S2 = 0 为偶数。
R1 = {}, R2 = {0, 1}；此时 S1 = 0 为偶数, S2 = A0 + A1 = 12 为偶数。
对于第二组数据，无论怎么选择，都不满足条件，所以答案为 0。

对于 20% 的评测用例，1 ≤ N ≤ 10。
对于 40% 的评测用例，1 ≤ N ≤ 102。
对于 100% 的评测用例，1 ≤ T ≤ 10, 1 ≤ N ≤ 103 , 0 ≤ Ai ≤ 109。

解题：

解题…解题这道题是坑的我最惨的一道题，初次看这道题，我一口便咬定这是一道动态规划题。
窃喜的同时心里也是一顿咒骂，小小桥杯居然第三道就动态规划，真是不给一点喘息余地啊~
同时心里也在暗喜，毕竟考式之前可把 数组切分 给拿捏了，这两道题光是名字都及其相似，那么解法肯定差不了哪去管着先用暴力先拿70%得分数，再用备忘录拿剩下的30%的想法，简直游刃有余…

当我写出代码准备测试的时候，我突然惊厥，把一个数组分成两个子数组 R1，R2，如果下标为0，1的子元素符合条件，那么{0，1}就是一种情况，但{1，0}就不能算进去，很不巧我的暴力解法，将两种情况都纳入了 我当时就直呼热烈的马，也就是说，我还得去重！怎么去？根本没法下手，本来代码就够长了（70多行） 再用Hashset，去重简直就是吃力不讨好（去重过程十分复杂），只能称作肉包子打狗。最后又垂S挣扎了20来分钟，我的代码只能通过元素个数为两个以下的测试案例,我直呼热烈的马！

这个故事告诉我们，题目给的样例一定要分析明了，清楚，不然写出来的代码只能过个样例，那就浪费表情了。

正解：

你敢信这道题居然是个排列组合问题？也就是咱高中学的什么 C(r, n) , A(m, n) 这类的。
思路如下：

1. 题目要保证 A 的子数组 R1, R2 的元素和都为 偶数

那么由 ：偶数 + 偶数 = 偶数 的定理。
可知 ：A 的元素和 也为偶数

2. 奇数 + 奇数 = 偶数

也可以理解为 ：偶数个奇数和 = 偶数

3. R1 和 R2 是相关联的，即我们只需要知道R1的情况，就可以以用A - R1,就能得到R2的情况

朴素的说就是我们只需要讨论R1就行

接下来就是讨论R1了：

我们知道A内的元素，有偶数，也有奇数，我们把所有偶数都放到A0集合，剩下所有奇数放到A1集合。

那么核心就来了：

想要 R1 内的元素和都为 偶数那么 R1可在A0中取任意个元素，但在A1集合里只能取偶数个元素，这样才能凑成偶数和。

所以研究的方向就变成了有多少种符合条件的上述取法。

假设A0内的元素个数为L, A1中的元素个数为 J (这个J必为偶数):

那么在A0中的取法 = ( 2 * 2 * 2 * 2 * 2… L个2) = 2 ^ L

由于A0内的都是偶数呗，每个元素就分取与不取两种情况喽。

那么在A1中的取法 = C(0, J) + C(2, J) + C(4, J) + … + C(J, J)

由于:
C(0, 0) = 1 = 2 ^ 0
C(0, 2) + C(2, 2) = 2 = 2 ^ 1
C(0, 4) + C(2, 4) + C(4, 4) = 8 = 2 ^ 3
.....

不难推出在A1中的取法 = 2 ^ (J - 1) 且 J > 0

4.所以总的方案数N = A0中的总选法 * A1中的总选法 = (2 ^ L) * [2 ^ (J - 1)]( 且 J > 0)

真是搞点分不容易啊!

正解代码：

import java.util.*;

public class Main {
    public static int mod = 1000000007;
	public static void main(String[] args) {
		 Scanner sc = new Scanner(System.in);
		 int n = sc.nextInt();
		 int a[];
		 while(n > 0) { 
			 int m = sc.nextInt();
			 a = new int[m];
			 for(int i = 0; i < m; i ++) a[i] = sc.nextInt();
			 int L = 0, J = 0;
			 
			 for(int i = 0; i < m; i ++) 
				 if(a[i] % 2 == 0) L ++;
				 else J ++;
			 
			 if(J % 2 != 0) System.out.println(0);
			 else {
				 if(J == 0) J = 1;
				 System.out.println((int)(Math.pow(2, L) * Math.pow(2, J - 1) % mod));
			 }
			 n --;
		 }
  }
}

本题思路来源：数组分割蓝桥杯java b组

———— 2023.5.18

---

D、矩形总面积:

[题目描述]

平面上有个两个矩形 R1 和 R2，它们各边都与坐标轴平行。设 (x1, y1) 和(x2, y2) 依次是 R1
的左下角和右上角坐标，(x3, y3) 和 (x4, y4) 依次是 R2 的左下角和右上角坐标，请你计算 R1 和 R2 的总面积是多少？
注意：如果 R1 和 R2 有重叠区域，重叠区域的面积只计算一次。 输入格式 输入只有一行，包含 8
个整数，依次是：x1，y1，x2，y2，x3，y3，x4 和 y4

输出格式:

一个整数，代表答案。

样例输入:

2 1 7 4 5 3 8 6

样例输出:

22

[提示]

样例中的两个矩形如图所示：

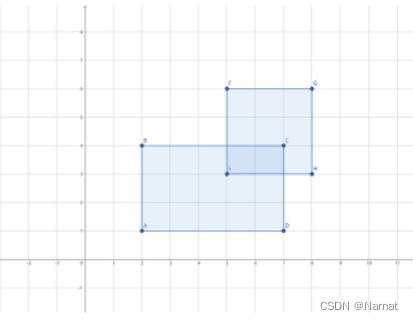
对于 20% 的数据，R1 和 R2 没有重叠区域。
对于 20% 的数据，其中一个矩形完全在另一个矩形内部。
对于 50% 的数据，所有坐标的取值范围是 [0, 10^3 ]。
对于 100% 的数据，所有坐标的取值范围是 [0, 10^5 ]。

解题：

这道题我是真不擅长我几乎都是做数组题目，他给的这个网格题我是真没咋做过，我最开始暴力一点的想法是整一个用数组代替这个平面，符合的范围标记上，最后查看该数组内的有多少被标记了，就是所要求矩形总面积。由于坐标最大取值为10^5所以数组由于开了过多空间会爆掉，还有就是矩阵的面积与所含空格数直接相关而设立的数组只能查符合条件的点数，矩阵相交的话，形成的面积与该区域所包含点的关系就不好明确了。

所以想完美解开这道题，就只能找规律咯, 我真是找不出来所以比赛的时候就是朴素的if else分情况讨论,太sb了就不放出来了。

这里直接就给正规解了：

1.如果两个矩阵相交了，那么相交的区域必然也是个矩阵

大家可以自己画图验证一下

2.找到相交区域矩阵的，左下角坐标和右上角坐标即可算出相交区域面积

假设相交区域,矩阵的左下角坐标为（m1, n1）,右上角坐标为（m2, n2）那么必然存在（直接给规律了）：

交集左下角端点可以表示为：
m1 = max(min(x1, x2), min(x3, x4));
n1 = max(min(y1, y2), min(y3, y4));
交集右上角端点可以表示为：
m2 = min(max(x1, x2), max(x3, x4));
n2 = min(max(y1, y2), max(y3, y4));

3.两个矩阵不相交，那么必然存在n2 < n1 && m2 < n1

注意：得用long , 因为10^5 * 10^5 会爆int。 知道矩阵左下角坐标和右上角坐标算面积应该
就非常好算了，直接（横坐标2 - 横坐标1）* （纵坐标2 - 纵坐标1）即可。

本题满分代码如下：

import java.util.*;

public class Main {
	 
	public static void main(String[] args) {
		 Scanner sc = new Scanner(System.in);
		 long a[] = new long[8];
		 for(int i = 0; i < 8; i ++) a[i] = sc.nextInt();
		 long m1 = 0, n1 = 0, m2 = 0, n2 = 0;
		 
		 m1 = Math.max(Math.min(a[0], a[2]), Math.min(a[4], a[6]));
		 n1 = Math.max(Math.min(a[1], a[3]), Math.min(a[5], a[7]));
		 
		 m2 = Math.min(Math.max(a[0], a[2]), Math.max(a[4], a[6]));
		 n2 = Math.min(Math.max(a[1], a[3]), Math.max(a[5], a[7]));
		 
		 long sum1 = 0;
		 
		 if(m2 > m1 && n2 > n1) sum1 = (m2 - m1) * (n2 -  n1);
		 
		 System.out.println((a[2] - a[0]) * (a[3] - a[1]) + (a[6] - a[4]) * (a[7] - a[5]) - sum1);
	}
}

本题解题思路来源：蓝桥杯基础练习（矩形面积交）

———— 2023.5.17

---