力扣刷题 - 数组篇
这里写目录标题
- 数组的遍历
-
- 485
- 495
- 414
- 628
- 统计数组中的元素
- 645
- 697
- 448
- 442
- 41
- 数组的改变与移动
-
- 453
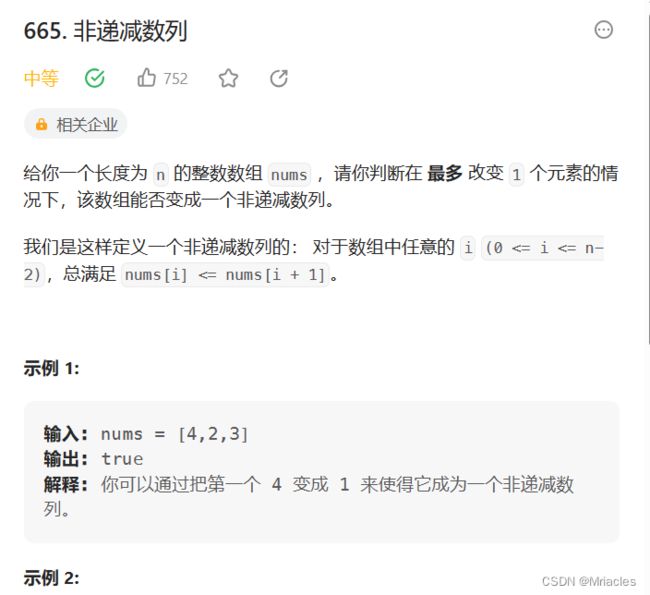
- 665---
- 283
- 二维数组以及滚动数组
-
- 118
- 119
- 661
- 419---
- 数组的旋转
-
- 189
- 396
- 特定顺序遍历二维数组
-
- 54
- 59
- 498
- 二维数组的变换
-
- 566
- 48
- 73---
- 前缀和数组
-
- 303
- 238
- 506
数组的遍历
485
https://leetcode.cn/problems/max-consecutive-ones/
public int findMaxConsecutiveOnes(int[] nums) {
int max=0;
int count=0;
for(int i=0; i < nums.length ;i++){
if(nums[i] == 1){
count++;
if(max < count){
max = count;
}
}else{
count=0;
}
}
return max;
}
495
https://leetcode.cn/problems/teemo-attacking/

暴力解法: 记录每次中的开始时间与结束时间, 然后如果下一次中毒的是在结束时间之前, 就去更新开始时间(让它加上这个持续时间减去结束时间),如果是在之后,直接加上持续时间
public int findPoisonedDuration(int[] timeSeries, int duration) {
int ans = 0;//开始时间
int expired = 0;//结束时间
for (int i = 0; i < timeSeries.length; ++i) {
if (timeSeries[i] >= expired) {
ans += duration;
} else {
ans += timeSeries[i] + duration - expired;
}
expired = timeSeries[i] + duration;
}
return ans;
}
414

注意,要求返回第三大的数,是指在所有不同数字中排第三大的数。
此例中存在两个值为 2 的数,它们都排第二。在所有不同数字中排第三大的数为 1 。
解法1 : 数组排序, 然后用哈希表找出不同数字中的第三大的数
public int thirdMax(int[] nums) {
Arrays.sort(nums);
if (nums.length < 3){
return nums[nums.length-1];
}
HashSet<Integer> set=new HashSet<>();
int k=0;
int max=0;
for (int i = nums.length-1; i >=0 ; i--) {
if (!set.contains(nums[i])){
set.add(nums[i]);
k++;
if (k == 3){
max=nums[i];
break;
}
}
}
if(k < 3){
return nums[nums.length-1];
}
return max;
}
解法2 : 用一个有序集合来维护数组中前三大的数。具体做法是每遍历一个数,就将其插入有序集合,若有序集合的大小超过 3,就删除集合中的最小元素。这样可以保证有序集合的大小至多为 3,且遍历结束后,若有序集合的大小为 3,其最小值就是数组中第三大的数;若有序集合的大小不足 3,那么就返回有序集合中的最大值。
public int thirdMax(int[] nums) {
TreeSet<Integer> s = new TreeSet<Integer>();
for (int num : nums) {
s.add(num);
if (s.size() > 3) {
s.remove(s.first());
}
}
return s.size() == 3 ? s.first() : s.last();
}
628
https://leetcode.cn/problems/maximum-product-of-three-numbers/

解法1: 排序, 将数组排好序然后算乘积即可
如果数组中全是正数或全是负数,则排序后最大的三个数相乘即为最大乘积;
如果数组中有正数有负数,则最大乘积既可能是三个最大正数的乘积,也可能是两个最小负数(即绝对值最大)与最大正数的乘积。
public int maximumProduct(int[] nums) {
Arrays.sort(nums);
int n = nums.length;
return Math.max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);
}
第二种解法: 利用5个变量找出, 最大的三个数以及最小的两个数
统计数组中的元素
645
https://leetcode.cn/problems/set-mismatch/
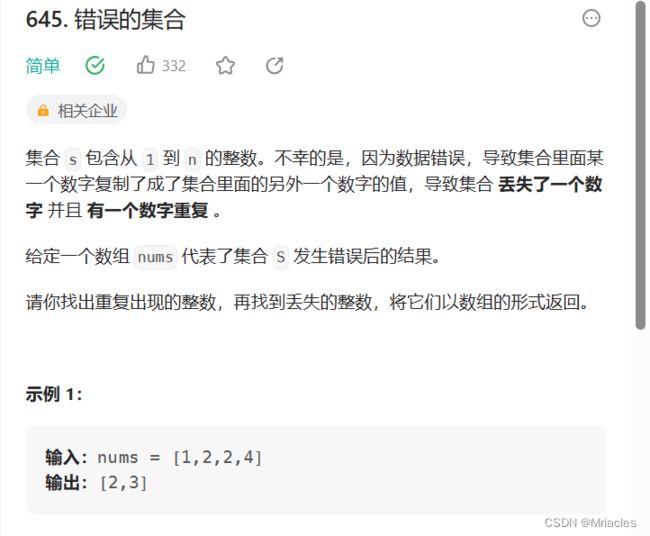
解法:该题型都是一种解法,就是将 i位置上的数 换成 i+1 的数, 这个是已经按这种规律弄好了的,所以我们直接找就行了,如果是无序的就需要我们遍历弄成这种结构
public int[] findErrorNums(int[] nums) {
int[] arr=new int[2];
for (int i = 0; i <= nums.length-1; i++) {
if (i+1 != nums[i]){
arr[0]=i;
arr[1]=i+1 > nums[i]?i+1:nums[i];
break;
}
}
return arr;
}
697
https://leetcode.cn/problems/degree-of-an-array/

题的意思就是: 包含最小度的连续子数组的长度是多少
暴力解法: 枚举所有可能性,然后得出最小连续子数组长度多少
解法1:利用哈希表来存放, 子数组的长度以及次数
public int findShortestSubArray(int[] nums) {
/*用的是Integer和数组定义的
* 0代表出现次数,1代表出现起始位置,2代表最终位置*/
Map<Integer, int[]> map = new HashMap<Integer, int[]>();
int n = nums.length;
for (int i = 0; i < n; i++) {
if (map.containsKey(nums[i])) {
map.get(nums[i])[0]++;
map.get(nums[i])[2] = i;
} else {
map.put(nums[i], new int[]{1, i, i});
}
}
int maxNum = 0, minLen = 0;
/*max代表最大次数,min最小长度*/
for (Map.Entry<Integer, int[]> entry : map.entrySet()) {
int[] arr = entry.getValue();
if (maxNum < arr[0]) {
maxNum = arr[0];
minLen = arr[2] - arr[1] + 1;
} else if (maxNum == arr[0]) {
if (minLen > arr[2] - arr[1] + 1) {
minLen = arr[2] - arr[1] + 1;
}
}
}
return minLen;
}
448
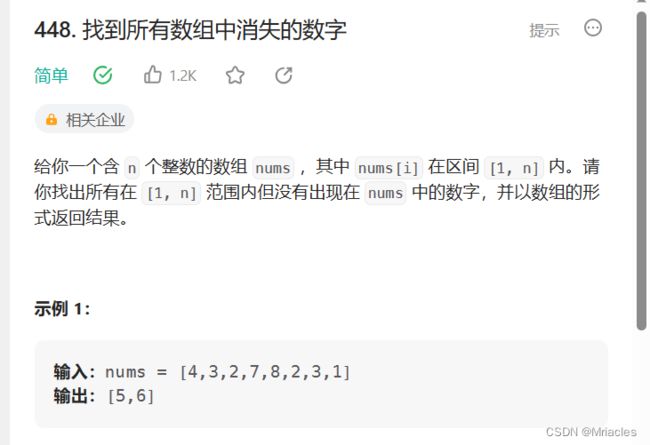
解法: 同样的让i位置上的数等于 i+1,不等的就是消失的数了
这个重点是下面的修改操作,建议背会
public static List<Integer> findDisappearedNumbers(int[] nums) {
List<Integer> list = new ArrayList<>();
for (int val:nums) {
modify(val,nums);
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] != i+1){
list.add(i+1);
}
}
return list;
}
private static void modify(int val, int[] arr) {
while (arr[val-1] != val){
int tmp = arr[val-1];
arr[val-1] = val;
val =tmp;
}
}
解法2:利用哈希表记录
public List<Integer> findDisappearedNumbers(int[] nums) {
List<Integer> list=new LinkedList<>();
HashMap<Integer,Integer> hashMap=new HashMap<>();
for (int i = 0; i < nums.length; i++) {
hashMap.put(nums[i],hashMap.getOrDefault(nums[i],0)+1);
}
for (int i = 1; i <= nums.length; i++) {
if (!hashMap.containsKey(i)){
list.add(i);
}
}
return list;
}
442

解法: nums[i] 加上「负号」表示数 i+1 已经出现过一次。具体地,我们首先对数组进行一次遍历。当遍历到位置 i 时,我们考虑 nums[nums[i]−1的正负性:
public List<Integer> findDuplicates(int[] nums) {
int n = nums.length;
List<Integer> ans = new ArrayList<Integer>();
for (int i = 0; i < n; ++i) {
int x = Math.abs(nums[i]);
if (nums[x - 1] > 0) {
nums[x - 1] = -nums[x - 1];
} else {
ans.add(x);
}
}
return ans;
}
41
 对数组进行一次遍历,对于遍历到的数 x=nums[i] 如果 x∈[1,N]我们就知道 x 应当出现在数组中的 x−1 的位置,因此交换 nums[i] 和 nums[x−1],这样 xxx 就出现在了正确的位置。在完成交换后,新的 nums[i]可能还在 [1,N]的范围内,我们需要继续进行交换操作,直到 x∉[1,N]
对数组进行一次遍历,对于遍历到的数 x=nums[i] 如果 x∈[1,N]我们就知道 x 应当出现在数组中的 x−1 的位置,因此交换 nums[i] 和 nums[x−1],这样 xxx 就出现在了正确的位置。在完成交换后,新的 nums[i]可能还在 [1,N]的范围内,我们需要继续进行交换操作,直到 x∉[1,N]
注意到上面的方法可能会陷入死循环。如果 nums[i] 恰好与 nums[x−1]\textit{nums}[x - 1]nums[x−1] 相等,那么就会无限交换下去。此时我们有 nums[i]=x=nums[x−1]说明 x 已经出现在了正确的位置。因此我们可以跳出循环,开始遍历下一个数。
解法:
public int firstMissingPositive(int[] nums) {
int n = nums.length;
for (int i = 0; i < n; ++i) {
while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
int temp = nums[nums[i] - 1];
nums[nums[i] - 1] = nums[i];
nums[i] = temp;
}
}
for (int i = 0; i < n; ++i) {
if (nums[i] != i + 1) {
return i + 1;
}
}
return n + 1;
}
数组的改变与移动
453

有一个规律叫做,正难反易 , 正面将数组加到一个相等的状况比较难, 所以我们考虑如何让数组减小到一个最小值
我们可以轻易得到, 每个数与相对最小值的次数,就是它的最小操作次数
public int minMoves(int[] nums) {
int minNum = Arrays.stream(nums).min().getAsInt();
int res = 0;
for (int num : nums) {
res += num - minNum;
}
return res;
}
665—
public boolean checkPossibility(int[] nums) {
int n = nums.length, cnt = 0;
for (int i = 0; i < n - 1; ++i) {
int x = nums[i], y = nums[i + 1];
if (x > y) {
cnt++;
if (cnt > 1) {
return false;
}
if (i > 0 && y < nums[i - 1]) {
nums[i + 1] = x;
}
}
}
return true;
}
283

解法: 利用双指针right是不等于0的数,每次遇到不等于的数就将这个数挪到前面
public void moveZeroes(int[] nums) {
int n = nums.length, left = 0, right = 0;
while (right < n) {
if (nums[right] != 0) {
swap(nums, left, right);
left++;
}
right++;
}
}
public void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
二维数组以及滚动数组
118
class Solution {
public List<List<Integer>> generate(int rowIndex) {
List<List<Integer>> C = new ArrayList<List<Integer>>();
for (int i = 0; i < rowIndex; ++i) {
List<Integer> row = new ArrayList<Integer>();
for (int j = 0; j <= i; ++j) {
if (j == 0 || j == i) {
row.add(1);
} else {
row.add(C.get(i - 1).get(j - 1) + C.get(i - 1).get(j));
}
}
C.add(row);
}
return C;
}
}
119
public List<Integer> getRow(int rowIndex) {
List<List<Integer>> C = new ArrayList<List<Integer>>();
for (int i = 0; i <= rowIndex; ++i) {
List<Integer> row = new ArrayList<Integer>();
for (int j = 0; j <= i; ++j) {
if (j == 0 || j == i) {
row.add(1);
} else {
row.add(C.get(i - 1).get(j - 1) + C.get(i - 1).get(j));
}
}
C.add(row);
}
return C.get(rowIndex);
}
661
public int[][] imageSmoother(int[][] img) {
int m = img.length, n = img[0].length;
int[][] ret = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int num = 0, sum = 0;
for (int x = i - 1; x <= i + 1; x++) {
for (int y = j - 1; y <= j + 1; y++) {
if (x >= 0 && x < m && y >= 0 && y < n) {
num++;
sum += img[x][y];
}
}
}
ret[i][j] = sum / num;
}
}
return ret;
}
第二种:利用前缀和的思想 ,求每个i位置的的和
二维前缀和模板

for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + arr[i][j];
public int[][] imageSmoother(int[][] img) {
int m = img.length, n = img[0].length;
int[][] sum = new int[m + 10][n + 10];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + img[i - 1][j - 1];
}
}
int[][] ans = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int a = Math.max(0, i - 1), b = Math.max(0, j - 1);
int c = Math.min(m - 1, i + 1), d = Math.min(n - 1, j + 1);
int cnt = (c - a + 1) * (d - b + 1);
int tot = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b];
ans[i][j] = tot / cnt;
}
}
return ans;
}
419—
class Solution {
static int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int m, n;
char[][] board;
boolean[][] visited;
public int countBattleships(char[][] board) {
int battleships = 0;
this.m = board.length;
this.n = board[0].length;
this.board = board;
this.visited = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == '.' || visited[i][j]) {
continue;
}
battleships++;
dfs(i, j);
}
}
return battleships;
}
public void dfs(int row, int col) {
visited[row][col] = true;
for (int[] dir : dirs) {
int newRow = row + dir[0], newCol = col + dir[1];
if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && board[newRow][newCol] == 'X' && !visited[newRow][newCol]) {
dfs(newRow, newCol);
}
}
}
}
数组的旋转
189
public void rotate(int[] nums, int k) {
int n = nums.length;
int[] newArr = Arrays.copyOf(nums,nums.length);
for (int i = 0; i < n; ++i) {
nums[(i + k) % n] = newArr[i];
}
}
396
class Solution {
public int maxRotateFunction(int[] nums) {
int f = 0, n = nums.length, numSum = Arrays.stream(nums).sum();
for (int i = 0; i < n; i++) {
f += i * nums[i];
}
int res = f;
for (int i = n - 1; i > 0; i--) {
f += numSum - n * nums[i];
res = Math.max(res, f);
}
return res;
}
}
特定顺序遍历二维数组
54

解法: 用特定的黑盒来遍历一个框架,每次传过去一个框架就行了
public List<Integer> spiralOrder(int[][] matrix) {
int x1 =0 ,y1=0;
int x2 =matrix.length-1,y2=matrix[0].length-1;
List<Integer> list = new ArrayList<>();
while (x1 <= x2 && y1 <= y2){
process1(matrix,x1,y1,x2,y2,list);
x1++;y1++;
x2--;y2--;
}
return list;
}
private static void process1(int[][] arr, int x1,int y1,int x2, int y2,List<Integer> list){
for (int i = y1; i <= y2; i++) {
list.add(arr[x1][i]);
}
for (int i = x1+1; i <= x2; i++) {
list.add(arr[i][y2]);
}
// 最后俩个要注意一下细节问题, 因为如果行与列不一致的话,很可能会重复,要进过判断去重
for (int i = y2-1; i >= y1&& x1 != x2; i--) {
list.add(arr[x2][i]);
}
for (int i = x2-1; i > x1 && y1 != y2; i--) {
list.add(arr[i][y1]);
}
}
59
public int[][] generateMatrix(int n) {
if (n <= 0){
return null;
}
int[][] array=new int[n][n];
int left = 0;
int right = n-1;
int top = 0;
int bottom = n-1;
int numEle = 1;
while (numEle <= n*n){
for (int i = left; i <= right && numEle <= n*n; i++) {
array[top][i]=numEle;
numEle++;
}
top++;
for (int i = top; i <= bottom && numEle <= n*n ; i++) {
array[i][right]=numEle;
numEle++;
}
right--;
for (int i = right; i >= left && numEle <= n*n; i--) {
array[bottom][i]=numEle;
numEle++;
}
bottom--;
for (int i = bottom; i >= top && numEle <= n*n; i--) {
array[i][left]=numEle;
numEle++;
}
left++;
}
return array;
}
498
// // 斜的方式打印
public static void printMatrZigzag(int[][] arr){
int ar=0,ac=0,br=0,bc=0;
int endR = arr.length-1;
int endC = arr[0].length-1;
boolean from = false;
while (ar != endR+1){
printLevel(arr,ar,ac,br,bc,from);
ar=ac == endC?ar+1:ar;// a到了最后一列 a的行才增加
ac= ac == endC?ac:ac+1;// a的列到了最后一列才不变, 否则就增加
bc = br == endR?bc+1:bc;
br =br == endR?br:br+1;
from =!from;
}
System.out.println();
}
private static void printLevel(int[][] arr, int tr, int tc, int dr, int dc, boolean from) {
if (from){
while (tr != dr+1) System.out.println(arr[tr++][tc--]+" ");
}else {
while (dr != tr-1){
System.out.println(arr[dr--][dc++]+" ");
}
}
}
二维数组的变换
566
class Solution {
public int[][] matrixReshape(int[][] nums, int r, int c) {
int m = nums.length;
int n = nums[0].length;
if (m * n != r * c) {
return nums;
}
int[][] ans = new int[r][c];
for (int x = 0; x < m * n; ++x) {
ans[x / c][x % c] = nums[x / n][x % n];
}
return ans;
}
}
48
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < (n + 1) / 2; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
}
}
73—

解法: 先判断第一行和第一列有没有0,然后用其他列来处理第一行和第一列,最后更新第一行和第一列
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
boolean flagCol0 = false, flagRow0 = false;
for (int i = 0; i < m; i++) {
if (matrix[i][0] == 0) {
flagCol0 = true;
}
}
for (int j = 0; j < n; j++) {
if (matrix[0][j] == 0) {
flagRow0 = true;
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = matrix[0][j] = 0;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
if (flagCol0) {
for (int i = 0; i < m; i++) {
matrix[i][0] = 0;
}
}
if (flagRow0) {
for (int j = 0; j < n; j++) {
matrix[0][j] = 0;
}
}
}
}
前缀和数组
前缀和思想 - 快速求出数组中某一段连续区间的和
第一步: 先预处理来一个前缀和数组
dp[i]表示[1,i]所有元素的和
第二部: 求某一段的和就是用大的长度减去小的长度


import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int q = in.nextInt();
int[][] arr = new int[n + 1][m + 1];
long[][] dp = new long[n + 1][m + 1];
// 读⼊数据
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
arr[i][j] = in.nextInt();
// 处理前缀和矩阵
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + arr[i][j];
while(q > 0)
{
int x1 = in.nextInt(), y1 = in.nextInt(), x2 = in.nextInt(), y2 = in.nextInt();
System.out.println(dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]);
q--;
}
}
}
303
import java.util.*;
class NumArray {
int[] array=null;
public NumArray(int[] nums) {
array= Arrays.copyOf(nums,nums.length);
}
public int sumRange(int left, int right) {
int sum=0;
for (int i = left; i <= right; i++) {
sum+=array[i];
}
return sum;
}
}
238
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] pre = new int[n];
int[] post = new int[n];
// 细节问题 首尾是 1 不是 0
post[n-1] = 1;pre[0]=1;
for(int i =1 ;i < n;i++){
pre[i]=pre[i-1]*nums[i-1];
}
for(int i = n-2 ; i >= 0 ;i-- ){
post[i] = post[i+1]*nums[i+1];
}
int[] ans = new int[n];
for(int i=0;i < n ; i++){
ans[i] = pre[i]*post[i];
}
return ans;
}
}
506
public int subarraySum(int[] nums, int k) {
int sum =0;
HashMap<Integer,Integer> map = new HashMap<>();
map.put(0,1);
int ret=0;
for(int i =0;i< nums.length;i++){
sum+= nums[i];
ret+=map.getOrDefault(sum-k,0);
map.put(sum,map.getOrDefault(sum,0)+1);
}
return ret;
}

同余定理: 如果 (a - b) % n == 0 ,那么我们可以得到⼀个结论: a % n == b % n
如果出现负数情况下:怎么修正

public int subarraysDivByK(int[] nums, int k) {
int sum=0,ret=0;
Map<Integer,Integer> map = new HashMap<>();
map.put(0%k,1);
for (int i = 0; i < nums.length; i++) {
sum+=nums[i];
int r = (sum%k+k)%k;
ret+=map.getOrDefault(r,0);
map.put(r,map.getOrDefault(r,0)+1);
}
return ret;
}