【优选算法】—— 滑动窗口类问题

本期，我给大家带来的是关于滑动窗口类算法的介绍，并通过具体的题目帮助大家思考理解。

 

 

目录

（一）基本概念

（二）题目讲解

1、难度：medium

1️⃣长度最小的子数组

2️⃣找到字符串中所有字⺟异位词

2、难度：hard

1️⃣最⼩覆盖⼦串

2️⃣串联所有单词的⼦串

总结

---

（一）基本概念

滑动窗口算法（Sliding Window Algorithm）是一种常见的算法技巧，用于解决一些数组或字符串相关的问题。该算法基于窗口的概念，在一个固定大小的窗口内移动，并根据具体问题进行适当的调整和计算。

下面将详细的介绍滑动窗口算法的工作原理和应用场景：

工作原理：

• 窗口大小：滑动窗口算法通过设定一个窗口的大小来解决问题。窗口通常是一个连续的子数组或子字符串。
• 初始化窗口：初始化窗口的起始位置，并根据问题需求设定窗口的大小。
• 移动窗口：通过移动窗口的起始位置，不断调整窗口的大小和位置，以找到满足问题条件的解。
• 更新解：根据窗口的移动和调整，更新问题的解，并记录或返回所需的结果。

应用场景：

• 最小/最大子数组/子字符串：寻找给定数组或字符串中满足特定条件的最小或最大的子数组或子字符串。
• 字符串匹配：在一个字符串中寻找另一个字符串的出现或满足特定条件的子串。
• 滑动窗口和哈希表结合：通过使用哈希表来优化滑动窗口算法，提高效率。
• 优化窗口大小：根据问题的特性，调整窗口大小以寻找最佳解。

滑动窗口算法的步骤通常如下：

1. 初始化窗口的起始位置和结束位置，使其满足问题的要求。
2. 进入循环，不断移动窗口的起始位置和结束位置，直到窗口滑动到数组或字符串的末尾。
3. 在每一次循环中，检查窗口内的元素是否满足问题的要求。如果满足条件，则更新解或执行其他操作。如果不满足条件，则继续移动窗口。
4. 在移动窗口时，要更新窗口内的元素和相应的数据结构，以确保窗口的正确性。
5. 重复步骤2到步骤4，直到遍历完整个数组或字符串，返回解或所需的结果。

---

（二）题目讲解

接下来，我们通过几道题目让大家具体的感受一下。（题目由易到难）

1、难度：medium

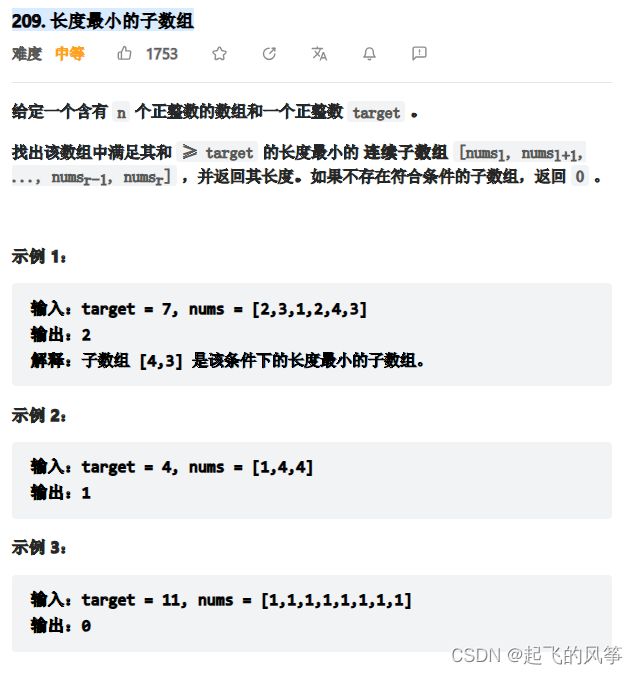
1️⃣长度最小的子数组

题⽬链接：209. 长度最小的子数组

 【题⽬描述】

【解法】（滑动窗⼝）

算法思路：
由于此问题分析的对象是「⼀段连续的区间」，因此可以考虑「滑动窗」的思想来解决这道题。
让滑动窗⼝满⾜：从 i 位置开始，窗⼝内所有元素的和⼩于target （那么当窗内元素之和
第⼀次⼤于等于⽬标值的时候，就是 i 位置开始，满⾜条件的最⼩⻓度）。

做法：将右端元素划⼊窗⼝中，统计出此时窗⼝内元素的和：

• 如果窗⼝内元素之和⼤于等于 target ：更新结果，并且将左端元素划出去的同时继续判断是否满⾜条件并更新结果（因为左端元素可能很⼩，划出去之后依旧满⾜条件）
• 如果窗⼝内元素之和不满⾜条件： right++ ，另下⼀个元素进⼊窗⼝。
   

【原理解释】

很多题解以及帖⼦只给你说怎么做，没给你解释为什么这么做。即为何滑动窗⼝可以解决问题，并且时间复杂度更低？

▪ 这个窗⼝寻找的是：以当前窗⼝最左侧元素（记为 left1 ）为基准，符合条件的情况。也
就是在这道题中，从 left1 开始，满⾜区间和 sum >= target 时的最右侧（记为
right1 ）能到哪⾥。

▪ 我们既然已经找到从 left1 开始的最优的区间，那么就可以⼤胆舍去 left1 。但是如
果此时重新开始统计第⼆个元素（ left2 ）往后的和，势必会有⼤量重复的计算（因为我们在求第⼀段区间的时候，已经算出很多元素的和了，这些和是可以在计算下次区间和的时候⽤上的）。

▪ 此时， rigth1 的作⽤就体现出来了，我们只需将 left1 这个值从 sum 中剔除。从
right1 这个元素开始，往后找满⾜ left2 元素的区间（此时 right1 也有可能是满⾜的，因为 left1 可能很⼩。 sum 剔除掉 left1 之后，依旧满⾜⼤于等于target ）。这样我们就能省掉⼤量重复的计算。

▪ 这样我们不仅能解决问题，⽽且效率也会⼤⼤提升
 

【算法实现】

class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int n = nums.size(), sum = 0, len = INT_MAX;
        for(int left = 0, right = 0; right < n; right++)
        {
            sum += nums[right]; // 进窗⼝
            while(sum >= target) // 判断
            {
                len = min(len, right - left + 1); // 更新结果
                sum -= nums[left++]; // 出窗⼝
            }
        }
    return len == INT_MAX ? 0 : len;
    }
};

【结果展示】

 【性能分析】

 具体的性能分析如下：

• 时间复杂度：因为每个元素最多被遍历两次（进窗口和出窗口），时间复杂度是线性的。所以时间复杂度为O(n)，其中n是数组nums的长度。
• 空间复杂度：代码中只使用了几个额外的变量，不随输入规模变化，所以空间复杂度为O(1)。

---

 

2️⃣找到字符串中所有字⺟异位词

题⽬链接：438. 找到字符串中所有字母异位词

 

【题⽬描述】

【解法】（滑动窗⼝+ 哈希表）

算法思路：

1. 因为字符串 p 的异位词的⻓度⼀定与字符串 p 的⻓度相同，所以我们可以在字符串 s 中构造⼀个⻓度为与字符串 p 的⻓度相同的滑动窗⼝，并在滑动中维护窗⼝中每种字⺟的数量；
2. 当窗⼝中每种字⺟的数量与字符串 p 中每种字⺟的数量相同时，则说明当前窗⼝为字符串 p 的异位词；
3.  因此可以⽤两个⼤⼩为 26 的数组来模拟哈希表，⼀个来保存 s 中的⼦串每个字符出现的个数，另⼀个来保存 p 中每⼀个字符出现的个数。这样就能判断两个串是否是异位词。

【算法实现】

class Solution {
public:
    vector findAnagrams(string s, string p) {
        vector ret;
        int hash1[26] = { 0 }; // 统计字符串 p 中每个字符出现的个数
        for(auto ch : p) 
            hash1[ch - 'a']++;
        int hash2[26] = { 0 }; // 统计窗⼝⾥⾯的每⼀个字符出现的个数
        int m = p.size();
        for(int left = 0, right = 0, count = 0; right < s.size(); right++)
        {
            char in = s[right];
            // 进窗⼝ + 维护 count
            if(++hash2[in - 'a'] <= hash1[in - 'a']) 
                count++;
            if(right - left + 1 > m) // 判断
            {
                char out = s[left++];
                // 出窗⼝ + 维护 count
                if(hash2[out - 'a']-- <= hash1[out - 'a']) 
                    count--;
            }
            // 更新结果
            if(count == m) 
                ret.push_back(left);
        }
        return ret;
    }
};

【结果展示】

 【性能分析】

具体的性能分析如下：

• 时间复杂度：代码中使用了双指针来遍历字符串s，所以时间复杂度为O(n)，其中n是字符串s的长度。
• 空间复杂度：代码中使用了两个大小为26的哈希数组，所以空间复杂度为O(1)。

---

2、难度：hard

1️⃣最⼩覆盖⼦串

链接如下：76. 最小覆盖子串

【题⽬描述】

 

【解法】 （滑动窗⼝+哈希表）

算法思路：
◦ 研究对象是连续的区间，因此可以尝试使⽤滑动窗⼝的思想来解决。
◦ 如何判断当前窗⼝内的所有字符是符合要求的呢？

• 我们可以使⽤两个哈希表，其中⼀个将⽬标串的信息统计起来，另⼀个哈希表动态的维护窗⼝内字符串的信息。
• 当动态哈希表中包含⽬标串中所有的字符，并且对应的个数都不⼩于⽬标串的哈希表中各个字符的个数，那么当前的窗⼝就是⼀种可⾏的⽅案

【算法流程】

a. 定义两个全局的哈希表： 1 号哈希表 hash1 ⽤来记录⼦串的信息， 2 号哈希表 hash2 ⽤来记录⽬标串 t 的信息；

b.  实现⼀个接⼝函数，判断当前窗⼝是否满⾜要求：
    i. 遍历两个哈希表中对应位置的元素：
        • 如果 t 中某个字符的数量⼤于窗⼝中字符的数量，也就是 2 号哈希表某个位置⼤于1 号哈希表。说明不匹配，返回 false ；
        • 如果全都匹配，返回 true

主函数中：
a. 先将 t 的信息放⼊ 2 号哈希表中；
b. 初始化⼀些变量：左右指针： left = 0，right = 0 ；⽬标⼦串的⻓度： len =
INT_MAX ；⽬标⼦串的起始位置： retleft ；（通过⽬标⼦串的起始位置和⻓度，我们就
能找到结果）
c. 当 right ⼩于字符串 s 的⻓度时，⼀直下列循环：

• i. 将当前遍历到的元素扔进 1 号哈希表中；
• ii. 检测当前窗⼝是否满⾜条件：

• 如果满⾜条件：
        ◦ 判断当前窗⼝是否变⼩。如果变⼩：更新⻓度 len ，以及字符串的起始位置
retleft ；
        ◦ 判断完毕后，将左侧元素滑出窗⼝，顺便更新 1 号哈希表；
        ◦ 重复上⾯两个过程，直到窗⼝不满⾜条件；

• iii. right++ ，遍历下⼀个元素；

d. 判断 len 的⻓度是否等于 INT_MAX ：

• i. 如果相等，说明没有匹配，返回空串；
• ii. 如果不想等，说明匹配，返回 s 中从 retleft 位置往后 len ⻓度的字符串。

【算法实现】

class Solution {
public:
    string minWindow(string s, string t) {
        int hash1[128] = { 0 }; // 统计字符串 t 中每⼀个字符的频次
        int kinds = 0; // 统计有效字符有多少种
        for(auto ch : t)
        if(hash1[ch]++ == 0) kinds++;
        int hash2[128] = { 0 }; // 统计窗⼝内每个字符的频次
        int minlen = INT_MAX, begin = -1;
        for(int left = 0, right = 0, count = 0; right < s.size(); right++)
        {
            char in = s[right];
            if(++hash2[in] == hash1[in]) count++; // 进窗⼝ + 维护 count
            while(count == kinds) // 判断条件
            {
                if(right - left + 1 < minlen) // 更新结果
                {
                    minlen = right - left + 1;
                    begin = left;
                }
                char out = s[left++];
                if(hash2[out]-- == hash1[out]) count--; // 出窗⼝ + 维护 count
            }
        }
        if(begin == -1) 
            return "";
        else 
            return s.substr(begin, minlen);
    }
};

【结果展示】

 

【性能分析】

具体的性能分析如下：

• 时间复杂度：算法的时间复杂度为O(n)，n为字符串s的长度。代码使用哈希表记录频次信息，实现了线性时间复杂度。

• 空间复杂度：哈希表hash1和hash2的存储空间为128个元素的数组，因此空间复杂度为O(1)。

---

2️⃣串联所有单词的⼦串

链接如下：30. 串联所有单词的子串

【题⽬描述】

 

 【解法】

算法思路：

如果我们把每⼀个单词看成⼀个⼀个字⺟，问题就变成了找到「字符串中所有的字⺟异位词」。⽆
⾮就是之前处理的对象是⼀个⼀个的字符，我们这⾥处理的对象是⼀个⼀个的单词。
 

因此，这道题就留给大家自己做了！！

---

总结

以上就是本期关于滑动窗口算法的主要内容讲解了。感谢大家的观看与支持！！！