数据结构--树和森林的遍历
数据结构–树和森林的遍历
树的先根遍历
void PreOrder(TreeNode* R)
{
if (R != NULL)
{
visit(R);
while (R还有下一个子树T)
PreOrder(T);
}
}
树和二叉树的转化后==》
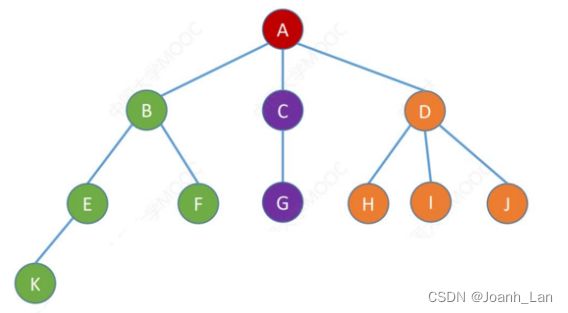
树的先根遍历序列与这棵树相应二叉树的先序序列相同。 \color{red}树的先根遍历序列与这棵树相应二叉树的先序序列相同。 树的先根遍历序列与这棵树相应二叉树的先序序列相同。
A B C D A ( B E F ) ( C G ) ( D H I ) A ( B ( E , K ) F ) ( C G ) ( D H I J ) \begin{array}{ccccccccc}\mathbf{A}&\mathbf{B}&&\mathbf{C}&&\mathbf{D}&\\\mathbf{A}&(\mathbf{B}&\mathbf{E}&\mathbf{F})&(\mathbf{C}&\mathbf{G})&(\mathbf{D}&\mathbf{H}&\mathbf{I})\\\mathbf{A}&(\mathbf{B}&(\mathbf{E},\mathbf{K})&\mathbf{F})&(\mathbf{C}&\mathbf{G})&(\mathbf{D}&\mathbf{H}&\mathbf{I}&\mathbf{J})\end{array} AAAB(B(BE(E,K)CF)F)(C(CDG)G)(D(DHHI)IJ)
树的后根遍历
void PreOrder(TreeNode* R)
{
if (R != NULL)
{
while (R还有下一个子树T)
PreOrder(T);
visit(R);
}
}
树和二叉树的转化后==》
树的后根遍历序列与这棵树相应二叉树的中序序列相同。 \color{red}树的后根遍历序列与这棵树相应二叉树的中序序列相同。 树的后根遍历序列与这棵树相应二叉树的中序序列相同。
B C D A ( E F B ) ( G C ) ( H I J D ) A ( ( K E ) F B ) ( G C ) ( H I J D ) A \begin{array}{cccccccc}&&\text{B}&\text{C}&&&\text{D}&\text{A}\\(&\mathrm{E}&\mathrm{F}&\mathrm{B})&(\mathrm{G}&\mathrm{C})&(\mathrm{H}&\mathrm{I}&\mathrm{J}&\mathrm{D})&\mathrm{A}\\((\mathrm{K}&\mathrm{E})&\mathrm{F}&\mathrm{B})&(\mathrm{G}&\mathrm{C})&(\mathrm{H}&\mathrm{I}&\mathrm{J}&\mathrm{D})&\mathrm{A}\end{array} (((KEE)BFFCB)B)(G(GC)C)D(H(HAIIJJD)D)AA
树的层次遍历
广度优先遍历 \color{green}广度优先遍历 广度优先遍历
3) 层次遍历 \color{red}层次遍历 层次遍历(用队列实现)
①若树非空,则根节点入队
②若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队
③重复②直到队列为空
森林的先序遍历
森林。森林是 m ( m ≥ 0 ) m (m\ge0) m(m≥0)棵互不相交的树的集合。每棵树去掉根节点后,其各个子树又组成森林。
1) 先序遍历森林 \color{red}先序遍历森林 先序遍历森林。
若森林为非空,则按如下规则进行遍历:
访问森林中第一棵树的根结点。
先序遍历第一棵树中根结点的子树森林。
先序遍历除去第一棵树之后剩余的树构成的森林。
效果等同于依次对各个树进行先根遍历 \color{red}效果等同于依次对各个树进行先根遍历 效果等同于依次对各个树进行先根遍历
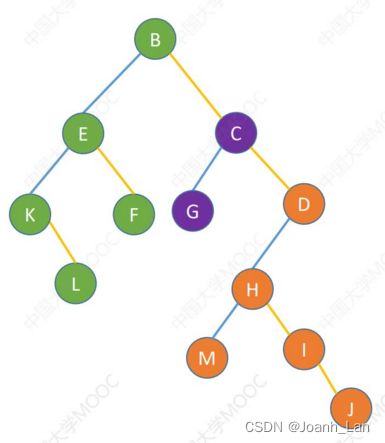
BCD ( B E F ) ( C G ) ( D H I J ) (B(EKL) F) (C G) (D (H M) I J) \begin{aligned} &\text{BCD} \\ &(BEF)(CG)(DHIJ) \\ &\text{(B(EKL) F) (C G) (D (H M) I J)} \end{aligned} BCD(BEF)(CG)(DHIJ)(B(EKL) F) (C G) (D (H M) I J)
效果等同于依次对二叉树的先序遍历 \color{red}效果等同于依次对二叉树的先序遍历 效果等同于依次对二叉树的先序遍历
森林的中序遍历
森林。森林是 m ( m ≥ 0 ) m (m\ge0) m(m≥0)棵互不相交的树的集合。每棵树去掉根节点后,其各个子树又组成森林。
2) 中序遍历森林 \color{red}中序遍历森林 中序遍历森林。
若森林为非空,则按如下规则进行遍历:
中序遍历森林中第一棵树的根结点的子树森林。访问第一棵树的根结点。
中序遍历除去第一棵树之后剩余的树构成的森林。
效果等同于依次对各个树进行后根遍历 \color{red}效果等同于依次对各个树进行后根遍历 效果等同于依次对各个树进行后根遍历
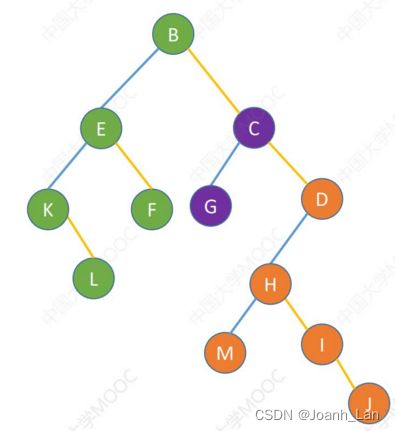
B C D ( E F B ) ( G C ) ( H J D ) ( ( K L E ) F B ) ( G C ) ( ( M H ) I J D ) \begin{array}{cccccccc}&&&&\text{B}&&\text{C}&&\text{D}\\(&&&E&\text{F}&\text{B})&(\text{G}&\text{C})&(&\text{H}&\text{J}&\text{D})\\((\text{K}&\text{L}&\text{E})&\text{F}&\text{B})&(\text{G}&\text{C})&((\text{M}&\text{H})&\text{I}&\text{J}&\text{D})\end{array} (((KLE)EFBFB)B)(GC(GC)C)((MD(H)HIJJD)D)
效果等同于依次对二叉树的中序遍历 \color{red}效果等同于依次对二叉树的中序遍历 效果等同于依次对二叉树的中序遍历