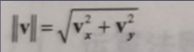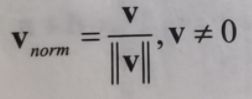1.2 向量基础

什么是向量
向量的定义
①向量是有大小和方向的有向线段。
②向量没有位置，只有大小和方向
③向量的箭头是向量的结束，尾是向量的开始
④向量魔术的位移能被认为是宇宙平行的唯一序列
（向量的数组不是向量的位置，而是向量在各个维度上的位移长度）
⑤向量表示：三维（ax，by，zw） 二维（ax，by）

 

向量与标量
向量：有大小和方向的有向线段。
标量：只有大小，没有方向的量。
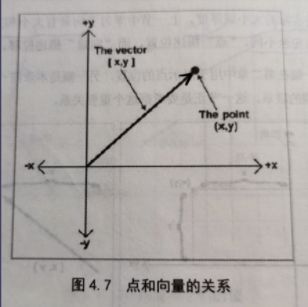
向量与点
向量和点，数学形式上相等，但几何意义完全不同。
点：有位置，没有实际大小和方向。
向量：无位置，有实际大小和方向。
联系：任何一个点都可以看做是从原点出发的向量。

零向量
①零向量是唯一大小为零的向量
②零向量是唯一一个没有方向的量
③零向量不是一个点，因为没有定义某个位置
④零向量表示没有位移，就像零标量表示没有数量一样
如何计算
标量与向量的计算
①不可加
②不可减
③乘法：将每个分量都与标量相乘就可以
④除法：等同于乘以标量的倒数
例：-2（2，-5） = （-4，-10）
例：（6，-2，-4）/ 2 = （3，-1，-2）
⑤几何解释：向量乘以标量的效果是以标量的大小缩放向量的长度，负值方向相反（将向量缩放至k个标量单位）

向量的模长
计算公式：

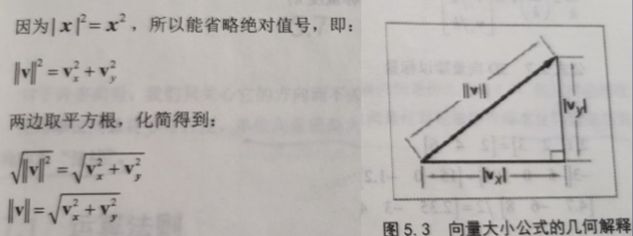
几何解释：如图所示，当我们将所示向量作为斜边构建成一个直角三角形，所示向量的大小（模长）即可通过三角形勾股定理推出。

例：（-12,5）的模长：sqr（pow（-12，2）+pow（5，2），0.5） = sqr（144+25，0.5）= 13
标准化向量
表转化向量（单位向量）就是大小为1的向量。
（适用范围：仅需要指导方向而不关心其大小。如：法线）
运算法则：将向量除以它的大小（模长）。

例：标准化向量（12,-5）

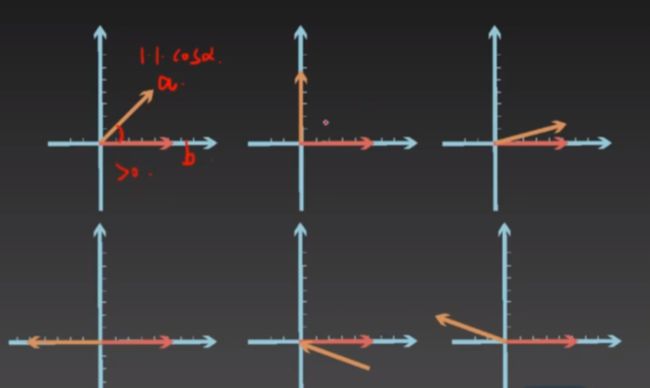
向量与向量的加减法计算
计算公式：（ax，ay）+（bx，by）=（ax + bx，ay + by）
加法：对应位置相加 例：（1,-4）+（7,5）=（8,1）
减法：对应位置相减 例：（-3,6）-（-4,3）=（1,3）PPT里面的（7,3）写错了
几何解释：
假设有向量（ax,bx）和向量（ay，by）

计算两点间距离：距离公式
计算公式：

应用范围：计算一个了向量到另一个向量的距离（a到b的位移向量为b-a）
几何解释：

向量的点积计算
点积又称点乘、内积
计算公式：（ax，ay）·（bx，by） = （axby+ayby）
例如：(-2,-5,-4)·(-4,1,0)=(-2)(-4)+(5)(1)+(-4)(0)=13
a·b=|a||b|cosΘ
向量点乘就是分量乘积的和，结果是一个标量并满足交换律ab=ba
几何解释：点积描述了两个向量方向的“相似”程度，点积结果越大，夹角越小，两个向量越接近（反馈到渲染上就是面的明暗程度）

向量投影（重要）
投影的几何解释：假设有两个向量V和n，将V分解为两个向量：V∥和V⊥，V∥平行于n，垂直于n，并满足V=V∥+V⊥。则平行分量V∥为V在n上的投影。（解释：一个向量在另一个向量上的投影长度）

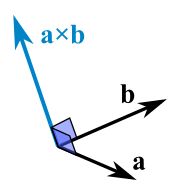
向量叉积计算
叉积又称叉乘。两个矢量的叉积 a × b 是与这两个矢量垂直的 矢量

计算公式：a × b = |a| |b| sin(θ) n
○|a|是矢量a的量值（长度）
○|b|是矢量b的量值（长度）
○θ 是a和b之间的角度
○n是与a和b垂直的单位矢量（向量）

长度是：a的长度乘以b的长度乘以a和b之间的角的正弦，然后乘以矢量n来确保结果是指着正确的方向（垂直于a和b）
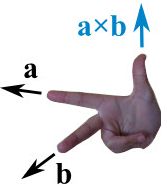
方向判定：若叉积指着相反的方向，它仍然垂直于相乘的两个矢量，需遵循“右手定则”
把食指指着矢量a的方向，把中指指着矢量b的方向：拇指指着的便是叉积的方向

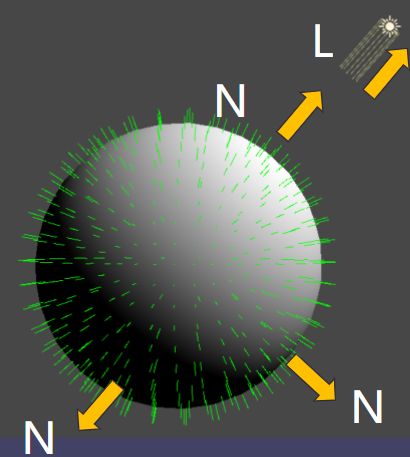
兰伯特光照模型
兰伯特光照模型是目前最简单通用的模型漫反射光照模型
是光照方向的反方向为L（light）向量，发现方向为N（normal）向量，则有：
L与N方向相同 则Normal·Light=1（纯亮）
L与N方向相反 则Normal·Light=-1（纯黑）
L与N方向垂直 则Normal·Light=0（纯黑）

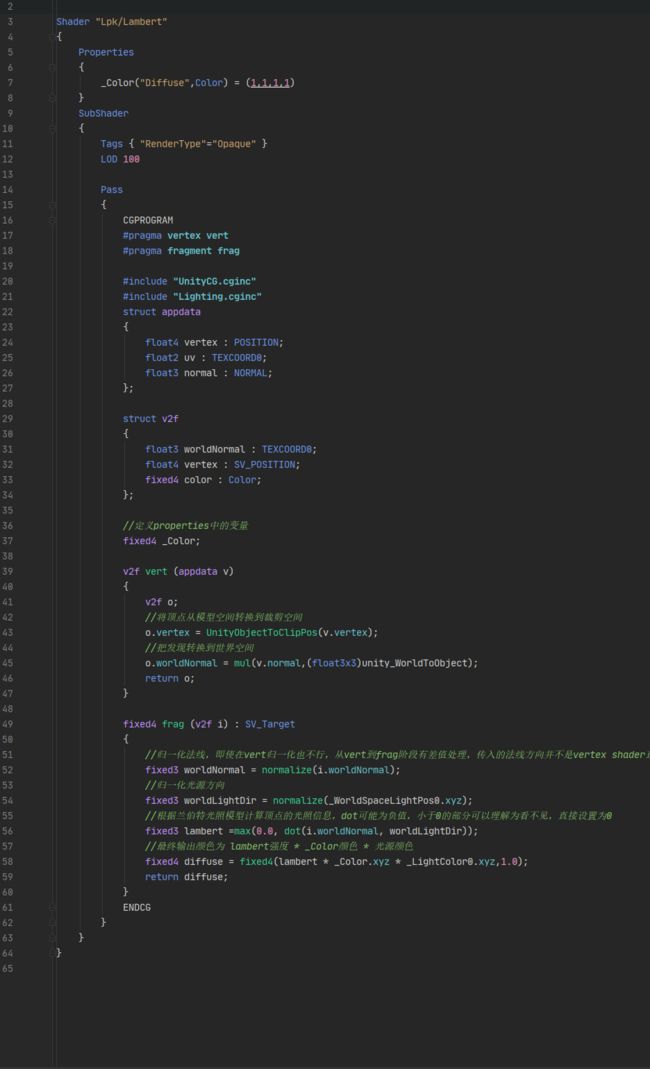
built-in下的兰伯特光照模型

若有收获，就点个赞吧

小电脑