王道数据结构精简笔记——顺序表(附完整工程)
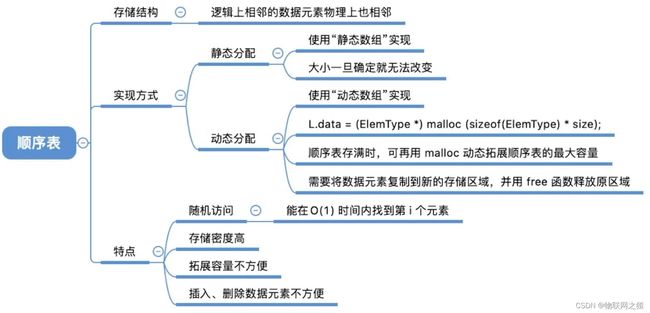
一、顺序表的定义
顺序表——用顺序存储的方式实现线性表。(逻辑相邻——>物理相邻)
1. 顺序表的实现——静态分配
#define MaxSize 10 //定义最大长度
typedef struct{
ElemType data[MaxSize]; // 用静态的“数组”存放数据元素
int length; // 顺序表的当前长度
}SqList; // 顺序表的类型定义(静态分配方式)
完整例子:
#include 2. 顺序表的实现——动态分配
#define InitSize 10 // 顺序表的初始长度
typedef struct{
ElemType *data; // 指示动态分配数组的指针
int MaxSize; // 顺序表的最大容量
int length; // 顺序表的当前长度
}SeqList; // 顺序表的类型定义(动态分配方式)
完整例子:
#include 顺序表特点:
- 随机访问
- 存储密度高
- 拓展容量不方便
- 插入、删除操作不方便
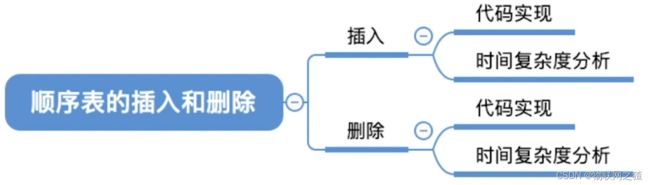
二、顺序表的插入删除(静态分配为例)
1. ListInsert(&L, i, e)
插入操作,在表L中的第i个位置上插入制定元素e。
#include 算法强壮性:
- 插入位序i应该在
1到length+1之间 - 当前长度是否会超过最大长度
用bool函数实现(bool的返回值要么是true要么是false)
bool ListInsert(SqList &L, int i, int e){
if (i < 1 || i > L.length + 1) // 判断i的范围是否有效
return false;
if (L.length >= MaxSize) // 当前存储空间已满,不能插入
return false;
for (int j = L.length; j >= i; j--) // 将第i个元素及之后元素后移
L.data[j] = L.data[j - 1];
L.data[i - 1] = e; // 在位置i处放入e
L.length++; // 长度+1
return true;
}
时间复杂度分析:
- 最好情况:新元素插入到表尾,i=n+1,循环0次;最好时间复杂度=O(1)
- 最坏情况:新元素插入到表头,i=1,循环n次;最坏时间复杂度=O(n)
- 平均情况:假设新元素插入到任何一个位置的概率相同,则平均循环次数=
n p + ( n − 1 ) p + ( n − 2 ) p + . . . . . . + 1 ⋅ p = [ n ( n + 1 ) / 2 ] ⋅ [ 1 / n + 1 ] = n / 2 np+(n-1)p+(n-2)p+......+1·p=[n(n+1)/2]·[1/n+1]=n/2 np+(n−1)p+(n−2)p+......+1⋅p=[n(n+1)/2]⋅[1/n+1]=n/2
平均时间复杂度=O(n/2)=O(n)
2. ListDelete(&L, i, &e)
删除操作,删除表L中的第i个位置的元素,并用e返回删除元素的值。
代码实现:
bool ListDelete(SqList &L, int i, int &e){
if(i < 1 || i > L.length) // 判断i的范围是否有效
return false;
e = L.data[i - 1]; // 将被删除的元素复制给e
for(int j = i; j < L.length; j++) // 将第i个位置后的元素前移
L.data[j - 1] = L.data[j];
L.length--; // 线性表长度-1
return true;
}
时间复杂度分析:
- 最好情况:删除表位元素,i=n,循环0次;最好时间复杂度=O(1)
- 最坏情况:删除表头元素,i=1,循环n-1次;最坏时间复杂度=O(n)
- 平均情况:假设删除任何一个元素的概率相同,平均循环次数为(n-1)/2,平均时间复杂度=O(n)
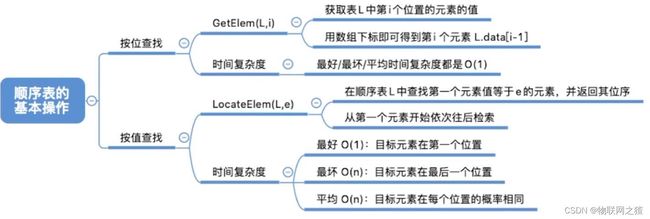
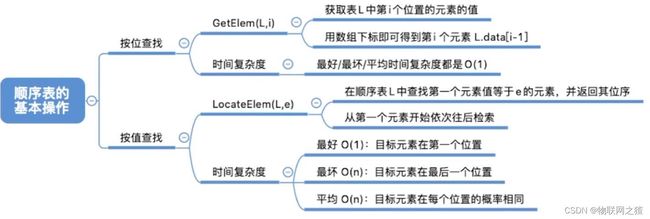
三、顺序表查找
1. GetElem(L, i)
按位查找操作。获取表L中第i个位置的元素的值。
ElemType GetElem(SqList L, int i){
return L.data[i - 1];
}
时间复杂度:O(1)
2. LocateElem(L, e)
按值查找操作。在表L中查找具有给定关键字值的元素。
int LocateElem(SeqList L, ElemType e){
for(int i = 0; i < L.length; i++)
if(L.data[i] == e)
return i + 1;
return 0;
}
时间复杂度:
- 最好情况:目标元素在表头,循环1次;最好时间复杂度=O(1)
- 最坏情况:目标元素在表尾,循环n次;最坏时间复杂度=O(n)
- 平均情况:假设目标元素出现在任何一个位置的概率都相同,平均循环次数为(n+1)/2;平均时间复杂度=O(n)
整合代码示例
#include